定積分の概要の確認|定積分と積分の応用を把握する #1

上記シリーズで積分の計算について取り扱いましたが、不定積分を中心に積分演算を確認しました。どちらかというと式変形に重きを置きましたが、長さや面積、体積などの計算や、確率分布の正規化など、積分の応用について考えるにあたっては定積分も把握すると良いです。
そこで当シリーズでは、主に定積分を用いた積分の応用について確認を行います。どちらかというと応用例に重きをおいて確認を行えればと思います。
#1では基本事項の確認にあたって、定積分の演算の概要について簡単に確認します。
以下目次になります。
1. 定積分と面積
2. 定積分と符号
3. まとめ
1. 定積分と面積
1節では「定積分と面積」について取り扱います。まず具体的に例を用いて考えるにあたって<
<
の区間において、
と
軸に囲まれる領域の面積を求めるとします。
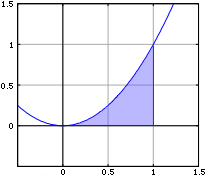
(高等学校数学III/積分法 - Wikibooks より)
ここで、計算は上記の定積分で表すことができます。これを計算すると下記のようになります。
このように、関数と軸で囲まれた領域の面積を求めることができます。
以下、下記の定積分について確認を行います。
1)
2)
3)
4)
5)
計算結果は下記のようになります。
1)
2)
3)
4)
5)
結果の解釈にあたっては、1)〜3)はと基本的に同様ですが、
の次数が大きい方が
<
<
の区間では面積が小さくなることも同時に抑えておくと良いと思います。また、1)は
であり、三角形の面積の公式と対応づけることも可能です。
4)は1)と同様に台形の面積の公式と対応づけることができますが、ここで注意しておくと良いのが5)の結果がとなることです。定積分は基本的に面積と対応しますが、関数の値が
軸よりも下にある場合は符号も考慮しなければならないことは抑えておきましょう。
定積分と符号に関しては続く2節で取り扱うので、1節はここまでとします。
2. 定積分と符号
2節では1節の計算例の5)で出てきたようなケースを題材に定積分と符号について確認します。定積分は関数と軸で囲まれている部分の面積を表しますが、関数の符号には注意が必要です。具体的には関数が負の値を取る区間の積分は絶対値が面積と一致する負の値となります。
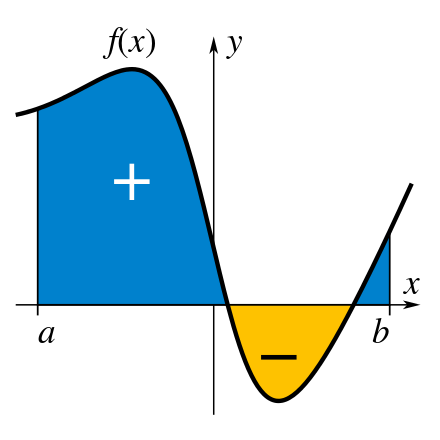
(積分法 - Wikipedia より)
上記はWikipediaの図ですが、こちらのイメージで掴むとわかりやすいです。