双曲線関数の概要を確認する（解析学基礎）｜式と曲線を把握する #4

f:id:lib-arts:20210618183529p:plain

数学Cなどで取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#1〜#3では「楕円」、「放物線」、「双曲線」の方程式とその導出について取り扱いました。

#4では#3の「双曲線」に関連して「双曲線関数」について取り扱います。主に下記を参考にします。

解析学基礎/双曲線関数 - Wikibooks

以下当記事の目次になります。
1. 双曲線関数とその概要について
2. 双曲線関数を用いた双曲線の描画
3. まとめ

1. 双曲線関数とその概要について
1節では「双曲線関数」とその概要について取り扱います。まずは双曲線関数の定義から確認します。

$\displaystyle \sinh{x} = \frac{e^x-e^{-x}}{2}$
$\displaystyle \cosh{x} = \frac{e^x+e^{-x}}{2}$

上記が双曲線関数の定義ですが、sinhはハイパーボリックサイン(hyperbolic sine)、coshはハイパーボリックコサイン(hyperbolic cosine)の略を意味します。

式の定義について確認できたので、次に双曲線関数の性質について確認します。

$\displaystyle \cosh^{2}{x} - \sinh^{2}{x} = 1$ ...①
$\displaystyle \sinh{(a+b)} = \sinh{a}\cosh{b}+\cosh{a}\sinh{b}$ ...②
$\displaystyle \cosh{(a+b)} = \cosh{a}\cosh{b}+\sinh{a}\sinh{b}$ ...③
$\displaystyle \frac{d}{dx}\sinh{x} = \cosh{x}$ ...④
$\displaystyle \frac{d}{dx}\cosh{x} = \sinh{x}$ ...⑤

上記はどれも三角関数に似た性質を持つので三角関数と同様の記号が用いられています。また、①の性質より、 $(x,y) = (\cosh{t},\sinh{t})$ のように双曲線関数を用いて双曲線上の点を表すことができます。これは通常の三角関数が $(x,y) = (\cos{t},\sin{t})$ のように単位円上の点を表すことができることと対応づけておくと良いです。

双曲線関数の式定義と簡単な性質について把握できたので1節はここまでとします。

2. 双曲線関数を用いた双曲線の描画
2節では双曲線関数を用いた双曲線の描画について取り扱います。1節でも簡単に取り扱いましたが、①の式が成立することの確認や具体的に双曲線を描画することで、双曲線関数について把握できればと思います。まずは①の式が成立することを確認します。

$\displaystyle \cosh^{2}{x} - \sinh^{2}{x} = \left( \frac{e^x+e^{-x}}{2} \right)^2 - \left( \frac{e^x-e^{-x}}{2} \right)^2$
　　 $\displaystyle = \frac{e^{2x}+2e^xe{-x}+e^{-2x}}{4} - \frac{e^{2x}-2e^xe{-x}+e^{-2x}}{4}$
　　 $\displaystyle = \frac{4e^xe{-x}}{4}$
　　 $\displaystyle = \frac{4}{4}$
　　 $= 1$

上記より①の式が成立することが確認できました。

次に、 $(x,y) = (\cosh{t},\sinh{t})$ のように双曲線関数を用いて双曲線の描画を行います。ここでは概要を掴むにあたって $=-2,-1,0,1,2$ の値を計算し、グラフを描画します。

・ $t=-2$
$\displaystyle (\cosh{-2},\sinh{-2}) = (\frac{e^{-2}+e^{2}}{2},\frac{e^{-2}-e^{2}}{2})$
　　 $= (3.762195691083631, -3.6268604078470186)$

・ $t=-1$
$\displaystyle (\cosh{-1},\sinh{-1}) = (\frac{e^{-1}+e^{1}}{2},\frac{e^{-1}-e^{1}}{2})$
　　 $= (1.5430806348152437, -1.1752011936438014)$

・ $t=0$
$\displaystyle (\cosh{0},\sinh{0}) = (\frac{e^{0}+e^{0}}{2},\frac{e^{0}-e^{0}}{2})$
　　 $= (1, 0)$

・ $t=1$
$\displaystyle (\cosh{1},\sinh{1}) = (\frac{e^{1}+e^{-1}}{2},\frac{e^{1}-e^{-1}}{2})$
　　 $= (1.5430806348152437, 1.1752011936438014)$

・ $t=2$
$\displaystyle (\cosh{2},\sinh{2}) = (\frac{e^{2}+e^{-2}}{2},\frac{e^{2}-e^{-2}}{2})$
　　 $= (3.762195691083631, 3.6268604078470186)$

計算結果から $(x,y)=(1,0)$ を通り、徐々に $x$ と $y$ の値が近づくことから双曲線が描けそうだということが確認できます。

また、以下ではPythonでの描画で確認してみます。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

t1 = np.arange(-2,2.1,0.1)
t2 = np.arange(-2,3,1)

plt.plot( (np.e**(t1)+np.e**(-t1) )/2., (np.e**(t1)-np.e**(-t1))/2., color="limegreen")
plt.scatter( (np.e**(t2)+np.e**(-t2) )/2., (np.e**(t2)-np.e**(-t2))/2.)

plt.show()

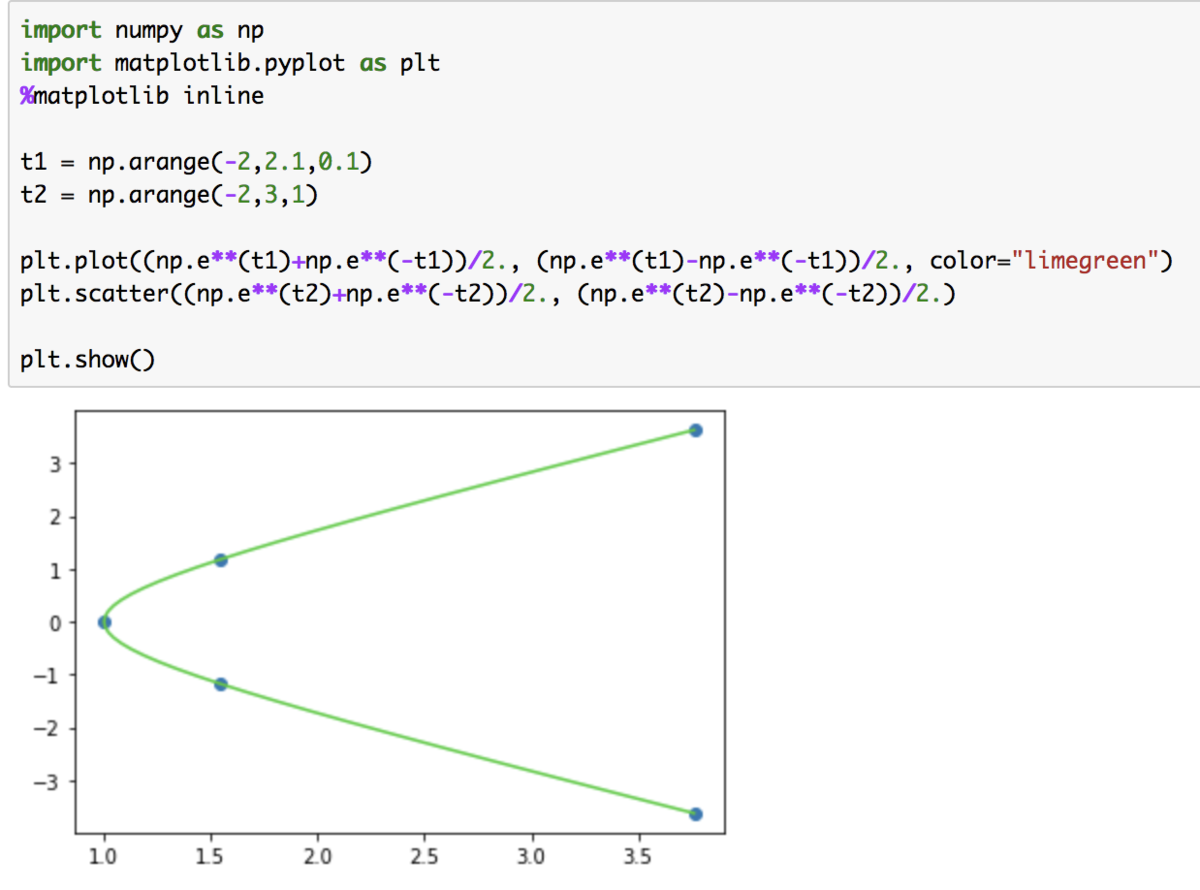
f:id:lib-arts:20210623171602p:plain