双曲線の方程式と導出｜式と曲線を把握する #3

f:id:lib-arts:20210618183529p:plain

数学Cなどで取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#1では「楕円」の方程式と導出、#2では「放物線」の方程式と導出について取り扱いました。

#3では「双曲線」の方程式と導出について取り扱います。主に下記を参考に進めます。

以下当記事の目次になります。
1. 双曲線の方程式とその概要
2. 双曲線の方程式の導出
3. まとめ

1. 双曲線の方程式とその概要
1節では「双曲線」の方程式とその概要に関して確認します。まずは双曲線の方程式について確認します。

$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ ①
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1$ ②
（ $a$ と $b$ は正の定数）

上記が双曲線の方程式です。概要を掴むにあたって①について考えます。具体的に考える方がわかりやすいので、 $y=0$ 、 $y=1$ 、 $y=2$ を考え、これに対応する $x$ の値を計算を行うとします。

・ $y=0$ のとき
$\displaystyle \frac{x^2}{a^2} = 1$
$x^2 = a^2$
$a$ ＞ $0$ より $x = \pm a$

・ $y=1$ のとき
$\displaystyle \frac{x^2}{a^2} - \frac{1}{b^2} = 1$
$\displaystyle \frac{x^2}{a^2} = 1+\frac{1}{b^2}$
$\displaystyle \frac{x^2}{a^2} = \frac{b^2+1}{b^2}$
$\displaystyle x^2 = \frac{a^2(b^2+1)}{b^2}$
$a$ ＞ $0$ より $x = \pm \frac{\sqrt{a^2(b^2+1)}}{b}$

・ $y=2$ のとき
$\displaystyle \frac{x^2}{a^2} - \frac{4}{b^2} = 1$
$\displaystyle \frac{x^2}{a^2} = 1+\frac{4}{b^2}$
$\displaystyle \frac{x^2}{a^2} = \frac{b^2+4}{b^2}$
$\displaystyle x^2 = \frac{a^2(b^2+4)}{b^2}$
$a$ ＞ $0$ より $x = \pm \frac{\sqrt{a^2(b^2+4)}}{b}$

$y$ に具体的な数値を入れて確認しましたが、これでもまだ具体的なイメージがつかめないので $a=b=1$ を代入して値を確認することとします。

・ $y=0$ のとき
$x = \pm 1$

・ $y=1$ のとき
$x = \pm \frac{\sqrt{a^2(b^2+1)}}{b}$
　　 $= \pm \frac{\sqrt{1^2(1^2+1)}}{1}$
　　 $= \pm \sqrt{2}$

・ $y=2$ のとき
$x = \pm \frac{\sqrt{a^2(b^2+4)}}{b}$
　　 $= \pm \frac{\sqrt{1^2(1^2+4)}}{1}$
　　 $= \pm \sqrt{5}$

これより、 $\displaystyle x = \sqrt{y^2+1}$ のようなイメージを持つと良いと思います。

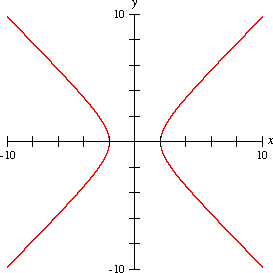
f:id:lib-arts:20210622163617p:plain

（双曲線 - Wikipedia より）
大まかな図は上記のようになります。また、双曲線には2つの漸近線が存在し、それぞれ $bx+ay=0$ 、 $bx-ay=0$ で表すことができます。

双曲線の数式とその概要について大まかに抑えられたので1節はここまでとします。

2. 双曲線の方程式の導出
2節では双曲線の方程式の導出について確認します。双曲線の定義は、「平面状にある2定点(焦点)からの距離の差が一定になるような点の集合からなる曲線」というものです。以下、2つの焦点を $(c,0)$ 、 $(-c,0)$ 、焦点からの距離の差を $2a$ とおき、双曲線の方程式を導出します。

まず、定義より下記が成立します。
$\displaystyle |\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}| = 2a$
$\displaystyle \sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2} = \pm 2a$
$\displaystyle \sqrt{(x-c)^2+y^2} = \sqrt{(x+c)^2+y^2} \pm 2a$
ここで上記の二乗を行います。
$\displaystyle (x-c)^2+y^2 = (x+c)^2+y^2 \pm 4a\sqrt{(x+c)^2+y^2} + 4a^2$
$\displaystyle ((x-c)^2+y^2)-((x+c)^2+y^2+4a^2) = \pm 4a\sqrt{(x+c)^2+y^2}$
$\displaystyle -4(a^2+cx) = \pm 4a\sqrt{(x+c)^2+y^2}$
$\displaystyle -(a^2+cx) = \pm a\sqrt{(x+c)^2+y^2}$
さらに上記の両辺を再度二乗します。
$\displaystyle (a^2+cx)^2 = a^2((x+c)^2+y^2)$
$\displaystyle a^4+2a^2cx+c^2x^2 = a^2(x^2+2cx+c^2+y^2)$
$\displaystyle a^4+2a^2cx+c^2x^2 = a^2x^2+2a^2cx+a^2c^2+a^2y^2$
$\displaystyle a^4+c^2x^2 = a^2x^2+a^2c^2+a^2y^2$
$\displaystyle (c^2-a^2)x^2-a^2y^2 = a^2c^2-a^4$
$\displaystyle (c^2-a^2)x^2-a^2y^2 = a^2(c^2-a^2)$
ここで $b^2=c^2-a^2$ と置き換えます。
$\displaystyle b^2x^2-a^2y^2 = a^2b^2$
さらにここで両辺を $a^2b^2$ で割ります。
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$
上記が楕円の方程式に一致します。