Pythonで実装する関数②（指数関数、対数関数）｜Pythonで実装する高校数学 #2

f:id:lib-arts:20190726175012p:plain

連載の経緯と多項式関数と三角関数の概要とPython実装は#1でまとめました。
https://lib-arts.hatenablog.com/entry/math_Python1
#2では同様に基本的な関数について取り扱うにあたって、指数関数と対数関数について取り扱います。
以下目次になります。
1. 指数関数の概要と実装
2. 対数関数の概要と実装
3. まとめ

1. 指数関数の概要と実装
1節では指数関数について取り扱います。指数関数は $2^x$ や $e^x$ など、ある数の $x$ 乗という形で関数を表現する関数です。
まずは#1と同様にWikipediaの記述を元に概要を把握します。

f:id:lib-arts:20190726212349p:plain
指数関数 - Wikipedia
指数関数(exponential function)は「指数(exponent)を変数として、その定義域を主に実数の全体へ拡張して定義される初等超越関数の一種」とされています。このように記述すると難しいですが、 $2^x$ や $e^x$ のようにxを用いる関数だと考えておくと良いです。指数関数の特徴としては、上記の右側のグラフにもあるように、 $x=0$ において1を取る、底が1より大きい際はx->-∞の際に0に限りなく近づく、また $x=1$ の時は底の値を取るということを把握しておくと良いです。また、底のaが0<a<1においてはグラフの形はy軸を中心にひっくり返したグラフとなります。

説明が長くなると難しくなるので、以下は実装を元に解説していきます。下記では様々な底aに対して、指数関数のグラフを記述しています。

import numpy as np
import math
import matplotlib.pyplot as plt

x = np.arange(-3,3.1,0.1)
y_2 = 2**x
y_3 = 3**x
y_e = math.e**x
y_0_5 = 0.5**x

plt.plot(x,y_2,label="a=2")
plt.plot(x,y_3,label="a=3")
plt.plot(x,y_e,label="a=e")
plt.plot(x,y_0_5,label="a=0.5")
plt.legend()
plt.show()

実行結果は下記のようになります。

f:id:lib-arts:20190726214147p:plain

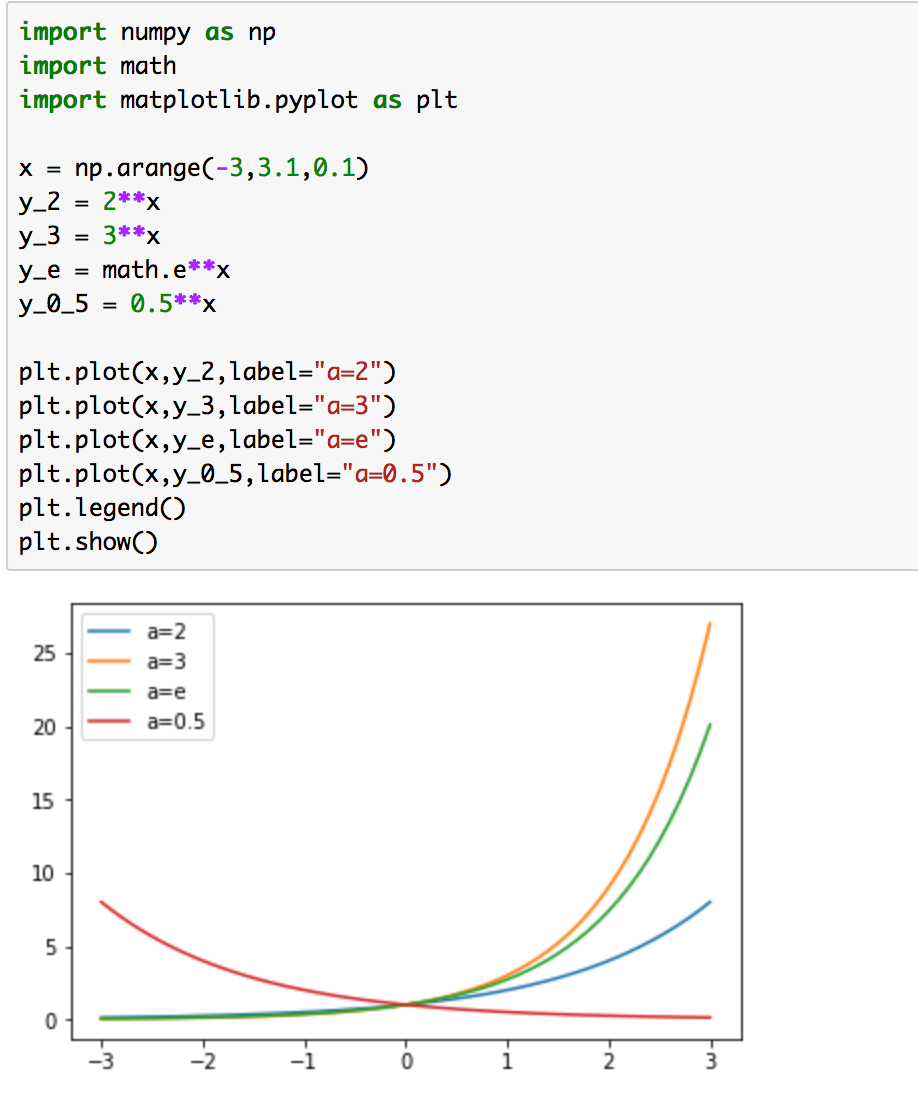
底aの値が1より大きい、2、3、e(2.718..)に関してはグラフは右肩上がりになっており、反対に1より小さい0.5に関してはグラフは右肩下がりになっていることが確認できます。また、全てのグラフが $x=0$ で交わっており、グラフが(0,1)を必ず通ることがこの図からも確認できます。
またここで急にeが出てきますが、eはネイピア数とも呼ばれており、大体2.718くらいの値になります。最初のうちはここで考え過ぎるよりは他のトピックを優先する方が良いので一旦は細かく意識はせずに、大体2.7くらいの数と捉えておくのが良いと思います。eについてはmathモジュールをインポートし、math.eで定数として値を取り出すことができます。

上記の内容で指数関数の概要とPython実装について一通り確認できたので、1節はここまでとします。

2. 対数関数の概要と実装
2節では対数関数について取り扱います。対数関数は変数xが底の何乗かを計算する関数で指数関数の逆関数になり、 $log_{2}(x)$ や $log_{10}(x)$ のように表記します。
まずはWikipediaの記述を元に概要を把握します。

f:id:lib-arts:20190726222910p:plain

対数 - Wikipedia

対数関数(logarithm function)は、 $log_{b}(x)$ のように表現します。この時のxを真数、bを底とし、xがbの何乗かを $log_{b}(x)$ は表しています。指数関数と同様に底bが0<b<1の範囲にあるか、1<bの範囲にあるかで大きく挙動が異なります。

f:id:lib-arts:20190726223556p:plain

1<bの際のグラフとしては上記のようになります。xの値が大きくなるにつれて例えば底を10と取れば、オーダー(桁)が変わるにつれて $log_{10}(x)$ は1ずつ大きくなっていきます。細かい数値に意味がなくても桁数だけは把握しておきたいケースが世の中にはあることから、こういったケースでは対数が用いられることが多いです。

大体の概要がつかめたので、以下では実装を確認していきます。

import numpy as np
import math
import matplotlib.pyplot as plt

x = np.arange(0.1,3.1,0.1)
y_log2 = np.log2(x)
y_log10 = np.log10(x)
y_loge = np.log(x)
y_log0_5 = -np.log2(x)

plt.plot(x,y_log2,label="b=2")
plt.plot(x,y_log10,label="b=10")
plt.plot(x,y_loge,label="b=e")
plt.plot(x,y_log0_5,label="b=0.5")
plt.legend()
plt.show()

上記の実行結果は下記のようになります。

f:id:lib-arts:20190726224700p:plain

まずbが2の時と0.5の時がx軸を中心に対称となっているのが読み取れます。これは2の1乗が0.5の-1乗と等しく、0.5の1乗が2の-1乗と等しいことなどと関連付けながら理解すると良いと思います。次にb=2とb=10ではb=10の方がなだらかなグラフになっています。こちらについては10進数の方が2進数よりも桁が変わるのが遅いということと同様な意味だと捉えるとわかりやすいです。

上記で大体の概要とPython実装について把握できたので2節はここまでとします。

3. まとめ
#2では指数関数と対数関数について取り扱いました。#1と#2で高校レベルの中心となる初等関数の大半を取り扱えたので、関数に関してはここまでとします。
#3以降では微分について話を進めていきます。