XAIの概要を把握する｜LIMEとSHAPの手法の確認 #2

f:id:lib-arts:20220409221345p:plain

当シリーズではXAIの研究の概要の把握を行います。#1ではSurveyを元に大まかな体系の確認を行いました。

#2では汎用的に用いることの可能なModel-Agnosticな手法であるLIMEやSHAPに関して、それぞれの論文を元に確認を行います。

[1602.04938] "Why Should I Trust You?": Explaining the Predictions of Any Classifier

[1705.07874] A Unified Approach to Interpreting Model Predictions

以下が目次となります。
1. LIMEの概要
2. SHAPの概要
3. まとめ

1. LIMEの概要

f:id:lib-arts:20220409221857p:plain

上記はLIMEの論文のSection3の冒頭部ですが、LIMEは"Local Interpretable Model-agnostic Explanations"の略であることが確認できます。"agnostic"は#1で取り扱いましたが、「ソフトウェアやハードウェアが特定のシステムに依存しないこと」を意味します。

また、ここでの"local"は「ある特定のサンプルの近傍(vicinity)」という意味であり、関数のテイラー展開と同様に理解すると良いと思います。

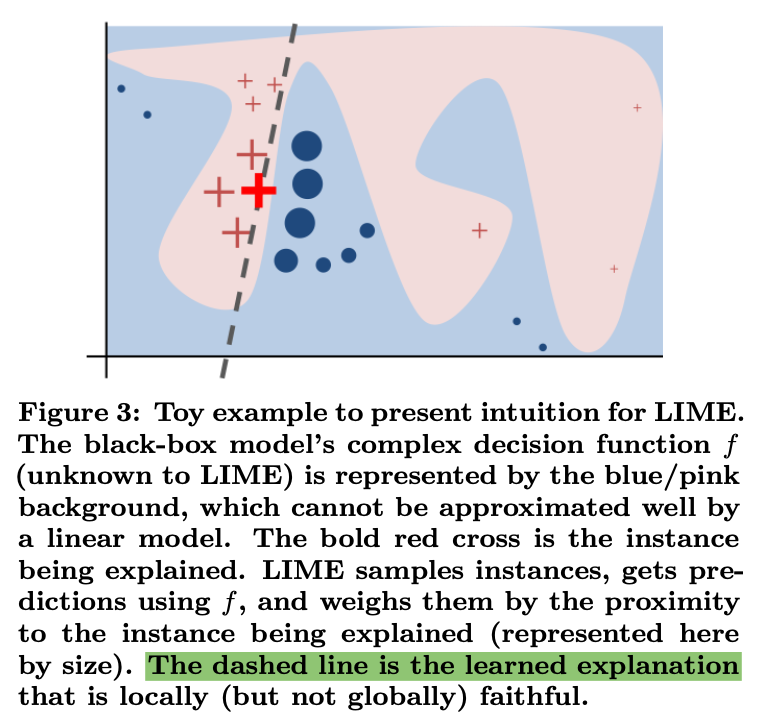
f:id:lib-arts:20220409223644p:plain

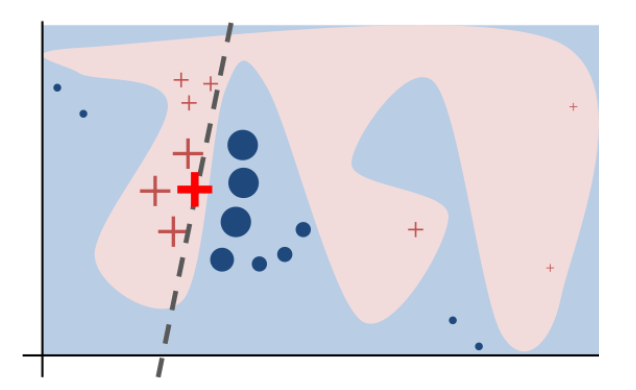
LIMEの概要に関しては上記のLIMEの論文のFigure.3を確認するとわかりやすいです。赤と青の領域が分類結果の際に、bold体の赤の×の近傍のサンプルの予測結果を元にグレーのdashed lineを学習し、これによって解釈を行います。

f:id:lib-arts:20220409224102p:plain

Figure.3のようなLIMEの学習結果の作成にあたっては、上記で定義されるlocality-aware lossの $\mathscr{L}(f,g,\pi_{x})$ と、 $g$ の複雑さ(complexity measures)を表す $\Omega(g)$ を用います。

ここで複雑な $f$ を、特定のサンプルの近傍の予測結果に基づき、linear modelのような単純な $g$ で近似を行うというのがLIMEの概要です。

f:id:lib-arts:20220409225052p:plain

また、特定のサンプルの近傍の値の生成は、上記のように乱数などを用いて近傍の入力を生成し、それを $f$ で予測した結果を元に $g$ の学習を考えます。この考え方は摂動(perturbations)と表されることも多いので抑えておくと良いと思います。

ここまでの内容を元に、LIMEの手順をまとめると下記のようになります。

① 摂動によって特定のサンプルの近傍の入力値を作成
② 解釈対象の $f$ を用いて入力値を予測
③ ①で生成した入力と②で生成した出力の組を元に、locality-aware lossの $\mathscr{L}(f,g,\pi_{x})$ とcomplexity measuresの $\Omega(g)$ を基準に $g$ で $f$ の近似を行う

f:id:lib-arts:20220409230120p:plain

また、locality-aware lossで用いられている $\pi_{x}$ は上記で示されるように、①で $x$ から摂動によって生成された $z$ の $x$ との類似度(proximity measure)を表すと理解すると良いです。

ここまでの内容でLIMEの手順について確認を行いましたが、LIMEの概要をまとめるなら「複雑な $f$ を特定のサンプル $x$ の近傍の $z$ の予測結果 $f(z)$ を元に、シンプルな関数 $g$ を学習し、 $g$ を元に $f$ の解釈を行う」と理解すると良いと思います。

2. SHAPの概要

f:id:lib-arts:20220409233204p:plain

上記がSHAPの論文のAbstractですが、SHAPは"SHapley Additive exPlanations"の略で、ゲーム理論におけるShapley Valueの知見を元に特徴量に関して加法的な(additive)説明を行うというのがSHAPの概要です。

additiveと表されると難しく見えますが、単にlinear model以外もlinear modelのように $\displaystyle y = b_0 + \sum_{i=1}^{n} b_i x_i$ の形式で統一的に取り扱えるようにShapley Valueの考え方を活用すると理解すれば良いです。

当記事ではまずSHAPの基盤の考え方であるShapley Valueに関して確認します。

f:id:lib-arts:20220409235047p:plain

Shapley Valueに関しては上記の論文 $(4)$ 式が理解できれば十分だと思います。式は複雑に見えますが、表記を1つ1つ確認すればそれほど難しくありません。まず、 $S, F$ に関しては $F$ が全ての特徴量の集合を表し、 $S$ はその部分集合(subsets)を表します。

また、 $f_{S \cup \{i\}}(x_{S \cup \{i\}}) - f_{S}(x_{S})$ は $S$ で表した特徴量に特徴量 $i$ を加えた際に予測値がどのように変化するかを表します。ここで部分集合 $S$ に特徴量 $i$ を加えることから、 $\displaystyle \sum$ の下では $i$ 以外の $F$ に含まれる部分集合 $S$ を用いるとされていることに注意が必要です。

さらに $|S|$ や $|F|$ はそれぞれの特徴量の要素の数を表すことから、 $\displaystyle \frac{|S|!(|F|-|S|-1)!}{|F|!} = \frac{1}{|F| \times {}_{|F|-1} C_{|S|}}$ は $S$ の選び方が多い $|S|$ に補正をかけると理解すれば良いです。