勾配ブースティング(Gradient Boosting)を理解する

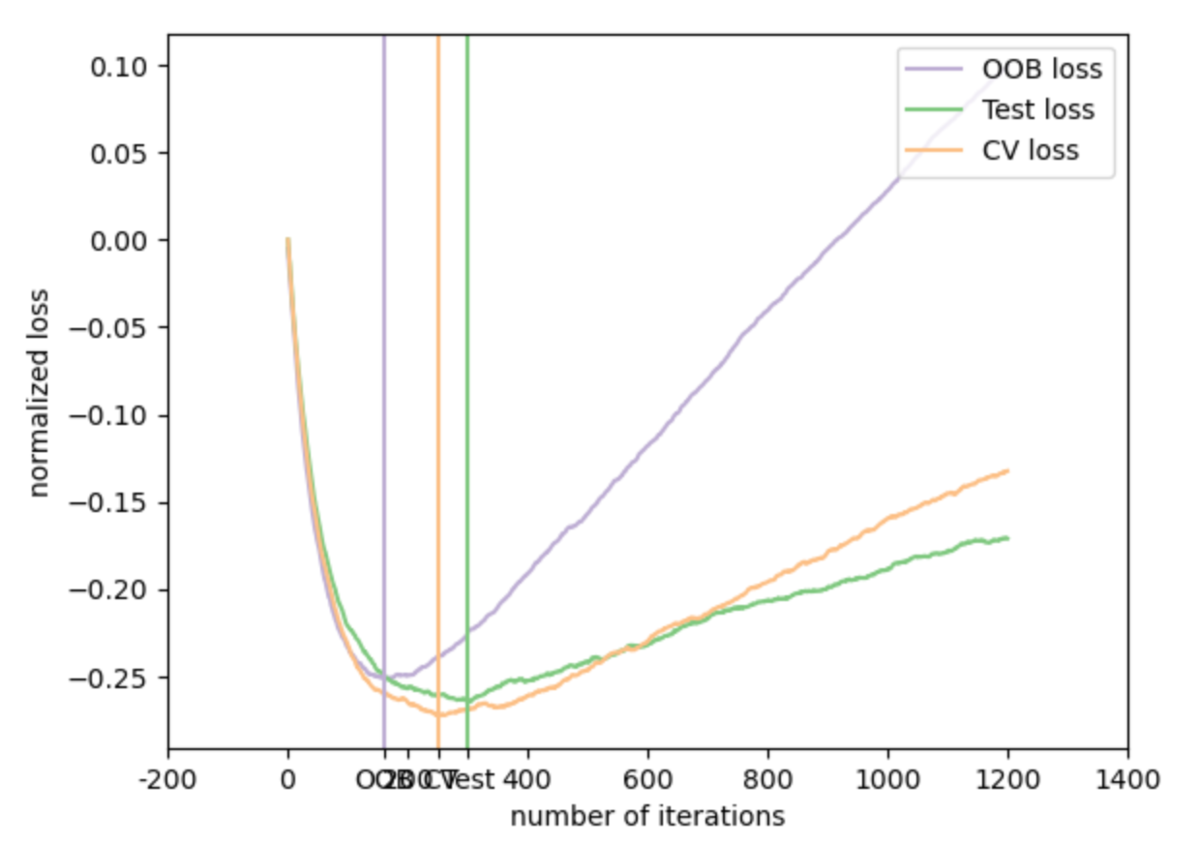
f:id:lib-arts:20210303222750p:plain

（↑from scikit-learn User Guide

Gradient Boosting Out-of-Bag estimates — scikit-learn 0.24.1 documentation）

当記事では勾配ブースティング(Gradient Boosting)について簡単に確認を行います。

勾配ブースティングについては少々フォーマルな記載が多く理解が大変なのですが、上記の「scikit-learnとTensorFlowによる実践機械学習」の記述が比較的わかりやすいので、こちらを元に簡単に確認したのちにWikipediaの記載を簡単に確認します。
以下、今回の目次になります。
1. 概要の把握
2. Wikipediaの確認
3. まとめ

1. 概要の把握
1節では「scikit-learnとTensorFlowによる実践機械学習」の記述を主に参考にしながら簡単な確認を行います。

O'Reilly Japan - scikit-learnとTensorFlowによる実践機械学習

まず、そもそもブースティングという考え方ですが、複数の学習器を用いて学習するアンサンブル学習の一種です。ブースティングの特徴としては、構成する学習器を一つずつ作成することで複数の学習器を総括した全体のパフォーマンスを高めようというものです。ブースティングの例としては、当記事で取り扱う勾配ブースティング以外であれば、局所特徴量ベースの画像処理の学習で用いられたAdaBoostなどが例としてはあります。

さて、今回のテーマの勾配ブースティングですが、細かい内容よりもイメージから入るのが良いかと思います。勾配ブースティングのイメージとしてはフーリエ展開に発想としては近く、学習器を一つずつ学習させていくにあたって、それまでの分類器と正解の値の差を以降の学習器で学習を行うというものです。

説明だけだとわかりにくいので数式的に確認すると、1つ目の学習器の $i$ 番目のサンプルの予測結果(予測目標)を $\hat{y}_i^{(1)}$ 、 $i$ 番目のサンプルの結果を $y_i$ とすると、2つ目の学習器の予測目標は $y_i-\hat{y}_i^{(1)}$ となります。また、ここでこの2つ目の学習器の予測値を $\hat{y}_i^{(2)}$ とすると、3つ目の学習器の予測目標は $y_i-(\hat{y}_i^{(1)}+\hat{y}_i^{(2)})$ となります。

このように学習器を学習させ、最終的には予測結果を $\hat{y}_i^{(1)}+\hat{y}_i^{(2)}+...+\hat{y}_i^{(n)}$ のように表すのが勾配ブースティングの主な流れです。

2. Wikipediaの確認
2節では勾配ブースティングのWikipediaの記載を確認します。（記載の内容がいまいち掴めなかったため独自で式を再定義し改変し、参照元とは異なる内容となりましたことにご留意ください。）

Gradient boosting - Wikipedia

f:id:lib-arts:20210303211700p:plain

上記で1節と同様の内容がもう少しフォーマルな形式で記述されていますが、少々違和感がありますので、以下は独自解釈で数式を再定義しつつまとめます。

ブースティングの各段階における学習器の予測目標(残差; residual とも考えられる)を $h_{m}(x)$ 、各段階において学習させた学習器の予測結果を $\hat{y}_i^{(m)}$ 、学習器全体の予測結果を $F_m(x)=\hat{y}_i^{(1)}+\hat{y}_i^{(2)}+...+\hat{y}_i^{(m)}$ で表した際に、全体の誤差関数を $\displaystyle L_{MSE}=\frac{1}{2}(y-F_m(x))^2$ で表すとすると、誤差関数 $L_{MSE}$ の $F_m$ に関する勾配にマイナスをかけた値として、残差の $h_{m+1}(x)$ が計算できます。この時 $1 \leqq m$ と $m+1 \leqq n$ が満たされるとした上で、全体で $n$ 回のブースティングを行うとします。

Wikipediaの記載では $F(x)$ が明示的でないので、より明示的に表すとすると、

$\displaystyle h_{m+1}(x)=-\frac{\delta L_{MSE}}{\delta F_m}=y-F_m(x)$

のように表すことができるかと思います。 $h_{m}(x)$ をフィッティング(学習)して予測した結果が $\hat{y}_i^{(m)}$ なので、最終的には予測結果を $F_{n}=\hat{y}_i^{(1)}+\hat{y}_i^{(2)}+...+\hat{y}_i^{(n)}$ のように表すことができます。

また、この際に $\hat{y}_i^{(m)}$ を $L_{MSE}$ の最小化にあたっての繰り返し計算における更新分のように見なすことで、勾配降下法(Gradient Descent)に特殊化できると考えることができます。 $\displaystyle F_{m+1}=F_m-(\frac{\delta L_{MSE}}{\delta F_m})=F_m+\hat{y}_i^{(m)}$ のように $F_m$ の更新を行っていくイメージです。

また、この際に $\displaystyle F_{m+1}=F_m-(\alpha \frac{\delta L_{MSE}}{\delta F_m})=F_m+\alpha \hat{y}_i^{(m)}$ として $\alpha=0.1$ などのように1より小さい値を設定することでブースティングの回数の $n$ の数を増やす必要性がある一方で頑健性を高めるという考え方もあるようです。この場合は $F_m(x)=\alpha(\hat{y}_i^{(1)}+\hat{y}_i^{(2)}+...+\hat{y}_i^{(m)})$ のように学習器全体を計算することが可能です。