XAIの概要を把握する|DeepLearningの解釈の3分類の案に関して #5
当シリーズではXAIの研究の概要の把握を行います。#4ではDeepLIFTとGrad-CAMに関して確認を行いました。
#5では#3の4節で取り扱った"Explaining Explanations: An Overview of Interpretability of Machine Learning"を元に、DeepLearningの解釈にあたっての3分類に関して確認を行います。
[1806.00069] Explaining Explanations: An Overview of Interpretability of Machine Learning
以下が目次となります。
1. 分類の概要
1-1. Processing
1-2. Representation
1-3. Explanation Producing
2. まとめ
1. 3分類の概要
3分類の概要に関しては論文のSectionVのTaxonomyで取り扱われています。
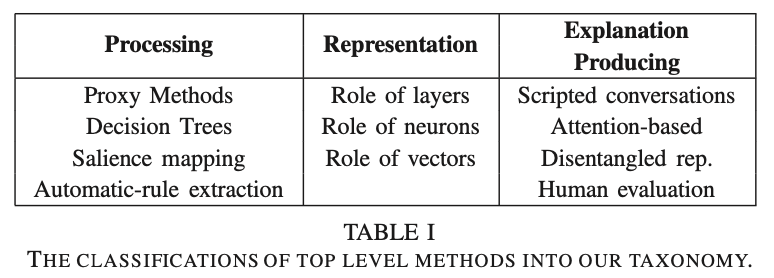
上記で表した論文のTable.1で3つの分類に関してまとめられています。
Processing、Representation、Explanation Producingの3つが挙げられています。それぞれについて詳しくはSectionⅢのReviewで取り扱われているので以下、確認を行います。
また、ProcessingではDecision Treeなどが出てきますが、Processingに関してはLIMEのようなsimplificationの意味合いで取り扱われているので、あくまでDeepLearningの分類で用いられていると考えて良いようです。
1-1. Processing
1-1節ではSectionⅢのAの"Explanations of Deep Network Processing"を元にProcessingの詳細に関して確認を行います。

上記が冒頭部の記載ですが、simplificationの実現にあたって、"proxy model"や"salience map"を作成することについて言及されています。"proxy model"は"Linear Proxy Models"や"Decision Trees"らが対応し、"salience map"は"Salience Mapping"に対応してそれぞれ後述されると考えて良いようです。

(中略)

上記のように"Linear Proxy Models"や"Decision Trees"ではそれぞれ"proxy model"と記載があります。"proxy"は代理などの意味合いの単語ですが、LIMEのようにシンプルに近似を行うことをここでは"proxy"と表現していると理解すれば良いと思います。
1-2. Representation
1-2節ではSectionⅢのBの"Explanations of Deep Network Representations"を元にRepresentationの詳細に関して確認を行います。
Role of Layers、Role of Individual Units、Role of Representation Vectorsのそれぞれ三つが紹介されています。
1-3. Explanation Producing

上記のようにTransformerなどで用いられる考え方のAttentionなどが紹介されています。
2. まとめ
#5では"Explaining Explanations: An Overview of Interpretability of Machine Learning"を元に、DeepLearningの分類に関して取り扱いました。
#6では#4で取り扱ったDeepLIFTでも言及された、LRP(Layerwise Relevance Propagation)に関して取り扱いを行います。
XAIの概要を把握する|DeepLIFT、Grad-CAMの概要の把握 #4

当シリーズではXAIの研究の概要の把握を行います。#3ではDeepLearningに関する解釈に関して取り扱いを行いました。
#4では#3で出てきたDeepLIFTやGrad-CAMに関して論文の内容の確認を行います。
[1704.02685] Learning Important Features Through Propagating Activation Differences
[1610.02391] Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization
以下が目次となります。
1. DeepLIFTに関して
2. Grad-CAMに関して
3. まとめ
1. DeepLIFTに関して
1節ではDeepLIFTの論文に関して確認を行います。

上記がAbstractの冒頭ですが、DeepLIFTは"Deep Learning Important FeaTures"の略で、「誤差逆伝播(backpropagation)を用いて予測結果に対する効果を入力の全ての特徴量に対して計算を行う」手法です。
Section2の"Previous work"では「特徴量重要度」を計算するいくつかの方法についてまとめられており、具体的には「① Perturbation-Based Forward Propagation Approaches」、「② Backpropagation-Based Approaches」、「③ Grad-CAM and Guided CAM」の三つが挙げられています。

上記はSection2.2の冒頭ですが、ここでDeepLIFTが「② Backpropagation-Based Approaches」の一手法であることについて記載があります。


DeepLIFTの詳細に関してはSection3の"The DeepLIFT Method"で記載されており、冒頭部では数式を用いた定義に関してまとめられています。DeepLIFTでは「解釈対象」と「ベースの入力のreference」の差分を考えることで、それぞれの特徴量の効果について計算を行います。target output neuronと表記される解釈対象のに関して差分を
のように表し、これを(1)式に基づいて考えられるように
を計算するというのがDeepLIFTの概要になります。
2. Grad-CAMに関して
2節ではGrad-CAMの論文に関して確認を行います。

上記がAbstractの冒頭ですが、Grad-CAM(Gradient-weighted Class Activation Mapping)は、誤差関数の勾配を用いて目的変数の予測に寄与した入力のハイライトを行う手法です。また、従来の手法とは違いGrad-CAMは広範なCNNのアーキテクチャに適用できると記載がされています。

Grad-CAMが広範に用いれることに関しては、上記のRelated Workで表されるCAM(Class Activation Mapping)ではアーキテクチャありきでヒートマップが作成されることと対比しながら抑えておくと良いと思います。
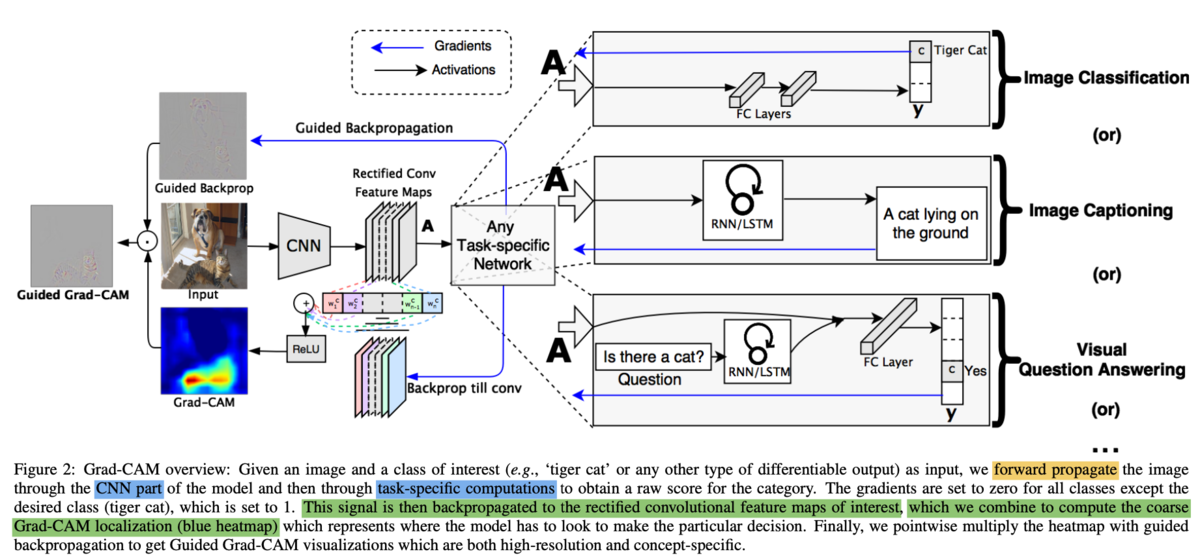
Grad-CAMの全体像は上記で表した論文のFigure.2で図示されており、誤差関数の勾配の誤差逆伝播を元にfeature map(畳み込みやPoolingを行った後のCNNの出力結果)に反映させ、feature mapを組み合わせることで青で表されたGrad-CAMのヒートマップを得ることができます。
![]()
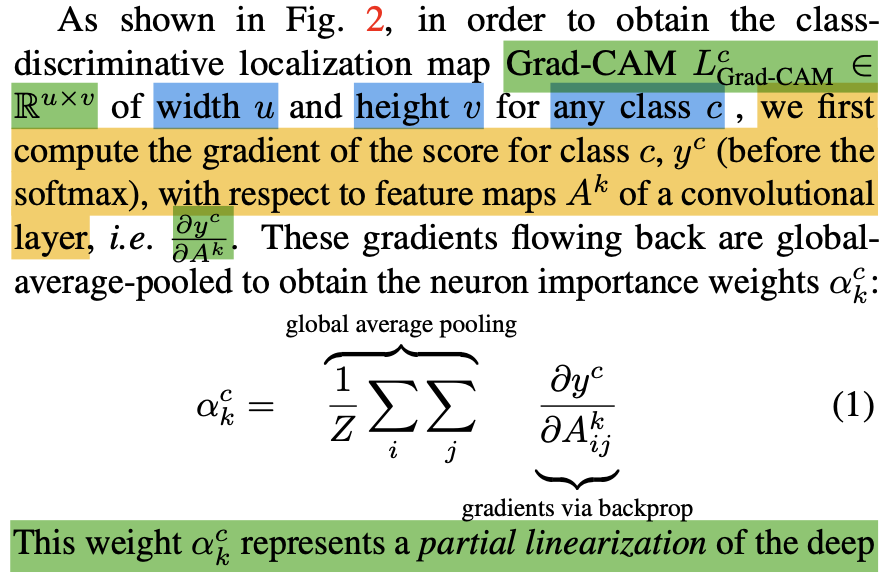
処理の詳細は上記のようにSection3でも記載されており、出力層のに対し、feature mapが
で表され、予測結果
に対する
番目のfeature mapの重要度が
で表されます。
このように計算したを用いてfeature mapの重み付け和を計算することで、ヒートマップを得ることができます。
3. まとめ
#4ではDeepLIFTやGrad-CAMに関して確認を行いました。
#5では#3の4節で取り扱った"Explaining Explanations: An Overview of Interpretability of Machine Learning"の確認を行います。
[1806.00069] Explaining Explanations: An Overview of Interpretability of Machine Learning
XAIの概要を把握する|DeepLearningに関するXAIの手法 #3
当シリーズではXAIの研究の概要の把握を行います。#2ではLIMEとSHAPに関して確認を行いました。
#3では#1で確認を行なったSurveyを元に、DeepLearningに関するModel-Specificな解釈に関して取り扱いを行います。
以下が目次となります。
1. Multi-Layer Neural Networks
2. Convolutional Neural Networks
3. Recurrent Neural Networks
4. 体系的な理解
5. まとめ
1. Multi-Layer Neural Networks
1節ではSurveyのSection4.3.1を元に、Multi-Layer Neural Networksに関して取り扱いを行います。

第1パラグラフの記載を確認することで、Multi-Layer Neural NetworksはMulti-Layer Perceptronと同じ意味で用いられていることが確認できます。
また、第2パラグラフではmodel simplificationに関する手法のDeepRedが挙げられており、続く第3パラグラフではInterpretable Mimic Learningが挙げられています。
その他にもDeepLIFTなどがmodel simplificationの例に紹介されています。
2. Convolutional Neural Networks
2節ではSection4.3.2の内容を元にCNNに関して確認を行います。

第2パラグラフを確認すると、CNNの理解に関する研究は「① 出力結果を判別するにあたって用いられた部分を確認するにあたって、入力空間にヒートマップを描き、意思決定過程を理解する」研究と、「② ニューラルネットワーク内部の挙動を掘り下げる(delve)」研究の二つに大別されるという記載があります。①の研究の具体的な例にGrad-CAM(Visual explanations from deep networks via gradient-based localization)があることは抑えておくと良いと思います。

Grad-CAMの概要は上記で表したFigure.7などで示されているので、こちらで大体の概要が掴めると思います。
②の研究に関しては、Deep Generator Network(DGN)などが例に挙げられています。
3. Recurrent Neural Networks
3節ではSection4.3.3の内容を元にRNNに関して確認を行います。

第2パラグラフを確認することで、model-agnosticで取り扱われた「①単純化(simplification)に基づく手法」と「②特徴量の関連に基づく手法」のような汎用的な考え方に概ね基づき、RNNの解釈に関する論文が大別されることが確認できます。
4. 体系的な理解
4節ではSurveyのSection4.4の内容の確認を行います。
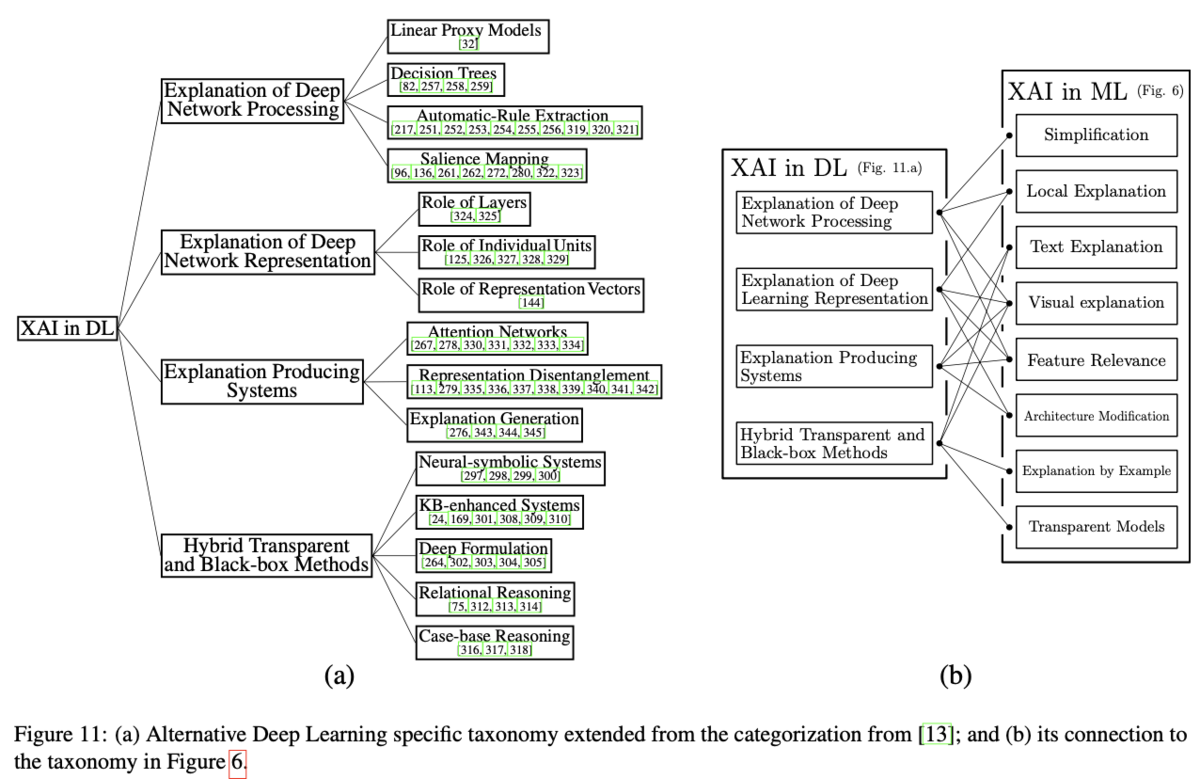
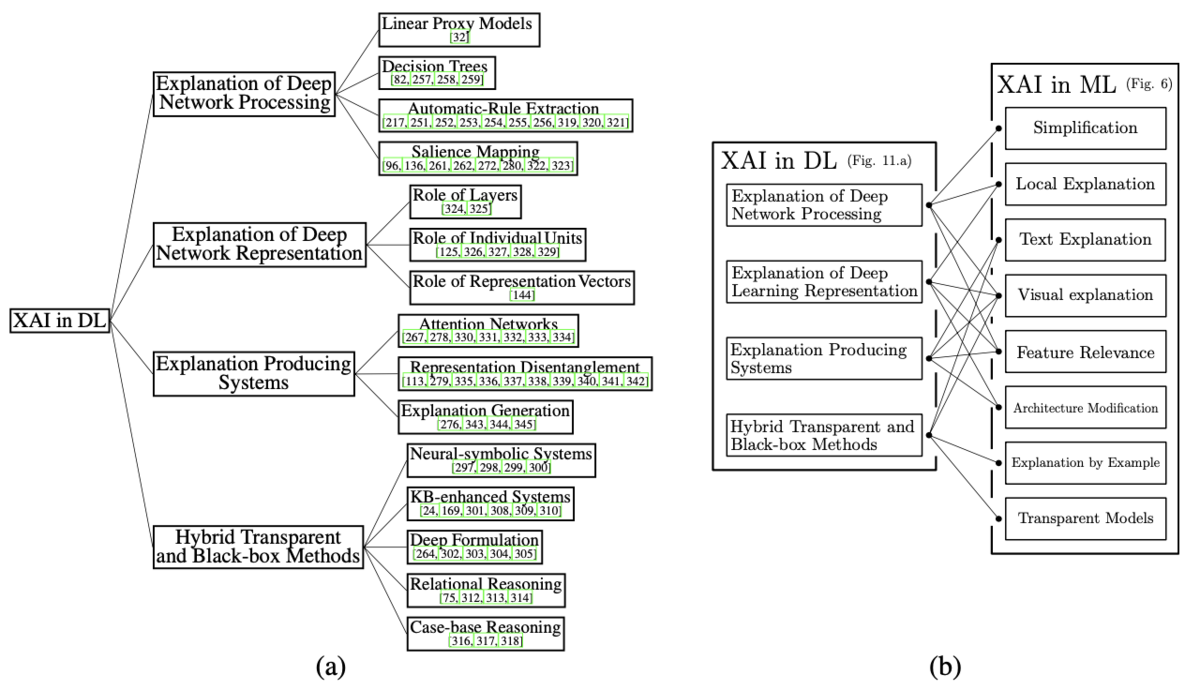
上記で示したFigure.11では、"Explaining Explanations: An Overview of Interpretability of Machine Learning"の内容を元に、DeepLearningの体系(taxonomy)が提示されます。
[1806.00069] Explaining Explanations: An Overview of Interpretability of Machine Learning
Surveyの記載だけで読み解くのは少々難しそうなので、詳細の確認は必要に応じて別途行おうと思います。
5. まとめ
#3ではXAIのSurveyからDeepLearningに関連する記載の確認を行いました。
#4では2節で確認を行なったDeepLIFT(Deep Learning Important Features)と、3節で確認を行なったGrad-CAMの論文の内容の確認を行います。
XAIの概要を把握する|LIMEとSHAPの手法の確認 #2
当シリーズではXAIの研究の概要の把握を行います。#1ではSurveyを元に大まかな体系の確認を行いました。
#2では汎用的に用いることの可能なModel-Agnosticな手法であるLIMEやSHAPに関して、それぞれの論文を元に確認を行います。
[1602.04938] "Why Should I Trust You?": Explaining the Predictions of Any Classifier
[1705.07874] A Unified Approach to Interpreting Model Predictions
以下が目次となります。
1. LIMEの概要
2. SHAPの概要
3. まとめ
1. LIMEの概要

上記はLIMEの論文のSection3の冒頭部ですが、LIMEは"Local Interpretable Model-agnostic Explanations"の略であることが確認できます。"agnostic"は#1で取り扱いましたが、「ソフトウェアやハードウェアが特定のシステムに依存しないこと」を意味します。
また、ここでの"local"は「ある特定のサンプルの近傍(vicinity)」という意味であり、関数のテイラー展開と同様に理解すると良いと思います。
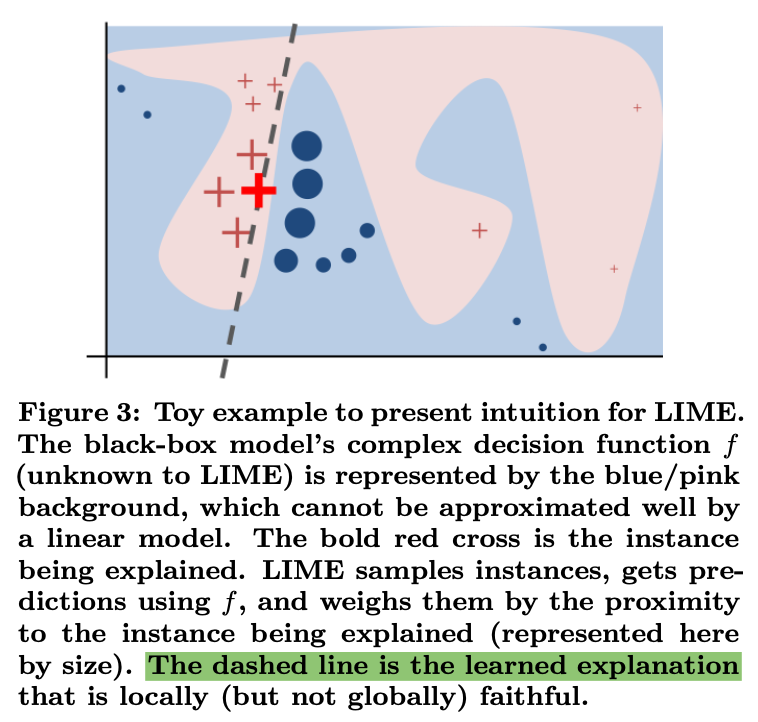
LIMEの概要に関しては上記のLIMEの論文のFigure.3を確認するとわかりやすいです。赤と青の領域が分類結果の際に、bold体の赤の×の近傍のサンプルの予測結果を元にグレーのdashed lineを学習し、これによって解釈を行います。

Figure.3のようなLIMEの学習結果の作成にあたっては、上記で定義されるlocality-aware lossのと、
の複雑さ(complexity measures)を表す
を用います。
ここで複雑なを、特定のサンプルの近傍の予測結果に基づき、linear modelのような単純な
で近似を行うというのがLIMEの概要です。

また、特定のサンプルの近傍の値の生成は、上記のように乱数などを用いて近傍の入力を生成し、それをで予測した結果を元に
の学習を考えます。この考え方は摂動(perturbations)と表されることも多いので抑えておくと良いと思います。
ここまでの内容を元に、LIMEの手順をまとめると下記のようになります。
① 摂動によって特定のサンプルの近傍の入力値を作成
② 解釈対象のを用いて入力値を予測
③ ①で生成した入力と②で生成した出力の組を元に、locality-aware lossのとcomplexity measuresの
を基準に
で
の近似を行う

また、locality-aware lossで用いられているは上記で示されるように、①で
から摂動によって生成された
の
との類似度(proximity measure)を表すと理解すると良いです。
ここまでの内容でLIMEの手順について確認を行いましたが、LIMEの概要をまとめるなら「複雑なを特定のサンプル
の近傍の
の予測結果
を元に、シンプルな関数
を学習し、
を元に
の解釈を行う」と理解すると良いと思います。
2. SHAPの概要

上記がSHAPの論文のAbstractですが、SHAPは"SHapley Additive exPlanations"の略で、ゲーム理論におけるShapley Valueの知見を元に特徴量に関して加法的な(additive)説明を行うというのがSHAPの概要です。
additiveと表されると難しく見えますが、単にlinear model以外もlinear modelのようにの形式で統一的に取り扱えるようにShapley Valueの考え方を活用すると理解すれば良いです。
当記事ではまずSHAPの基盤の考え方であるShapley Valueに関して確認します。

Shapley Valueに関しては上記の論文式が理解できれば十分だと思います。式は複雑に見えますが、表記を1つ1つ確認すればそれほど難しくありません。まず、
に関しては
が全ての特徴量の集合を表し、
はその部分集合(subsets)を表します。
また、は
で表した特徴量に特徴量
を加えた際に予測値がどのように変化するかを表します。ここで部分集合
に特徴量
を加えることから、
の下では
以外の
に含まれる部分集合
を用いるとされていることに注意が必要です。
さらにや
はそれぞれの特徴量の要素の数を表すことから、
は
の選び方が多い
に補正をかけると理解すれば良いです。
このように特徴量の効果の
を
式のような重み付け和によって計算することで、それぞれの特徴量の効果の計算を行います。

それぞれの計算の結果は上記のFigure.1のように図示されます。このように考えることでlinear model以外の手法を用いていてもlinear modelのような解釈を行うことができ、大変有用です。
3. まとめ
#2ではLIMEとSHAPに関して取り扱いを行いました。
#3ではDeepLearningに関するXAIの手法に関して取り扱いを行います。
XAIの概要を把握する|Surveyの構成と大枠の把握 #1

近年DeepLearningやその他複雑な機械学習の学習結果に対して説明を行う研究が行われており、XAI(eXplainable AI)などと総称されることが多いです。当記事では"SurveyのExplainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI"の内容を確認することで、体系的理解を目標に全体像の確認を行います。
以下が目次となります。
1. Surveyの構成の確認
2. XAIはどのように体系化すべきか
3. まとめ
1. Surveyの構成の確認
1節では参照するSurveyの構成の確認を行います。
Abstract
1 Introduction
2 Explanability: What, Why, What For and How?
3 Transparent Machine Learning Models
4 Post-hoc Explainability Techniques for Machile Learning Models: Taxonomy, Shallow Models and Deep Learning
5 XAI: Opportunities, Challenges and Future Research Needs
6 Toward Responsible AI: Principles of Artificial Intelligence, Fairness, Privacy and Data Fusion
上記が大まかな章立てです。
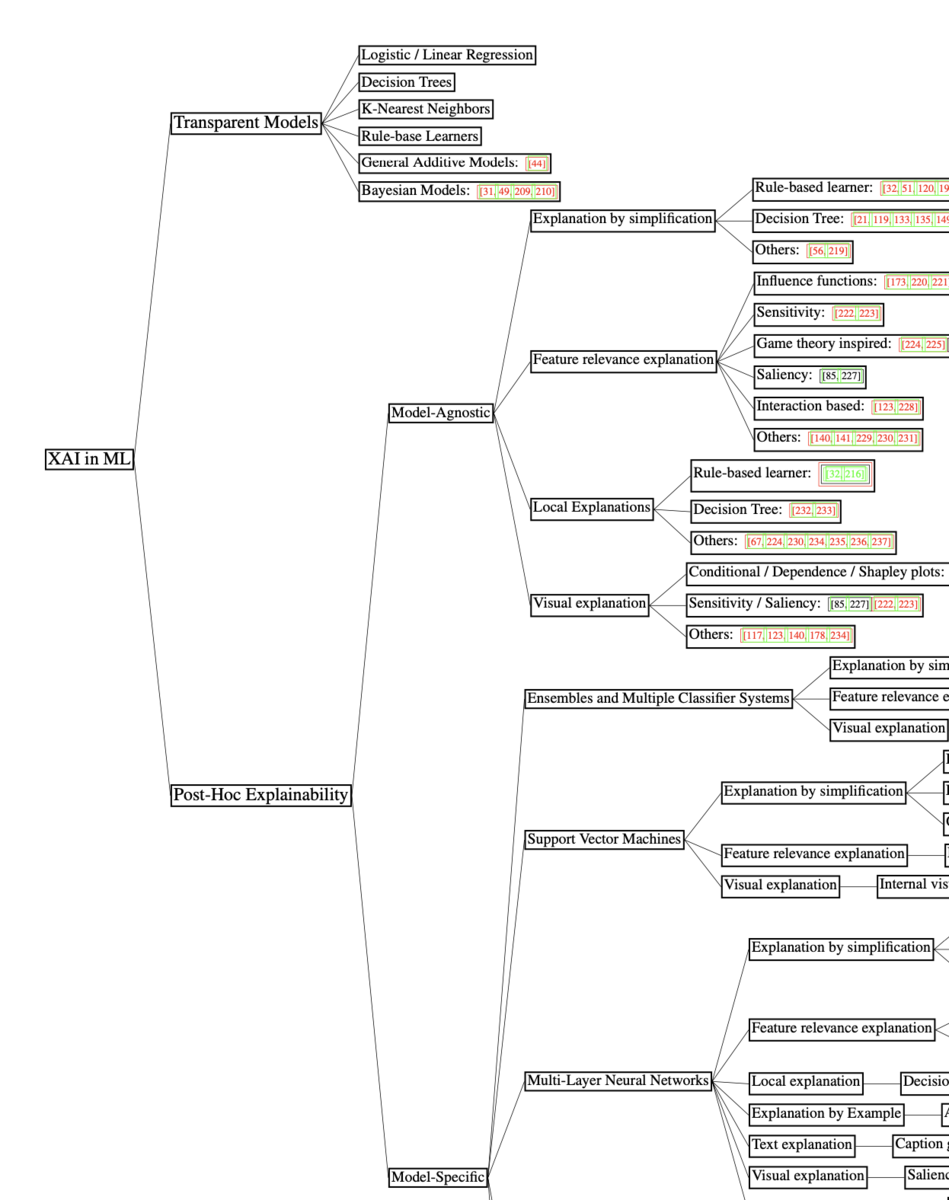
体系的理解にあたっては、上記のFigure.6が参考になります。"Transparent Models"がSection3に、Post-Hoc ExplanabilityがSection4にそれぞれ大まかに対応します。
それぞれの用語の意味は、Transparentが線形回帰(Linear Regression)や決定木(Decision Tree)などのように解釈が容易であることを指しており、Post-Hocは事後的に解釈をつけることを指すとざっくりと理解しておけば良いと思います。
Post-Hocの関連語に「その場の、暫定的な」の意味のAd-Hocがありますが、ざっくりとは「バッチ処理のように後からまとめて処理を行う」と「観測値を順々に処理を行う」の対比で、抑えておけば良いと思います。
大まかな体系的理解が当記事での目標なので、続く2節ではSurveyのSection3とSection4を元にXAIの体系化に関する確認や考察を行います。
2. XAIはどのように体系化すべきか

1節では上記で表したSurveyのFigure.6に基づいてSurveyの構成の確認を行いましたが、2節では体系化について詳しく確認や考察を行います。
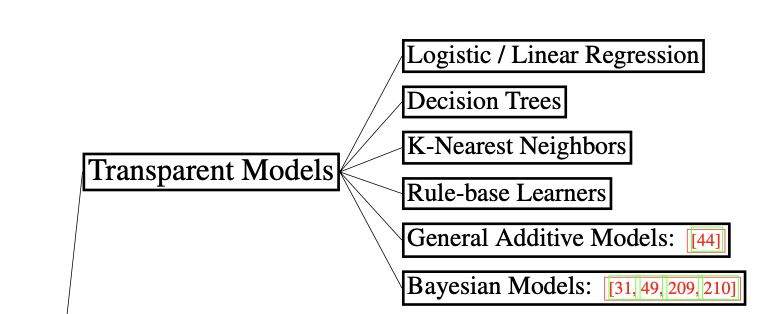
Section3でまとめられるTransparent Modelsは上記であり、どれも基本的な機械学習のアルゴリズムであることが確認できます。
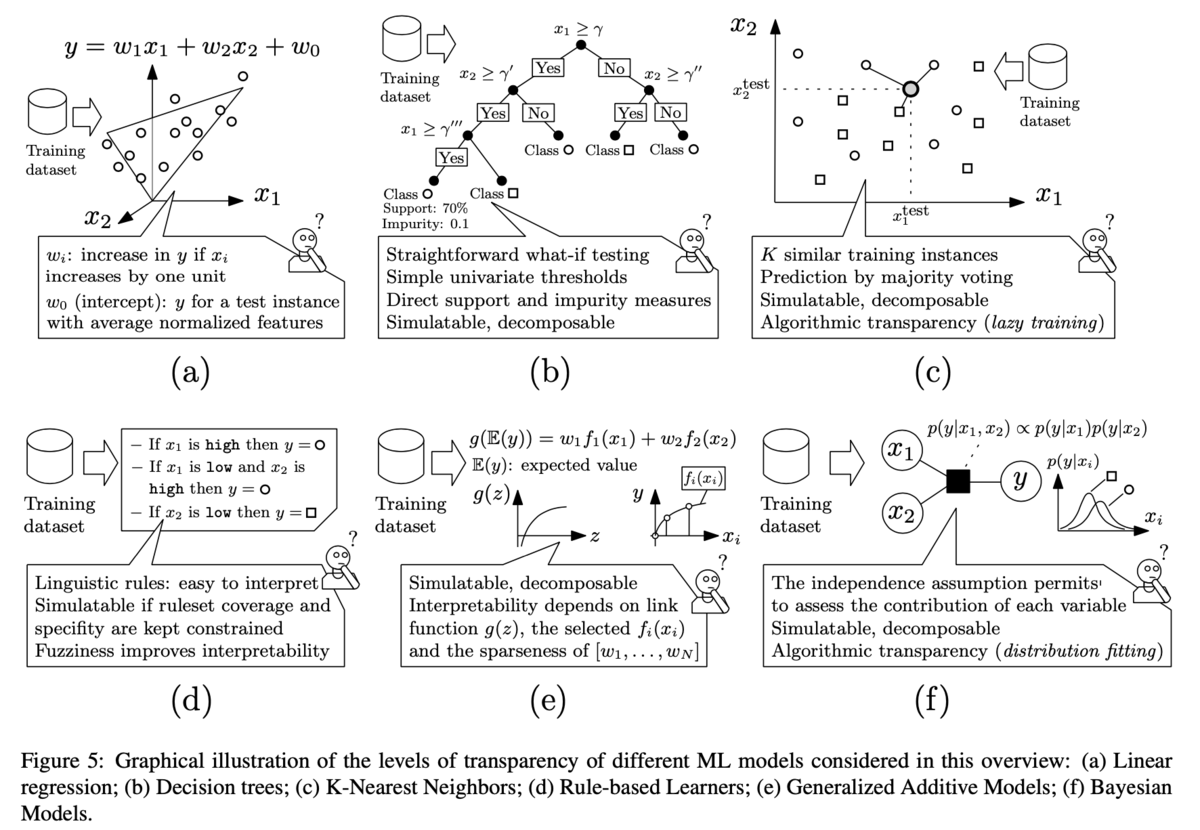
それぞれの手法に関してはFigure.5でまとめられており、上記を元に大まかに概要を掴むことができると思います。詳細の理解が必要であれば、PRML(Bishop本)などが詳しいのでそちらなどを参照すると良いと思います。
Section4でまとめられるPost-Hocな手法に関しては、手法に関係なく用いることができる"Model-Agnostic"の手法と、特定の手法に対応した"Model-Specific"の手法の二つに大別され、"Model-Agnostic"がSection4-1で、"Model-Specific"がSection4-2とSection4-3でそれぞれ解説されます。Section4-2ではアンサンブル学習やサポートベクトルマシンなどのShallowな手法が、Section4-3ではDeepLearningに関連してMLP、CNN、RNNなどが取り扱われます。
また、Section4-1の"Model-Agnostic"な手法では、「①単純化(simplification)に基づく手法」と「②特徴量の関連に基づく手法」が主に二つ挙げられており、①がLIMEに、②がSHAPにそれぞれ対応します。
3. まとめ
#1では"SurveyのExplainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI"の内容を元にXAIの体系的な整理を行いました。
続く#2では"Model-Agnostic"のところで出てきたLIMEとSHAPに関してそれぞれ論文を元に確認を行います。
Dynamic Headの論文の内容について |物体検出(Object Detection)の研究トレンドを俯瞰する #6
#1〜#5にかけてR-CNN、Faster R-CNN、FPN、RetinaNet、Cascade R-CNNなどについて取り扱いました。
〜
#6ではDynamic Head[2021]の論文について取り扱います。
[2106.08322] Dynamic Head: Unifying Object Detection Heads with Attentions
以下目次になります。
1. 論文の概要の把握(Abstract、Introductionの確認)
1-1 Abstractの確認
1-2 Introductionの確認(Section1)
2. 論文の重要なポイントの抜粋
2-1 Related Work(Section2)
2-2 Our Approach(Section3)
2-3 Experiment(Section4)
3. まとめ
1. 論文の概要の把握(Abstract、Introductionの確認)
1-1 Abstractの確認
1-1節ではAbstractの内容を簡単に確認します。

上記の要旨をまとめると以下になります。
・これまでの物体検出(Object Detection)の研究は様々な手法が開発され、パフォーマンスの向上が試みられてきたが、統合的な見方(unified view)の確立までには至らなかった。
・Dynamic headの論文ではAttentionの考え方に基づいてhead(backbone処理後のfeature mapを元にタスクを解く処理を行う部分)の統合的なフレームワークを示した。
・scale-awareness、spatial-awareness、task-awarenessに基づく複数のself-attentionのメカニズムを組み合わせることで、計算コストにオーバーヘッドを生じさせずにheadの表現力を著しく向上させた。
・記載の設定に基づいてCOCOベンチマークに置いてSotAを実現した。
・作成したcodeが公開された。
Abstractの大まかな要旨を確認できたので1-1節はここまでとします。
1-2 Introductionの確認(Section1)
1-2節ではIntroductionの内容を確認します。重要だと思われるパラグラフを抜粋し、確認を行います。

第一パラグラフでは、物体検出(Object Detection)タスクの概要や主要研究の紹介が行われています。参照論文の11がFast R-CNN、23がFaster R-CNNであることは抑えておくと良いと思います。また、最後の文で「object detection headのパフォーマンスの向上をどのように行うかが重要な課題とされてきた」と言及されており、この論文の問題提起が行われています。


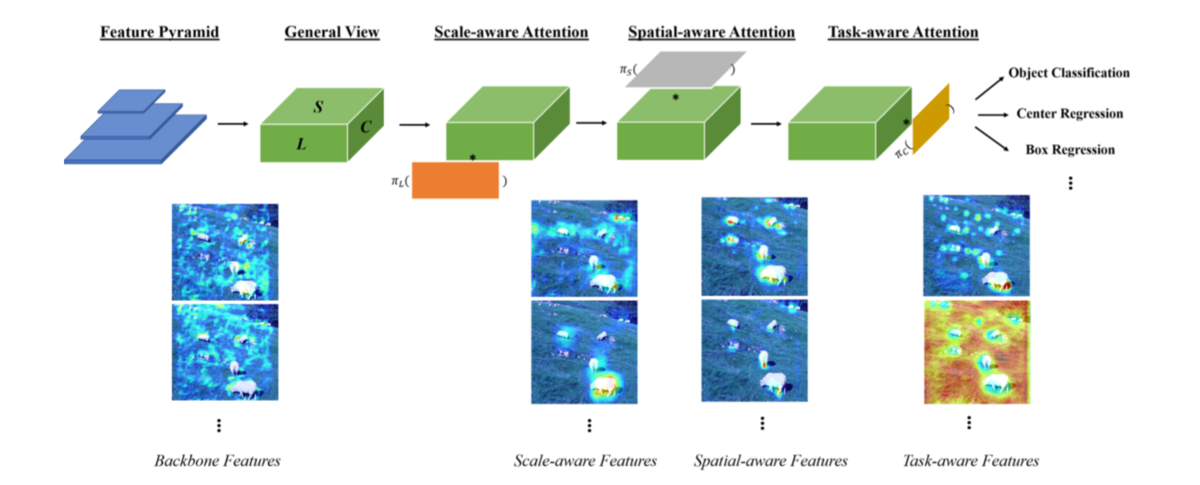
第二パラグラフでは、object detection headの開発にあたっての三つのカテゴリについて記載されており、scale-aware、spatial-aware、task-awareについて紹介されています。詳しくは2-2節で後述しますが、scale-awareはSSDなどで用いられるような異なるサイズのFeature mapの取り扱いについて、spatial-awareは画像上の位置配置について、task-awareはbounding boxやcorner pointsなどのタスクごとの取り扱いについてそれぞれ考えるとされています。


第三パラグラフでは、この論文で紹介するdynamic headではscale-awareness、spatial-awareness、task-awarenessを同時に取り扱うことについて言及されています。それぞれをbackboneネットワークの出力(VGGNetやResNetを用いて作成したFeature mapと同義)をlevel(scale-awareness)、space(spatial-awareness)、channel(task-awareness)の三つの次元を持った3次元テンソルで表すとされています。また、これら三つのawarenessを同時にself-attentionを用いて取り扱うと計算コストがかかるため望ましくないと記載があり、第四パラグラフではその解決にあたってそれぞれを分けて取り扱うことについて言及されています。


第五パラグラフでは行われた実験におけるパフォーマンスに関して記載されています。
2. 論文の重要なポイントの抜粋
2節ではSection2以降の論文の重要なポイントを抜粋して確認します。
2-1 Related Work(Section2)
Section2のRelated Workでは、Scale-awareness、Spatial-awareness、Task-awarenessに関する関連研究についてそれぞれまとめられています。関連研究なので、簡単に流しつつ確認を行います。

(中略)
Scale-awarenessの関連研究でFeature Pyramid Networkが紹介されているので、同様のイメージで考えておくと良いと思います。

(中略)
Spatial-awarenessでは、13がResNet、14がAlexNetの論文のため、基本的なCNNのように空間的な処理を取り扱うと把握しておけば良さそうです。

(中略)
Task-awarenessでは、two-stageとone-stageのトピックなどが紹介されています。23がFaster R-CNN、22がYOLO(You only look once)をそれぞれ参照しています。
2-2 Our Approach(Section3)
Section3のOur ApproachではDynamic Headの研究の仕組みなどについてまとめられています。

上記はSection3-1の記載ですが、Feature mapを元にDynamic Headで用いる特徴量について、数式を用いた記載が行われています。
数式を図にするとFigure.1の左上の上図のようになります。ここで注意が必要なのが、Feature Pyramidでは各Feature mapのサイズが異なるので、それぞれに関してリサイズを行う必要があるということです。また、の4次元テンソルでは直感的に理解するのが難しいことから、
を導入し、
の3次元テンソルに変形を行うことについても把握しておく必要があります。

続くSection3-2では、self-attentionの一般的な数式定義について取り扱われています。ここでがattention関数を表すとされており、全結合層(fully connected layer)がattentionに基づくシンプルな手法であると記載されています。一方で単に全結合層(fully connected layer)を用いるだけでは多次元テンソルの処理は計算負荷が大きく、実用的ではないとも記載がなされています。

計算コストの問題の解決にあたって、attentionを三つの連続したattentionの、
、
にわけることについて試みたとされています。これを受けてそれぞれの処理が記載されます。

まずですが、上記のようにattentionが表されています。先にSとCに関しては和を計算し、それぞれの長さで割ることで平均を計算し、
に関するattentionを行うと理解すれば良いと思います。

次にですが、上記のように表現されています。数式定義が唐突にも見えますが、Deformable Convolutional Networksの記法にある程度基づいているのでこちらも合わせて参照すると良いです。
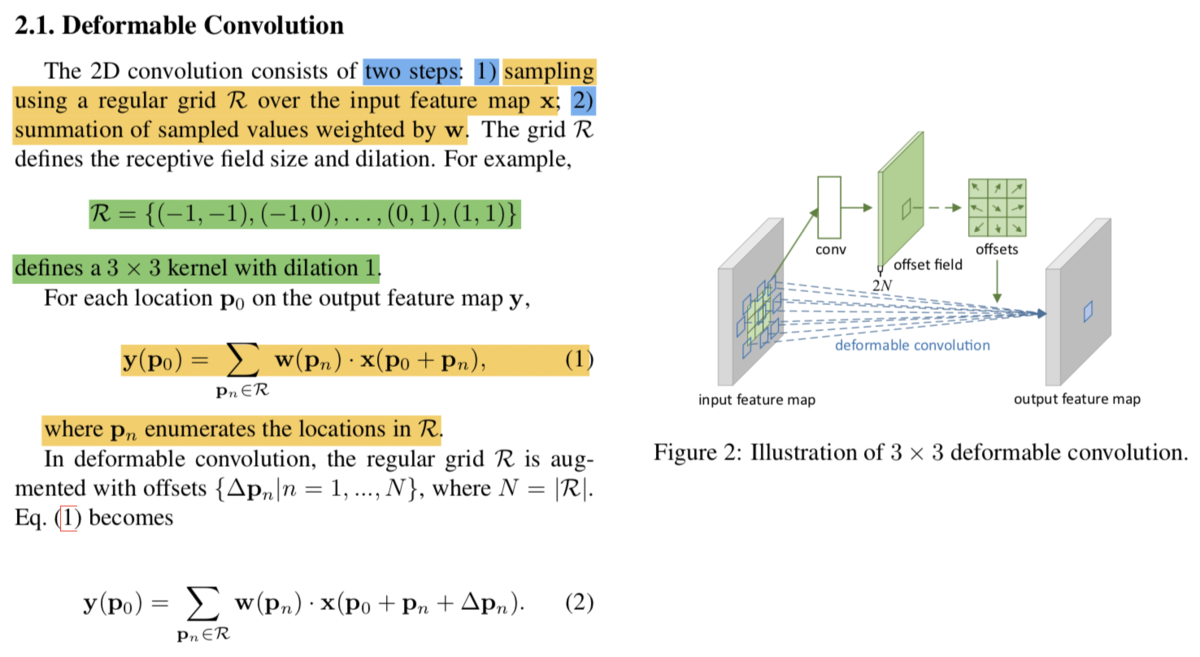
(Deformable Convolutional Networks論文より)

については上記のように記載されています。
2-3 Experiment(Section4)
当記事では省略します。
3. まとめ
#6ではDynamic Head[2021]について取り扱いました。Transformerのようにself-attentionに基づく手法は今後も色々と出てくると思われるので、抑えておくと良さそうでした。
定積分の概要の確認|定積分と積分の応用を把握する #1

上記シリーズで積分の計算について取り扱いましたが、不定積分を中心に積分演算を確認しました。どちらかというと式変形に重きを置きましたが、長さや面積、体積などの計算や、確率分布の正規化など、積分の応用について考えるにあたっては定積分も把握すると良いです。
そこで当シリーズでは、主に定積分を用いた積分の応用について確認を行います。どちらかというと応用例に重きをおいて確認を行えればと思います。
#1では基本事項の確認にあたって、定積分の演算の概要について簡単に確認します。
以下目次になります。
1. 定積分と面積
2. 定積分と符号
3. まとめ
1. 定積分と面積
1節では「定積分と面積」について取り扱います。まず具体的に例を用いて考えるにあたって<
<
の区間において、
と
軸に囲まれる領域の面積を求めるとします。
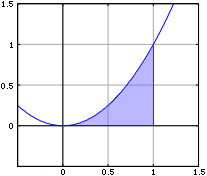
(高等学校数学III/積分法 - Wikibooks より)
ここで、計算は上記の定積分で表すことができます。これを計算すると下記のようになります。
このように、関数と軸で囲まれた領域の面積を求めることができます。
以下、下記の定積分について確認を行います。
1)
2)
3)
4)
5)
計算結果は下記のようになります。
1)
2)
3)
4)
5)
結果の解釈にあたっては、1)〜3)はと基本的に同様ですが、
の次数が大きい方が
<
<
の区間では面積が小さくなることも同時に抑えておくと良いと思います。また、1)は
であり、三角形の面積の公式と対応づけることも可能です。
4)は1)と同様に台形の面積の公式と対応づけることができますが、ここで注意しておくと良いのが5)の結果がとなることです。定積分は基本的に面積と対応しますが、関数の値が
軸よりも下にある場合は符号も考慮しなければならないことは抑えておきましょう。
定積分と符号に関しては続く2節で取り扱うので、1節はここまでとします。
2. 定積分と符号
2節では1節の計算例の5)で出てきたようなケースを題材に定積分と符号について確認します。定積分は関数と軸で囲まれている部分の面積を表しますが、関数の符号には注意が必要です。具体的には関数が負の値を取る区間の積分は絶対値が面積と一致する負の値となります。
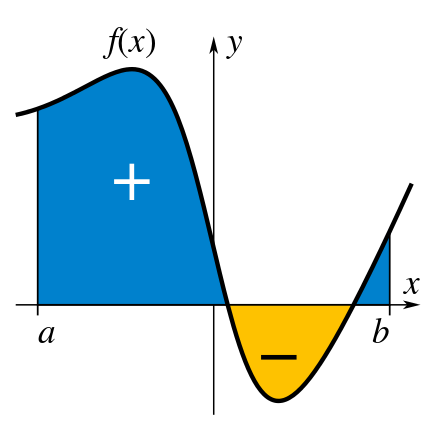
(積分法 - Wikipedia より)
上記はWikipediaの図ですが、こちらのイメージで掴むとわかりやすいです。