$\displaystyle u = g(x)$ とし、両辺を $x$ で微分すると下記のようになります。
$\displaystyle \frac{du}{dx} = g'(x)$
この両辺に $dx$ をかけると下記になります。
$\displaystyle du = g'(x)dx$
ここで $\displaystyle \int f(u) du$ に $\displaystyle du = g'(x)dx$ を代入することで、下記を得ることができます。
$\displaystyle \int f(u) du = \int f(u)g'(x) dx$
$\displaystyle \int f(g(x)) dg(x) = \int f(g(x))g'(x) dx$
$\displaystyle \int f(g(x))g'(x) dx = \int f(g(x)) dg(x)$

これにより置換積分法の式を導出することができました。

置換積分法の概要についてつかめたので1節はここまでとします。

2. 置換積分法の利用例
2節では部分積分法の利用例について確認します。具体的には下記の例題を解くことで部分積分法を確認します。

1) $\displaystyle \int (x+1)^2 dx$
2) $\displaystyle \int (2x+1)^3 dx$

それぞれの部分積分法を用いた計算結果は下記のようになります。

1) $\displaystyle \int (x+1)^2 dx$
$t=x+1$ とおくと $\displaystyle \frac{dx}{dt} = 1$ となる。よって、下記のように計算できる。
$\displaystyle \int (x+1)^2 dx = \int t^2 \frac{dx}{dt} dt$
$\displaystyle = \int t^2 dt$
$\displaystyle = \frac{1}{3}t^3 + C$
$\displaystyle = \frac{1}{3}(x+1)^3 + C$

2) $\displaystyle \int (2x+1)^3 dx$
$t=2x+1$ とおくと $\displaystyle \frac{dx}{dt} = \frac{1}{2}$ となる。よって、下記のように計算できる。
$\displaystyle \int (2x+1)^3 dx = \int t^3 \frac{dx}{dt} dt$
$\displaystyle = \frac{1}{2}\int t^3 dt$
$\displaystyle = \frac{1}{8}t^4 + C$
$\displaystyle = \frac{1}{8}(2x+1)^4 + C$

上記のようにそれぞれの積分を計算することができます。簡単な活用例について確認できたので2節はここまでとします。

3. まとめ
#4では置換積分法について取り扱いました。
引き続き#5では置換積分法について確認します。

2021-06-28

基本関数の積分③（部分積分法）｜様々な積分の計算方法をマスターする #3

Math

f:id:lib-arts:20210618183529p:plain

高等学校数学III 積分法/演習問題 - Wikibooks

#1では基本的な三角関数の積分について、#2では指数関数・対数関数の積分について取り扱いました。

#3では#2の対数関数の積分でも出てきた部分積分法について取り扱います。下記を参考に進めます。

高等学校数学III/積分法 - Wikibooks

以下目次になります。
1. 部分積分法の概要と導出
2. 部分積分法の利用例
3. まとめ

1. 部分積分法の概要と導出
1節では部分積分法の概要と導出について取り扱います。

高等学校数学III/積分法 - Wikibooks

上記を主に参考にします。

まず部分積分法を表す一般的な数式から確認します。

$\displaystyle \int f(x)g'(x) dx = f(x)g(x) - \int f'(x)g(x) dx$

上記の数式だと具体的なイメージがわかないと思うので簡単な具体例を確認しますが、 $f(x)=x$ 、 $g(x)=\sin{x}$ のように、 $f(x)$ が微分した際に定数となる場合などに部分積分法が活用できます。 $f(x)=x$ 、 $g(x)=\sin{x}$ の場合は $f'(x)g(x)=\sin{x}=g(x)$ となり、#1で取り扱った三角関数の積分の考え方を用いて積分を行うことが可能です。

ここまでで部分積分法の概要がつかめたと思いますので、以下部分積分法の導出について取り扱います。部分積分法の導出にあたっては基本的に「積の導関数」の式から導出します。

$\displaystyle (f(x)g(x))' = f'(x)g(x)+f(x)g'(x)$
上記の積の導関数の式の両辺を積分します。
$\displaystyle \int (f(x)g(x))' dx = \int (f'(x)g(x)+f(x)g'(x)) dx$
$\displaystyle \int (f(x)g(x))' dx = \int f'(x)g(x) dx + \int f(x)g'(x)) dx$
これを変形することで下記の部分積分法の式が導出できます。
$\displaystyle \int f(x)g'(x) dx = f(x)g(x) - \int f'(x)g(x) dx$

部分積分法の概要と導出について確認できたので1節はここまでとします。

2. 部分積分法の利用例
2節では部分積分法の利用例について確認します。具体的には下記の例題を解くことで部分積分法を確認します。

1) $\displaystyle \int x\sin{x} dx$
2) $\displaystyle \int xe^x dx$
3) $\displaystyle \int x^2e^x dx$

それぞれの部分積分法を用いた計算結果は下記のようになります。

1) $\displaystyle \int x\sin{x} dx$
$\displaystyle \int x\sin{x} dx = \int x(-\cos{x})' dx$
　　 $\displaystyle = x(-\cos{x}) - \int x'(-\cos{x}) dx$
　　 $\displaystyle = -x\cos{x} + \int \cos{x} dx$
　　 $\displaystyle = -x\cos{x} + \sin{x} +C$

2) $\displaystyle \int xe^x dx$
$\displaystyle \int xe^x dx = \int x(e^x)' dx$
　　 $\displaystyle = x(e^x) - \int x'(e^x) dx$
　　 $\displaystyle = xe^x + \int e^x dx$
　　 $\displaystyle = xe^x + e^x +C$

3) $\displaystyle \int x^2e^x dx$
$\displaystyle \int x^2e^x dx = \int x^2(e^x)' dx$
　　 $\displaystyle = x^2(e^x) - \int (x^2)'(e^x) dx$
　　 $\displaystyle = x^2e^x - \int 2xe^x dx$
　　 $\displaystyle = x^2e^x - 2\int x(e^x)' dx$
　　 $\displaystyle = x^2e^x - 2xe^x + 2\int x'e^x dx$
　　 $\displaystyle = x^2e^x - 2xe^x + 2\int e^x dx$
　　 $\displaystyle = x^2e^x - 2xe^x + 2e^x + C$
　　 $\displaystyle = (x^2-2x+2)e^x + C$

上記のようにそれぞれの積分は計算することができます。部分積分の基本的な活用例について確認できたので2節はここまでとします。

3. まとめ
#3では部分積分法について取り扱いました。
#4では部分積分法と同様に積分にあたって用いられる置換積分法について取り扱います。

2021-06-27

基本関数の積分②（指数関数・対数関数の積分）｜様々な積分の計算方法をマスターする #2

Math

f:id:lib-arts:20210618183529p:plain

高等学校数学III 積分法/演習問題 - Wikibooks

#1では基本的な三角関数の積分について取り扱いました。

#2では指数関数・対数関数の積分について取り扱います。

以下目次になります。
1. 指数関数の積分
2. 対数関数の積分
3. まとめ

1. 指数関数の積分
1節では指数関数の積分について取り扱います。

高等学校数学III/積分法 - Wikibooks

主に上記を参考にします。
まずは $e^x$ の積分から確認します。

$\displaystyle \int e^x dx = \int (e^x)' dx$
　　 $\displaystyle = e^x+C$

$e^x$ は上記のように計算できます。

次に $a$ ＞ $0$ である $a^x$ の積分について確認します。 $a=e^{\log_e{a}}$ であることを利用します。

$\displaystyle \int a^x dx = \int e^{\log_{e}a x} dx$
　　 $\displaystyle = \int \left( \frac{1}{\log_e{a}}e^{\log_e{a}x} \right)' dx$
　　 $\displaystyle = \frac{1}{\log_e{a}}\int \left( e^{\log_e{a}x} \right)' dx$
　　 $\displaystyle = \frac{e^{\log_e{a}x}}{\log_e{a}} + C$
　　 $\displaystyle = \frac{a^x}{\log_e{a}} + C$

$a=e^{\log_e{a}}$ のような変換は一見難しそうに見えますが、対数関数の定義からそのまま考えただけでそれほど難しくありません（ $e$ を $\log_e{a}$ 乗すれば $a$ になるというところから対数 $\log_e{a}$ が定義されます）。

指数関数の積分について取り扱えたので1節はここまでとします。

2. 対数関数の積分
2節では対数関数の積分について取り扱います。

高等学校数学III/積分法 - Wikibooks

主に上記を参考にします。
以下では $\log{|x|}=\log_e{|x|}$ の積分について確認します。（部分積分が出てくるので詳しくは#3の記事で確認します）

$\displaystyle \int \log{|x|} dx = \int (x)'\log{|x|} dx$
　　 $\displaystyle x\log{|x|} - \int x(\log{|x|})' dx$
　　 $\displaystyle x\log{|x|} - \int x\frac{1}{x} dx$
　　 $\displaystyle x\log{|x|} - \int 1 dx$
　　 $\displaystyle x\log{|x|} - x + C$

部分積分が出てきて少々複雑になりますが、対数関数の積分は上記のように計算できます。

対数関数の積分について取り扱えたので2節はここまでとします。

3. まとめ
#2では指数関数・対数関数の積分について取り扱いました。
#3では2節でも出てきた手法である部分積分法について取り扱います。

2021-06-26

基本関数の積分①（三角関数の積分）｜様々な積分の計算方法をマスターする #1

Math

f:id:lib-arts:20210618183529p:plain

数Ⅱ以降、数多くの分野で用いられる積分ですが、計算が複雑になるとなかなか取り扱いが難しいです。特に置換積分のように発見的な解法が用いられることもあり、ある程度把握しておかないととできない積分なども多い印象です。
そこで当シリーズでは主に数Ⅲ〜大学教養レベルにかけての積分の中から基本トピックではある一方で比較的複雑な積分を取り扱うこととします。具体的には下記などがスムーズに解けるというのを目安に進めたいと思います。

高等学校数学III 積分法/演習問題 - Wikibooks

#1では基本的な三角関数の積分について取り扱います。

以下目次になります。
1. $\sin{x}$ 、 $\cos{x}$ を用いた関数の積分
2. $\tan{x}$ を用いた関数の積分
3. まとめ

1. $\sin{x}$ 、 $\cos{x}$ を用いた関数の積分
1節では $\sin{x}$ 、 $\cos{x}$ の積分について取り扱います。下記を主に参考にします。

高等学校数学III/積分法 - Wikibooks

$\sin{x}$ 、 $\cos{x}$ を考えるにあたっては、下記の三角関数に関する微分の逆演算を考えると良いです。

$\displaystyle (\sin{x})' = \cos{x}$
$\displaystyle (\cos{x})' = -\sin{x}$
$\displaystyle (\tan{x})' = \frac{1}{\cos^2{x}}$

上記が成立することを考慮して、下記が導出できます。

$\displaystyle \int \cos{x} dx = \sin{x}+C$
$\displaystyle \int \sin{x} dx = -\cos{x}+C$
$\displaystyle \int \frac{1}{\cos^2{x}} dx = \tan{x}+C$

ここまでで $\sin{x}$ 、 $\cos{x}$ を用いた関数の積分について確認できたので1節はここまでとします。

2. $\tan{x}$ を用いた関数の積分
2節では $\tan{x}$ の積分について取り扱います。下記を主に参考にします。

高等学校数学III/積分法 - Wikibooks

$\tan{x}$ の積分は合成関数の微分の逆演算で求めることができると考えておくと良いです。

$\displaystyle \int \tan{x} dx = \int \frac{\sin{x}}{\cos{x}} dx$
　　 $\displaystyle = \int \frac{-(\cos{x})'}{\cos{x}} dx$
　　 $\displaystyle = -\log{|\cos{x}|}+C$

この時 $\displaystyle \frac{1}{x}$ の積分演算を行う際は $-\log{|x|}+C$ のように絶対値をつけることに注意しておくと良いです。（詳しく考えると色々な見方があるかと思いますが、当記事では一旦慣例的にこのように用いるとできればと思います）

3. まとめ
#1では基本的な三角関数に関連する積分について取り扱いました。
#2では指数関数・対数関数の積分について取り扱います。

2021-06-25

円錐曲線と離心率｜式と曲線を把握する #5

Math

f:id:lib-arts:20210618183529p:plain

数学Cや基本的な解析学で取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#4では双曲線関数について取り扱いました。

#5では#1〜#3までで取り扱った楕円、放物線、双曲線などを総称した円錐曲線(conic curve)と離心率(eccentricity)について取り扱います。主に下記を参考にします。

円錐曲線 - Wikipedia

以下当記事の目次になります。
1. 円錐曲線について
2. 離心率について
3. まとめ

1. 円錐曲線について
1節では円錐曲線(conic curve)について簡単に確認します。

円錐曲線 - Wikipedia

上記を主に参考にします。円錐曲線は「円錐面を任意の平面で切断したときの断面としてえられる曲線群の総称」とされます。
$xy$ 平面上の円錐曲線の数式は下記のようになります。

$P(x,y)=c_1x^2+2c_2xy+c_3y^2+2c_4x+2c_5y+c_6=0$ ...①

よって任意の二次式の $P(x,y)$ に関して $P(x,y)=0$ が円錐曲線となり、このことから円錐曲線は二次曲線とも言われます。以下、円錐曲線の定義に基づいて具体的な曲線について確認を行います。

・円
$x^2+y^2=r^2$
①において、 $c_1=c_3=1$ 、 $c_2=c_4=c_5=0$ 、 $c_6=-r^2$ とすることによって導出できる。

・楕円
$\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$
①において、 $c_1=b^2$ 、 $c_3=a^2$ 、 $c_2=c_4=c_5=0$ 、 $c_6=-a^2b^2$ とすることによって導出できる。

・放物線
$x^2 = 4cy$ 、 $y^2 = 4cx$
$x^2 = 4cy$ は①において $c_1=1$ 、 $c_5=-4c$ 、 $c_2=c_3=c_4c_6=0$ とすることによって導出できる。 $y^2 = 4cx$ も同様に考えることで導出できる。

・双曲線
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1$

①において、 $c_1=b^2$ 、 $c_3=-a^2$ 、 $c_2=c_4=c_5=0$ 、 $c_6=\pm a^2b^2$ とすることによって導出できる。

・二直線
$\displaystyle ax^2 - by^2 = 0$
①において、 $c_1=a$ 、 $c_3=-b$ 、 $c_2=c_4=c_5=c_6=0$ とすることによって導出できる。

また、円と二直線に関しては円錐曲線に含まない場合もあることに注意しておくと良いです。（円は円錐曲線に含み、二直線は含まないことが多いようです）

円錐曲線（二次曲線）について簡単に確認できたので1節はここまでとします。

2. 離心率について
2節では離心率(eccentricity)について簡単に確認します。

円錐曲線 - Wikipedia

上記を主に参考にします。

f:id:lib-arts:20210624185408p:plain

（円錐曲線 - Wikipedia より）
上図のように直線(準線)と点(焦点)を定める時に、 $FM:MM' = e:1$ ( $e$ ＞ $0$ )を考えると、 $e$ が離心率を表します。このとき、 $M$ の集合は円錐曲線を描きます。
また、離心率 $e$ と描かれる円錐曲線の概形の関係は以下のようになります。

・ $0$ ＜ $e$ ＜ $1$ ：楕円
・ $e = 1$ ：放物線
・ $e$ ＞ $1$ ：双曲線

離心率の概要について確認できたので2節はここまでとします。

3. まとめ
#5では円錐曲線と離心率について確認しました。
#6では惑星の運動について取り扱うケプラーの法則について取り扱います。

ケプラーの法則 - Wikipedia

2021-06-24

双曲線関数の概要を確認する（解析学基礎）｜式と曲線を把握する #4

Math

f:id:lib-arts:20210618183529p:plain

数学Cなどで取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#1〜#3では「楕円」、「放物線」、「双曲線」の方程式とその導出について取り扱いました。

#4では#3の「双曲線」に関連して「双曲線関数」について取り扱います。主に下記を参考にします。

解析学基礎/双曲線関数 - Wikibooks

以下当記事の目次になります。
1. 双曲線関数とその概要について
2. 双曲線関数を用いた双曲線の描画
3. まとめ

1. 双曲線関数とその概要について
1節では「双曲線関数」とその概要について取り扱います。まずは双曲線関数の定義から確認します。

$\displaystyle \sinh{x} = \frac{e^x-e^{-x}}{2}$
$\displaystyle \cosh{x} = \frac{e^x+e^{-x}}{2}$

上記が双曲線関数の定義ですが、sinhはハイパーボリックサイン(hyperbolic sine)、coshはハイパーボリックコサイン(hyperbolic cosine)の略を意味します。

式の定義について確認できたので、次に双曲線関数の性質について確認します。

$\displaystyle \cosh^{2}{x} - \sinh^{2}{x} = 1$ ...①
$\displaystyle \sinh{(a+b)} = \sinh{a}\cosh{b}+\cosh{a}\sinh{b}$ ...②
$\displaystyle \cosh{(a+b)} = \cosh{a}\cosh{b}+\sinh{a}\sinh{b}$ ...③
$\displaystyle \frac{d}{dx}\sinh{x} = \cosh{x}$ ...④
$\displaystyle \frac{d}{dx}\cosh{x} = \sinh{x}$ ...⑤

上記はどれも三角関数に似た性質を持つので三角関数と同様の記号が用いられています。また、①の性質より、 $(x,y) = (\cosh{t},\sinh{t})$ のように双曲線関数を用いて双曲線上の点を表すことができます。これは通常の三角関数が $(x,y) = (\cos{t},\sin{t})$ のように単位円上の点を表すことができることと対応づけておくと良いです。

双曲線関数の式定義と簡単な性質について把握できたので1節はここまでとします。

2. 双曲線関数を用いた双曲線の描画
2節では双曲線関数を用いた双曲線の描画について取り扱います。1節でも簡単に取り扱いましたが、①の式が成立することの確認や具体的に双曲線を描画することで、双曲線関数について把握できればと思います。まずは①の式が成立することを確認します。

$\displaystyle \cosh^{2}{x} - \sinh^{2}{x} = \left( \frac{e^x+e^{-x}}{2} \right)^2 - \left( \frac{e^x-e^{-x}}{2} \right)^2$
　　 $\displaystyle = \frac{e^{2x}+2e^xe{-x}+e^{-2x}}{4} - \frac{e^{2x}-2e^xe{-x}+e^{-2x}}{4}$
　　 $\displaystyle = \frac{4e^xe{-x}}{4}$
　　 $\displaystyle = \frac{4}{4}$
　　 $= 1$

上記より①の式が成立することが確認できました。

次に、 $(x,y) = (\cosh{t},\sinh{t})$ のように双曲線関数を用いて双曲線の描画を行います。ここでは概要を掴むにあたって $=-2,-1,0,1,2$ の値を計算し、グラフを描画します。

・ $t=-2$
$\displaystyle (\cosh{-2},\sinh{-2}) = (\frac{e^{-2}+e^{2}}{2},\frac{e^{-2}-e^{2}}{2})$
　　 $= (3.762195691083631, -3.6268604078470186)$

・ $t=-1$
$\displaystyle (\cosh{-1},\sinh{-1}) = (\frac{e^{-1}+e^{1}}{2},\frac{e^{-1}-e^{1}}{2})$
　　 $= (1.5430806348152437, -1.1752011936438014)$

・ $t=0$
$\displaystyle (\cosh{0},\sinh{0}) = (\frac{e^{0}+e^{0}}{2},\frac{e^{0}-e^{0}}{2})$
　　 $= (1, 0)$

・ $t=1$
$\displaystyle (\cosh{1},\sinh{1}) = (\frac{e^{1}+e^{-1}}{2},\frac{e^{1}-e^{-1}}{2})$
　　 $= (1.5430806348152437, 1.1752011936438014)$

・ $t=2$
$\displaystyle (\cosh{2},\sinh{2}) = (\frac{e^{2}+e^{-2}}{2},\frac{e^{2}-e^{-2}}{2})$
　　 $= (3.762195691083631, 3.6268604078470186)$

計算結果から $(x,y)=(1,0)$ を通り、徐々に $x$ と $y$ の値が近づくことから双曲線が描けそうだということが確認できます。

また、以下ではPythonでの描画で確認してみます。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

t1 = np.arange(-2,2.1,0.1)
t2 = np.arange(-2,3,1)

plt.plot( (np.e**(t1)+np.e**(-t1) )/2., (np.e**(t1)-np.e**(-t1))/2., color="limegreen")
plt.scatter( (np.e**(t2)+np.e**(-t2) )/2., (np.e**(t2)-np.e**(-t2))/2.)

plt.show()

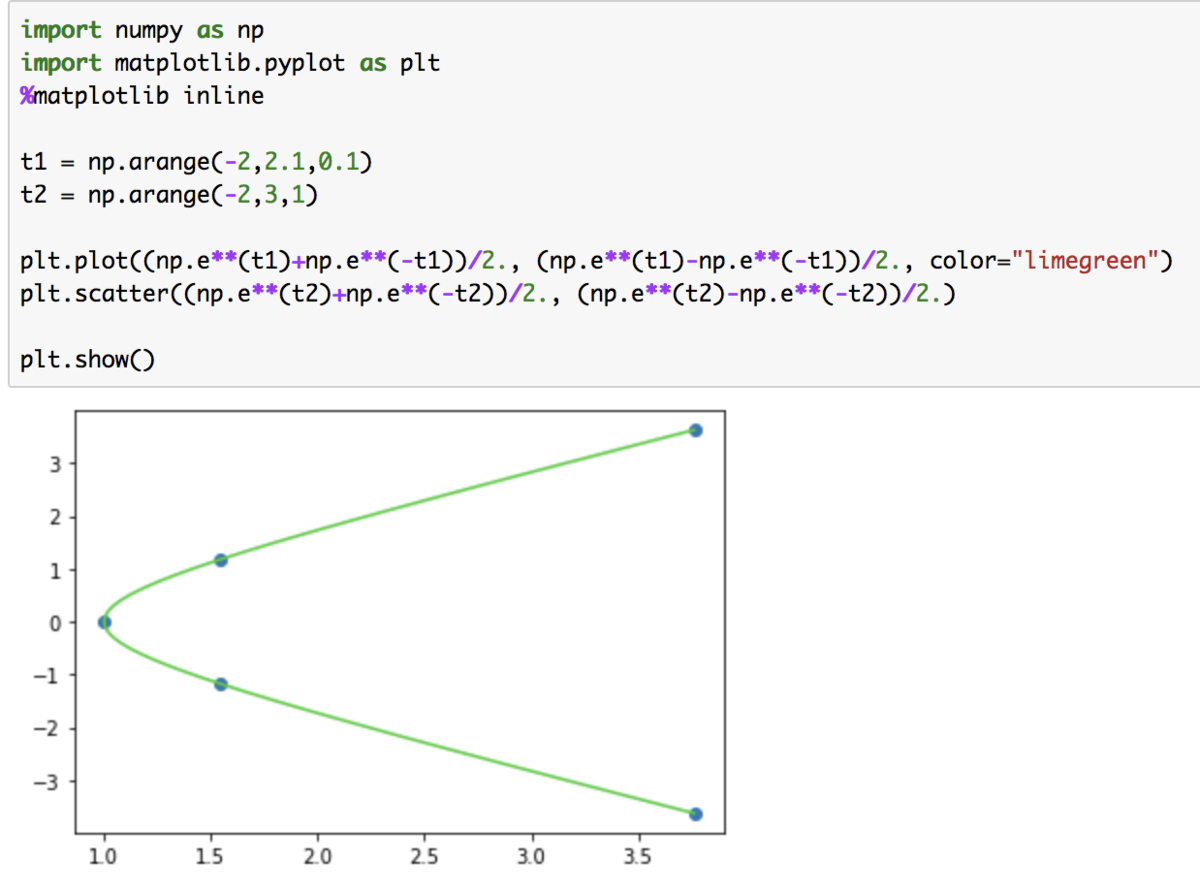
f:id:lib-arts:20210623171602p:plain

上記のように、グラフが確認できます。また、 $(x,y) = (\pm \cosh{t},\sinh{t})$ を考慮することで反対側も同時に描画できます。

f:id:lib-arts:20210623171623p:plain

上図が双曲線のグラフの描画にあたって紹介されることが多いと思います。

双曲線関数を用いた双曲線の描画について取り扱えたので2節はここまでとします。

3. まとめ
#4では解析学の基礎より双曲線関数の概要を確認しました。
#5では下記を参考に円錐曲線と離心率について取り扱います。

円錐曲線 - Wikipedia

2021-06-23

双曲線の方程式と導出｜式と曲線を把握する #3

Math

f:id:lib-arts:20210618183529p:plain

数学Cなどで取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#1では「楕円」の方程式と導出、#2では「放物線」の方程式と導出について取り扱いました。

#3では「双曲線」の方程式と導出について取り扱います。主に下記を参考に進めます。

高等学校数学C/式と曲線 - Wikibooks

以下当記事の目次になります。
1. 双曲線の方程式とその概要
2. 双曲線の方程式の導出
3. まとめ

1. 双曲線の方程式とその概要
1節では「双曲線」の方程式とその概要に関して確認します。まずは双曲線の方程式について確認します。

$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ ①
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1$ ②
（ $a$ と $b$ は正の定数）

上記が双曲線の方程式です。概要を掴むにあたって①について考えます。具体的に考える方がわかりやすいので、 $y=0$ 、 $y=1$ 、 $y=2$ を考え、これに対応する $x$ の値を計算を行うとします。

・ $y=0$ のとき
$\displaystyle \frac{x^2}{a^2} = 1$
$x^2 = a^2$
$a$ ＞ $0$ より $x = \pm a$

・ $y=1$ のとき
$\displaystyle \frac{x^2}{a^2} - \frac{1}{b^2} = 1$
$\displaystyle \frac{x^2}{a^2} = 1+\frac{1}{b^2}$
$\displaystyle \frac{x^2}{a^2} = \frac{b^2+1}{b^2}$
$\displaystyle x^2 = \frac{a^2(b^2+1)}{b^2}$
$a$ ＞ $0$ より $x = \pm \frac{\sqrt{a^2(b^2+1)}}{b}$

・ $y=2$ のとき
$\displaystyle \frac{x^2}{a^2} - \frac{4}{b^2} = 1$
$\displaystyle \frac{x^2}{a^2} = 1+\frac{4}{b^2}$
$\displaystyle \frac{x^2}{a^2} = \frac{b^2+4}{b^2}$
$\displaystyle x^2 = \frac{a^2(b^2+4)}{b^2}$
$a$ ＞ $0$ より $x = \pm \frac{\sqrt{a^2(b^2+4)}}{b}$

$y$ に具体的な数値を入れて確認しましたが、これでもまだ具体的なイメージがつかめないので $a=b=1$ を代入して値を確認することとします。

・ $y=0$ のとき
$x = \pm 1$

・ $y=1$ のとき
$x = \pm \frac{\sqrt{a^2(b^2+1)}}{b}$
　　 $= \pm \frac{\sqrt{1^2(1^2+1)}}{1}$
　　 $= \pm \sqrt{2}$

・ $y=2$ のとき
$x = \pm \frac{\sqrt{a^2(b^2+4)}}{b}$
　　 $= \pm \frac{\sqrt{1^2(1^2+4)}}{1}$
　　 $= \pm \sqrt{5}$

これより、 $\displaystyle x = \sqrt{y^2+1}$ のようなイメージを持つと良いと思います。

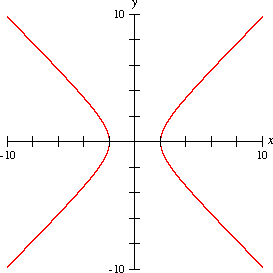
f:id:lib-arts:20210622163617p:plain

（双曲線 - Wikipedia より）
大まかな図は上記のようになります。また、双曲線には2つの漸近線が存在し、それぞれ $bx+ay=0$ 、 $bx-ay=0$ で表すことができます。

双曲線の数式とその概要について大まかに抑えられたので1節はここまでとします。

2. 双曲線の方程式の導出
2節では双曲線の方程式の導出について確認します。双曲線の定義は、「平面状にある2定点(焦点)からの距離の差が一定になるような点の集合からなる曲線」というものです。以下、2つの焦点を $(c,0)$ 、 $(-c,0)$ 、焦点からの距離の差を $2a$ とおき、双曲線の方程式を導出します。

まず、定義より下記が成立します。
$\displaystyle |\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}| = 2a$
$\displaystyle \sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2} = \pm 2a$
$\displaystyle \sqrt{(x-c)^2+y^2} = \sqrt{(x+c)^2+y^2} \pm 2a$
ここで上記の二乗を行います。
$\displaystyle (x-c)^2+y^2 = (x+c)^2+y^2 \pm 4a\sqrt{(x+c)^2+y^2} + 4a^2$
$\displaystyle ((x-c)^2+y^2)-((x+c)^2+y^2+4a^2) = \pm 4a\sqrt{(x+c)^2+y^2}$
$\displaystyle -4(a^2+cx) = \pm 4a\sqrt{(x+c)^2+y^2}$
$\displaystyle -(a^2+cx) = \pm a\sqrt{(x+c)^2+y^2}$
さらに上記の両辺を再度二乗します。
$\displaystyle (a^2+cx)^2 = a^2((x+c)^2+y^2)$
$\displaystyle a^4+2a^2cx+c^2x^2 = a^2(x^2+2cx+c^2+y^2)$
$\displaystyle a^4+2a^2cx+c^2x^2 = a^2x^2+2a^2cx+a^2c^2+a^2y^2$
$\displaystyle a^4+c^2x^2 = a^2x^2+a^2c^2+a^2y^2$
$\displaystyle (c^2-a^2)x^2-a^2y^2 = a^2c^2-a^4$
$\displaystyle (c^2-a^2)x^2-a^2y^2 = a^2(c^2-a^2)$
ここで $b^2=c^2-a^2$ と置き換えます。
$\displaystyle b^2x^2-a^2y^2 = a^2b^2$
さらにここで両辺を $a^2b^2$ で割ります。
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$
上記が楕円の方程式に一致します。