2021-05-31

対数関数の微分｜基本関数の微分の公式を定義から導出する #2

Math

f:id:lib-arts:20210213195311p:plain

指数関数、対数関数、三角関数などの微分の公式を定義から導出を行うシリーズです。#1では指数関数の微分について取り扱いました。

#2では対数関数の微分に関して取り扱いたいと思います。

以下、目次になります。
1. $f(x)=\log_{e}{x}$ の微分の導出
2. $f(x)=\log_{a}{x}$ の微分の導出
3. まとめ

1. $f(x)=\log_{e}{x}$ の微分の導出
1節では $f(x)=\log_{e}{x}$ の微分の導出について確認します。まずは微分の定義式と比較しながら式を確認します。

$\displaystyle f'(x) = \lim_{h \to +0} \frac{f(x+h)-f(x)}{(x+h)-h}$
　　 $\displaystyle = \lim_{h \to +0} \frac{\log_{e}{(x+h)}-\log_{e}{x}}{h}$
　　 $\displaystyle = \lim_{h \to +0} \frac{1}{h}\log_{e}\left(\frac{x+h}{x}\right)$
　　 $\displaystyle = \lim_{h \to +0} \frac{1}{h}\log_{e}\left(1+\frac{h}{x}\right)$
　　 $\displaystyle = \lim_{h \to +0} \frac{1}{x}\frac{x}{h}\log{e}\left(1+\frac{h}{x}\right)$

上記の数式において $\displaystyle k = \frac{x}{h}$ とすると、 $\displaystyle \frac{h}{x} = \frac{1}{k}$ 、 $h \to +0$ のとき $k \to \infty$ なので下記のように変形できます。

$\displaystyle = \lim_{h \to +0} \frac{1}{x}\frac{x}{h}\log_{e}\left(1+\frac{h}{x}\right) = \lim_{k \to \infty} \frac{1}{x}k\log_{e}\left(1+\frac{1}{k}\right)$
　　 $\displaystyle = \frac{1}{x} \lim_{k \to \infty} \log_{e}\left(1+\frac{1}{k}\right)^k$
　　 $\displaystyle = \frac{1}{x} \log_{e}{e}$
　　 $\displaystyle = \frac{1}{x}$

ここまでの議論より、 $\displaystyle (\log_{e}{x})' = \frac{1}{x}$ が成立することがわかります。

2. $f(x)=\log_{a}{x}$ の微分の導出
2節では $f(x)=\log_{a}{x}$ の微分の導出について確認します。底の変換公式を用いると $\log_{a}{x}$ は下記のように変換できます。

$\displaystyle \log_{a}{x} = \frac{\log_{e}{x}}{\log_{e}{a}}$

よって、 $(\log_{a}{x})'$ は下記のように計算できます。

$\displaystyle (\log_{a}{x})' = \left(\frac{\log_{e}{x}}{\log_{e}{a}}\right)'$
　　 $\displaystyle = \frac{1}{\log_{e}{a}}(\log_{e}{x})'$
　　 $\displaystyle = \frac{1}{\log_{e}{a}}\frac{1}{x}$
　　 $\displaystyle = \frac{1}{x\log_{e}{a}}$

よって $\displaystyle (\log_{a}{x})' = \frac{1}{x\log_{e}{a}}$ が成立することがわかります。

3. まとめ
#2では対数関数の定義に基づく微分について確認しました。
#3では同様に三角関数の定義に基づく微分について確認します。

2021-05-30

指数関数の微分｜基本関数の微分の公式を定義から導出する #1

Math

f:id:lib-arts:20210213195311p:plain

微積分は数Ⅱ数Ⅲにおける重要なトピックですが、定義からの導出が比較的容易な数Ⅱの微分に対して、数Ⅲの微分はなかなか複雑です。そこで当シリーズでは基本関数の微分の公式を定義から導出を行えればと思います。
基本的には指数関数、対数関数、三角関数などを取り扱えればと思います。#1では指数関数の微分について取り扱います。

以下、目次になります。
1. $f(x)=e^x$ の微分の導出
2. $f(x)=a^x$ の微分の導出
3. まとめ

1. $f(x)=e^x$ の微分の導出
1節では $f(x)=e^x$ の微分の導出について取り扱います。

基本的な方針は上記の1節の $e$ のオイラーによる定義と類似の変形を行います。まず準備として、 $f(x)=e^x$ とした上で、微分の定義式に基づいて導関数を考えます。

$\displaystyle f'(x) = \lim_{h \to +0} \frac{f(x+h)-f(x)}{(x+h)-h} = \lim_{h \to +0} \frac{e^{x+h}-e^x}{h}$

上記の分子において、 $e^{x+h}-e^x = e^x(e^h-1)$ が成立し、 $e^x$ が $h$ と関係ないことから下記のように変形できます。

$\displaystyle f'(x) = e^x \lim_{h \to +0} \frac{e^h-1}{h}$ (1)

$(e^x)'=e^x$ なので、 $\displaystyle \lim_{h \to +0} \frac{e^h-1}{h} = 1$ を示すのが以下での目標になります。（オイラーの定義では $e$ がこの式を満たすように設定するとされますが、ここでは $\displaystyle \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e$ のみを用いることができるとします。
また、 $\displaystyle \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e$ において $\displaystyle n_{inv} = \frac{1}{n}$ とすることで、

$\displaystyle \lim_{n_{inv} \to +0} (1 + n_{inv})^{\frac{1}{n_{inv}}} = e$ (2)

を導出することもできます。

さて、(1)式だけだとわかりにくいため、 $k=e^h-1$ となる $k$ を導入し、以後変形を行います（ここで $h \to +0$ のとき、 $k \to e^0-1 = +0$ となります）。また、 $k=e^h-1$ を $h$ について解くと $h=\log(k+1)$ のようになります。
ここまでの議論により、(1)の分子を $e^h-1=k$ 、分母を $h=\log(k+1)$ で置き換えると下記のようになります。

$\displaystyle \frac{e^h-1}{h} = \frac{k}{\log(k+1)}$
　　 $\displaystyle = \frac{1}{\frac{1}{k}\log(k+1)}$
　　 $\displaystyle = \frac{1}{\log(1+k)^{\frac{1}{k}}}$

ここで $\displaystyle \lim_{k \to +0} \log(1+k)^{\frac{1}{k}}$ は(2)式と同じ式のため、値は $e$ になります。よって $\displaystyle \lim_{k \to +0} \frac{1}{\log(1+k)^{\frac{1}{k}}} = \frac{1}{\log{e}} = 1$ が計算できます。

ここまでの議論により、 $\displaystyle f'(x) = e^x$ が成立することがわかります。

2. $f(x)=a^x$ の微分の導出
2節では $f(x)=a^x$ の微分の導出について確認します。基本的には $a^x=e^{\log_e{a}x}$ とできることより導出します。
合成関数の微分を利用することで、 $(e^{\log_e{a}x})'$ は下記のように導出できます。

$(e^{\log_e{a}x})' = \log_e{a}e^{\log_e{a}x} = a^{x} \log_e{a}$

よって、 $(a^x)' = a^{x} \log_e{a}$ が導出できます。

1節と同様に $\displaystyle a^x \lim_{h \to +0} \frac{a^h-1}{h}$ のように変形し、 $\displaystyle \lim_{h \to +0} \frac{a^h-1}{h} = \log_e{a}$ を導出することによって $(a^x)' = a^{x} \log_e{a}$ を導出することもできます。

3. まとめ
#1では指数関数の定義に基づく微分について確認しました。
#2では同様に対数関数の定義に基づく微分について確認します。

2021-05-29

数学検定準1級の問題の解説 #3

Math

f:id:lib-arts:20210213195311p:plain

数学検定準1級の問題の解説を行うシリーズです。基礎的なトピックの確認を行うのが主目的のため、1次試験を中心に取り扱います。問題と解答は下記です。

https://www.su-gaku.net/suken/wp-content/themes/su-ken/pdf/support/past_question/2020/j1q_que_1ji.pdf

https://www.su-gaku.net/suken/wp-content/themes/su-ken/pdf/support/past_question/2020/j1q_ans_1ji.pdf

#1では問題1〜2について、#2では問題3〜4についてそれぞれ取り扱いました。

#3では問題5〜7について取り扱います。

以下、問題5〜7についてそれぞれ確認を行います。

・問題5
① 不定積分 $\displaystyle \int \left(\frac{x^2}{2}+3x\right)e^{\frac{x}{2}} dx$ を求めよ
② 定積分 $\displaystyle \int_{0}^{2} \left(\frac{x^2}{2}+3x\right)e^{\frac{x}{2}} dx$ を求めよ

Answer.
同じ関数について取り扱っているので、①が解ければ②は①で導出した関数を $F(x)$ とした際の $F(2)-F(0)$ とすることで解ける。①の積分にあたっては、部分積分の考え方を用いる。
$\displaystyle \int \left(\frac{x^2}{2}+3x\right)e^{\frac{x}{2}} dx$
　　 $\displaystyle = 2\int \left(\frac{x^2}{2}+3x\right)\left(e^{\frac{x}{2}}\right)' dx$
　　 $\displaystyle = 2\left(\frac{x^2}{2}+3x\right)e^{\frac{x}{2}} - 2\int \left(\frac{x^2}{2}+3x\right)'e^{\frac{x}{2}} dx$
　　 $\displaystyle = 2\left(\frac{x^2}{2}+3x\right)e^{\frac{x}{2}} - 4\int (x+3)\left(e^{\frac{x}{2}}\right)' dx$
　　 $\displaystyle = (x^2+6x)e^{\frac{x}{2}} - 4(x+3)e^{\frac{x}{2}} + 4\int (x+3)'e^{\frac{x}{2}} dx$
　　 $\displaystyle = (x^2+6x)e^{\frac{x}{2}} - 4(x+3)e^{\frac{x}{2}} + 8\int \left(e^{\frac{x}{2}}\right)' dx$
　　 $\displaystyle = (x^2+6x)e^{\frac{x}{2}} - 4(x+3)e^{\frac{x}{2}} + 8e^{\frac{x}{2}} + C$
　　 $\displaystyle = (x^2+6x-4x-12+8)e^{\frac{x}{2}} + C$
　　 $\displaystyle = (x^2+2x-4)e^{\frac{x}{2}} + C$
①の不定積分は上記より、 $\displaystyle \int \left(\frac{x^2}{2}+3x\right)e^{\frac{x}{2}} dx = (x^2+2x-4)e^{\frac{x}{2}} + C$ となる。
また、これより②は
$\displaystyle \int_{0}^{2} \left(\frac{x^2}{2}+3x\right)e^{\frac{x}{2}} dx$
　　 $\displaystyle = \left[ (x^2+2x-4)e^{\frac{x}{2}} \right]_{0}^{2}$
　　 $\displaystyle = (2^2+2\times2-4)e^{\frac{2}{2}} - (0^2+2\times0-4)e^{\frac{0}{2}}$
　　 $\displaystyle = 4(e-1)$
のように計算できる。

解説.
部分積分は積の導関数の公式の $(fg)'=f'g+fg'$ の両辺を積分することで、 $fg=\int f'g dx + \int fg' dx$ となることと比較するとイメージがつきやすいかと思います。
(多項式関数)×(指数関数)のパターンが出題されることが多い印象です。

・問題6
$xy$ 平面上の双曲線 $\displaystyle \frac{x^2}{36}-\frac{y^2}{64}=-1$ の焦点の座標を求めよ。

Answer.
双曲線の方程式 $\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$ において、 $a=6$ 、 $b=8$ としたのがここで与えられている方程式である。
よって焦点の座標は $\displaystyle (0, \pm\sqrt{6^2+8^2}) = (0, \pm 10)$ となる。

解説.
楕円の方程式 $\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ や双曲線の方程式 $\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=\pm1$ は抑えておくと良いかと思います。

・問題7
次の極限の値を求めよ。
$\displaystyle \lim_{x \to 1} \frac{x^2+2x-3}{x^{1/3}-1}$

Answer.
$x \to 1$ の際に、 $x^2+2x-3 \to 0$ 、 $x^{1/3}-1 \to 0$ であるので、 $\displaystyle \lim_{x \to 1} \frac{x^2+2x-3}{x^{1/3}-1} = \lim_{x \to 1} \frac{(x-1)(x+3)}{x^{1/3}-1}$ は $\displaystyle \frac{0}{0}$ の不定形となる。この不定形は $a^3-1=(a-1)(a^2+a+1)$ の因数分解の利用を用いることで解消できる。

よって元の数式の分子と分母にそれぞれ $\displaystyle x^{2/3}+x^{1/3}+1$ をかけて不定形を解消させる。
$\displaystyle \lim_{x \to 1} \frac{x^2+2x-3}{x^{1/3}-1}$
　　 $\displaystyle = \lim_{x \to 1} \frac{(x^2+2x-3)(x^{2/3}+x^{1/3}+1)}{(x^{1/3}-1)(x^{2/3}+x^{1/3}+1)}$
　　 $\displaystyle = \lim_{x \to 1} \frac{(x-1)(x+3)(x^{2/3}+x^{1/3}+1)}{(x^{3/3}-1)}$
　　 $\displaystyle = \lim_{x \to 1} \frac{(x-1)(x+3)(x^{2/3}+x^{1/3}+1)}{(x-1)}$
　　 $\displaystyle = \lim_{x \to 1} (x+3)(x^{2/3}+x^{1/3}+1)$
　　 $\displaystyle = (1+3)(1+1+1)$
　　 $\displaystyle = 4 \times 3$
　　 $\displaystyle = 12$

解説.
$\sqrt{x}$ などが出てくる不定形の大概はこのような計算を行うことが多いので、慣れておくと良いと思います。また、因数分解の公式はよく出てくるのでこちらも慣れておくと良いです。
（学び直しにあたっては解けなくても解答見て理解できれば十分だと思います。）

・まとめ
#1〜#3で数学検定準1級の1次試験を確認しましたが、少々計算が複雑な問題が多かった印象です。そのため必ずしも解ける必要はない一方で、計算力の強化には適した内容だったのではないかと思われました。

2021-05-28

数学検定準1級の問題の解説 #2

Math

f:id:lib-arts:20210213195311p:plain

https://www.su-gaku.net/suken/wp-content/themes/su-ken/pdf/support/past_question/2020/j1q_que_1ji.pdf

https://www.su-gaku.net/suken/wp-content/themes/su-ken/pdf/support/past_question/2020/j1q_ans_1ji.pdf

#1では問題1〜2について取り扱いました。

#2では問題3〜4について取り扱います。

以下、問題3〜4についてそれぞれ確認を行います。
・問題3
3つの単位ベクトル $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ , $\displaystyle \vec{c}$ が $\displaystyle 2\vec{a}+3\vec{b}+4\vec{c}=\vec{0}$ を満たすとき、 $\displaystyle \vec{a} \cdot \vec{c}$ を求めよ。

Answer.
$\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ , $\displaystyle \vec{c}$ が単位ベクトルであることから、 $\displaystyle |\vec{a}|^2=|\vec{b}|^2=|\vec{c}|^2=1$ を満たすことを利用する。 $\displaystyle 2\vec{a}+3\vec{b}+4\vec{c}=\vec{0}$ の両辺に対して $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ , $\displaystyle \vec{c}$ との内積を取ることで、下記の3つの式が得られる。
・ $\displaystyle 2 + 3\vec{a} \cdot \vec{b} + 4\vec{a} \cdot \vec{c} = 0$ (1)
・ $\displaystyle 2\vec{a} \cdot \vec{b} + 3 + 4\vec{b} \cdot \vec{c} = 0$ (2)
・ $\displaystyle 2\vec{a} \cdot \vec{c} + 3\vec{b} \cdot \vec{c} + 4 = 0$ (3)
上記において、(1)式と(3)式を元に $\displaystyle \vec{a} \cdot \vec{b}$ と $\displaystyle \vec{b} \cdot \vec{c}$ を $\displaystyle \vec{a} \cdot \vec{c}$ の式で表し、(2)式に代入して整理をすることで、 $\displaystyle \vec{a} \cdot \vec{c} = -\frac{11}{16}$ が得られる。

解説.
なかなか計算が複雑な問題ですが、ベクトル $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ , $\displaystyle \vec{c}$ が単位ベクトルであることを利用すると解答のように解くことができます。
計算は大変ですが、ある程度は慣れておく方が難しい書籍などを読む際にも役に立つのではと思います。

・問題4
複素数 $z=-2-i$ について下記の問いに答えよ。（ $i$ は虚数単位）
① $z$ の絶対値を求めよ
② $z$ の偏角を $\theta$ としたとき、 $\sin{4 \theta}$ を求めよ。

Answer.
① $\displaystyle \sqrt{(-2)^2+(-1)^2}=\sqrt{5}$
② ①の解答と $z$ の偏角を $\theta$ としたことより、 $\displaystyle z = \sqrt{5}(\cos{\theta}+i\sin{\theta})$ のようにできる。
　　ド・モアブルの定理より、 $\displaystyle z^4 = (-2-i)^4 = \sqrt{5}^4(\cos4{\theta}+i\sin4{\theta})$ が成立する。 $(-2-i)^4=-7+24i$ より、 $\displaystyle \sin{4 \theta}=\frac{24}{25}$ となる。

解説.
複素数に関する問題です。ド・モアブルの定理やオイラーの法則などは抑えておくと良いのではないかと思います。

・まとめ
問題3などは計算が少々複雑ですが、ある程度の計算力をつけておくと難しい書籍を読む際にも色々と役に立つので多少大変でも解けるようにしておくと良いと思います。

2021-05-27

数学検定準1級の問題の解説 #1

Math

f:id:lib-arts:20210213195311p:plain

〜

以前に数学検定の2級について取り扱いましたが、準1級の問題に関しても簡単な解説を行っておければということで確認を行います。高校の数ⅢCレベルなので、数学的な記載をある程度前提とする文献を読むにあたっての基礎になるレベルだと思います。
問題は1次試験の下記を確認します。（2次試験は論述で基本事項の取り扱いにあたっては不向きのため、1次試験の内容だけを取り扱うこととしました。）

https://www.su-gaku.net/suken/wp-content/themes/su-ken/pdf/support/past_question/2020/j1q_que_1ji.pdf

一応模範解答は下記で確認ができますが、答えだけだと理解にならないので解説も含めて行います。

https://www.su-gaku.net/suken/wp-content/themes/su-ken/pdf/support/past_question/2020/j1q_ans_1ji.pdf

以下、問題1〜2について確認を行います。
・問題1
次の不等式を解け。
$\displaystyle \log_{\frac{1}{2}} 2x$ ＞ $\displaystyle \log_{\frac{1}{2}} (x^2-2x+3)$

Answer.
$\displaystyle \log_{\frac{1}{2}} x$ は単調減少の関数であるため、不等式を満たすには $2x$ ＜ $x^2-2x+3$ が満たされれば良い。
$x^2-4x+3$ ＞ $0$
$(x-1)(x-3)$ ＞ $0$
よって上記を解いて、 $x$ ＜ $1$ , $x$ ＞ $3$ を得る。

解説.
対数関数の底が $\frac{1}{2}$ であるのでグラフは単調減少のグラフとなります。数式だけ見て考えると間違えやすいため、グラフなども同時に描きつつ考えるとミスが少なくなると思います。

・問題2
$3x+4y-20 = 0$ と $3x+4y+50 = 0$ の間の距離を求めよ。

Answer.
$\displaystyle (0, -\frac{25}{2})$ を $P$ とした時に、 $\displaystyle y = -\frac{3}{4}x+5$ への垂線の $\displaystyle y = -\frac{3}{4}x+5$ との交点を $H$ とすると、 $PH$ の長さを求めれば良い。

垂線の方程式は $\displaystyle y = \frac{4}{3}x-\frac{25}{2}$ となる。
$\displaystyle y = -\frac{3}{4}x+5$
$\displaystyle y = \frac{4}{3}x-\frac{25}{2}$
この際に上記の連立方程式を解いて $\displaystyle (x,y) = \left(\frac{42}{5},-\frac{13}{10}\right)$ を得る。求める距離は、 $\displaystyle \left(0,-\frac{25}{2}\right)$ と $\displaystyle \left(\frac{42}{5},-\frac{13}{10}\right)$ の距離であるので下記のように計算できる。
$\displaystyle \sqrt{\left(\frac{42}{5}\right)^2 + \left(-\frac{25}{2}-\left(-\frac{13}{10}\right)\right)^2}$
　　 $\displaystyle = \sqrt{\left(\frac{42}{5}\right)^2 + \left(\frac{56}{5}\right)^2}$
　　 $\displaystyle = \frac{7}{5}\sqrt{6^2 + 8^2}$
　　 $\displaystyle = \frac{7}{5} \times 10$
　　 $\displaystyle = 14$

解説.
かなり複雑な式変形となりましたが結果はシンプルな形となりました。 $3:4:5$ の直角三角形の斜辺の長さが $\displaystyle 5+\frac{25}{2} = \frac{35}{2}$ であることを利用して、これに $\displaystyle \frac{4}{5}$ をかけて、 $14$ を求めることもできます。

・まとめ
トピックというよりは計算が少し複雑な問題だったかもしれません。もちろん計算量の少ない解法は色々と探せば見つかりますが、時には計算力で解き切るようにもすると力がつきやすいかと思います。

↓以下簡単な宣伝ですが、教科書的な解説や基本的な問題演習がある方が望ましい方は下記を確認してみてください。数学検定2級〜準1級の話題を可能な限りシンプルにまとめました。

2021-05-15

TransGAN｜DeepLearningを用いた生成モデルの研究を俯瞰する #5

DeepLearning GenerativeModel Machine Learning Transformer paper

f:id:lib-arts:20210515195221p:plain

当シリーズでは生成モデルの研究や実装の俯瞰を行います。#4ではSemi-Supervised GAN(Semi-Supervised Learning with Generative Adversarial Networks)について取り扱いました。

#5では、GANにTransformerの考え方を導入した研究である、TransGAN(TransGAN: Two Transformers Can Make One Strong GAN)について取り扱います。

[2102.07074] TransGAN: Two Transformers Can Make One Strong GAN

以下目次になります。
1. TransGANの概要(Abstract、Introductionの確認)
1-1 Abstractの確認
1-2 Introductionの確認(Section1)
2. 論文の重要なポイントの抜粋
2-1. Relative Works(Section2)
2-2. Technical Approach: A Journey Towards GAN with Pure Transformers(Section3)
2-3. Comparison with State-of-the-art GANs(Section4)
2-4. Conclusions, Limitations, and Discussions(Section5)
3. まとめ

1. TransGANの概要(Abstract、Introductionの確認)
1-1 Abstractの確認
1-1節では論文のAbstractについて簡単に確認を行います。

f:id:lib-arts:20210515195403p:plain

上記がAbstractの記載ですが、要旨を下記にまとめます。

・TransformerのComputer Visionの分野への導入が取り組まれているが、GAN(generative adversarial networks)についても取り組むにあたってTransGANの研究が行われた。
・畳み込みを一切用いないで(completely free of convolutions)Transformerの処理だけに基づくarchitectureのTransGANを構築した。
・TransGANは段階的に解像度を上げる(progressively increases feature resolution)ことでmemory-friendlyなTransformer構造に基づき構築されている。

基本的には「TransformerをGANのタスクに導入した」が主題ですが、"progressively increases feature resolution"の記載は以前取り扱ったProgressive GAN(Progressive growing of gans for improved quality, stability, and variation)の研究を指していることは抑えておくと良いと思います。

Abstractについて大まかに確認できたので1-1節はここまでとし、続く1-2節では論文のSection1のIntroductionについて確認します。

1-2 Introductionの確認(Section1)
1-2節ではIntroductionをパラグラフ単位で確認を行います。

f:id:lib-arts:20210515201439p:plain

第一パラグラフでは、GANの初期研究の成功や、一貫して取り組まれてきた学習にあたっての安定化(stabilizing GAN training)の課題について紹介されています。
ここで、"Radford et al., 2015"は以前取り扱ったDCGAN(Deep Convolutional GAN)であることは抑えておくと良いと思います。

f:id:lib-arts:20210515202147p:plain

第二パラグラフでは、パフォーマンスの向上にあたって、backbone（特徴量抽出器と理解すれば良いです）に関するablation study(条件を一つずつ変えて行う実験)によりResNetやそれ以外のbackboneについて試したとされています。また、他の取り組みとして、self-attentionやstyle-based generator(StyleGAN)、自己回帰Transformerなどが挙げられています。

f:id:lib-arts:20210515203043p:plain

f:id:lib-arts:20210515203059p:plain

第三パラグラフでは、GANのbackboneを選定するにあたっての共通認識(commonsense)として、CNNの構造が基本とされていたことについて記載されています。畳み込みは強力なinductive bias(前提の構造を決めることによって学習力を高めることができるが、これをinductive biasと呼んでいる)を持つため、Computer Visionにおいては基本的に畳み込みの構造が用いられてきました。

f:id:lib-arts:20210515203911p:plain

続くパラグラフでは、畳み込みの問題点の"local receptive field"について記載されています。これによって、広い範囲の依存性(long-range dependencies)が取り扱えないとされています。これはCNNがself-attentionやnon-localな演算を用いた研究に比べ、大域的な統計量(global statistics)を取得できないという点を示唆していると考えて良いかと思います。

以下は、何箇所か抜粋して確認します。

f:id:lib-arts:20210515204638p:plain

上記はこれまで確認したCNNの問題点を解消するにあたって、pure Transformerを用いた構造をTransGANとしたとあります。

f:id:lib-arts:20210515204918p:plain

また、この研究のCotributionは上記にまとめられています。

2. 論文の重要なポイントの抜粋
2-1. Relative Works(Section2)
Generative Adversarial Networks(Section2-1)、Visual Transformer(Section2-2)、Transformer Modules for Image Generation(Section2-3)でそれぞれまとめられています。
詳しく確認すると冗長になると思われるのでここでは省略します。

2-2. Technical Approach: A Journey Towards GAN with Pure Transformers(Section3)

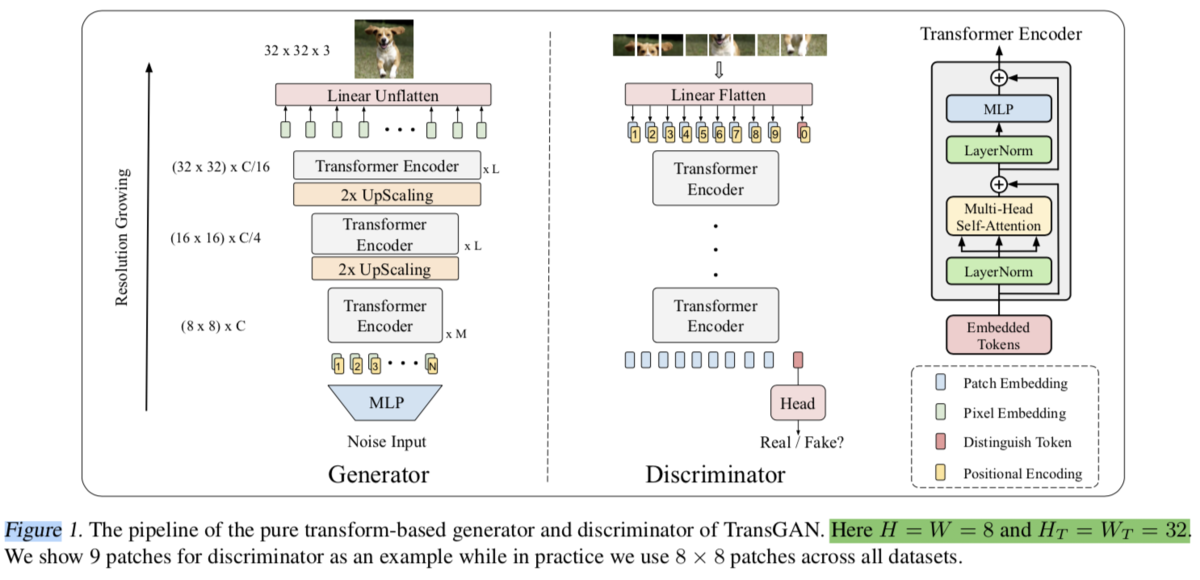
f:id:lib-arts:20210515210206p:plain

処理の全体像は上記です。Progressive GAN(Progressive growing of gans for improved quality, stability, and variation)とVisionTransformer(AN IMAGE IS WORTH 16X16 WORDS)が把握できていれば、処理の概要が把握できるかと思います。

f:id:lib-arts:20210515211219p:plain

また、論文のFigure2ではgeneratorのlossに超解像(SuperResolution)のlossを加えたことについて記載されています。

f:id:lib-arts:20210515211241p:plain

論文のFigure3では、CNNライクなinductive biasを導入するにあたって、段階的にReceptive Fieldを増やしていくことについて表されています。これによってCNNの構造的利点を活かしつつ大域的な処理も可能となるように試みたと理解して良いと思います。（関連の記載はSection3-4のLocality-Aware Initialization for Self-Attentionで記載されています）

2-3. Comparison with State-of-the-art GANs(Section4)
2-4. Conclusions, Limitations, and Discussions(Section5)
当記事では省略します。

3. まとめ
#5ではTransGAN(TransGAN: Two Transformers Can Make One Strong GAN)について取り扱いました。
#6以降でも引き続き関連の研究について確認できればと思います。

2021-05-12

プロパガンダとメディア｜政治とプロパガンダ #2

Politics Propaganda

f:id:lib-arts:20210511215624p:plain

「政治とプロパガンダ」について取り扱うシリーズです。#1ではプロパガンダの概要や主な手法についてざっくりと確認しました。

#2ではプロパガンダとメディアについて取り扱います。基本的にはWikipediaの記載を参考に、シンプルにまとめられたらと思います(プロパガンダ - Wikipedia)。
以下、当記事の目次になります。
1. テレビ・ラジオ・新聞報道を用いたプロパガンダ
2. 映画・芸術を用いたプロパガンダ
3. 集会・イベントやインターネットを用いたプロパガンダ
4. 建国神話・英雄譚・伝説・学説の利用
5. まとめ

1. テレビ・ラジオ・新聞報道を用いたプロパガンダ
1節ではテレビ・ラジオ・新聞報道を用いたプロパガンダについて取り扱います。基本的には「マスメディアをどのようにプロパガンダに用いるか」の視点で考えておくと良さそうです。
テレビとラジオはデバイス的な意味でのメディアの進化のタイミングと世界史を関連付けるとわかりやすく、ラジオは第二次世界大戦頃のナチスドイツや大日本帝国、テレビは冷戦時のソ連で行われたプロパガンダが有名な例と考えておくのが良いと思います。

f:id:lib-arts:20210512224514p:plain

上記のように特にナチスドイツではラジオの市場価格を下げてでもラジオの普及を推奨したなどからも、いかにメディアを活用するかが重視されていることがわかります。ナチスドイツのプロパガンダやそれを主導した宣伝大臣のゲッペルスはこの辺りの世界史を考察する上で重要です。また、大日本帝国では国営の放送局しかなく、それが政府の宣伝機関として機能していたということは抑えておくと良さそうです。

f:id:lib-arts:20210512224544p:plain

上記はソ連のテレビを用いたプロパガンダですが、ラジオと異なるのは映像が主となるということです。このことにより、プロパガンダが逆効果になったソ連の例などもあります。

f:id:lib-arts:20210512225106p:plain

新聞報道や出版社に関しては、「言論統制により新聞や書籍でもプロパガンダ的手法がとられる場合がある」とされています。ここでよくありがちな主張に、「中立性を保つべきだ」というのがありますが、アメリカでは逆に新聞社の立場が「保守」と「リベラル」に分かれることが許容されるかつ当然視されていることがなかなか興味深いです。というのも、株主や広告主などの資金源や新聞社の思想背景、記者の個人的信条などが原因で「完全な中立」は難しいためです。そのため、ある程度報道や出版にあたっては立場を明示する方が逆に受け取り側が中立性を判断しやすくなるかと思われます。

1節では主にマスメディアに関連するテレビ・ラジオ・新聞報道を用いたプロパガンダについて取り扱いました。続く2節では映画・芸術を用いたプロパガンダについて取り扱います。

2. 映画・芸術を用いたプロパガンダ
2節では映画・芸術を用いたプロパガンダについて取り扱います。

f:id:lib-arts:20210512230408p:plain

映画を用いたプロパガンダは国家や軍、政治団体やその支援者などが映画を直接製作したり積極的に協力したりすることで行われます。世界史的にはレーニンの共産主義プロパガンダ映画などが有名と抑えておくのが良さそうです。

f:id:lib-arts:20210512230719p:plain

プロパガンダに芸術を用いる手法については、大日本帝国やナチス政権下のドイツが例として挙げられています。第二次世界大戦中の大日本帝国では、芸術家を国家の統制管理下におき、反体制主義の芸術家を投獄することで表現を国家統制に用いたとされています。

2節では映画・芸術を用いたプロパガンダについて取り扱いました。事実上の独裁政権の統制強化のために芸術的表現を利用するというのが主な流れのようでした。

3. 集会・イベントやインターネットを用いたプロパガンダ
3節では集会・イベントやインターネットを用いたプロパガンダについて取り扱います。

f:id:lib-arts:20210512232054p:plain

集会・イベントを用いたプロパガンダでは「会場の規模」や「装飾」などの豪華さ・贅沢さを見せつけ権威性を演出したり、貧弱のものを見せつけることで大衆の味方であるように装ったりされます。この辺りのメディアの演出は現代でも少なからず行われていると思われるため、一定程度注意が必要だと思われます。

f:id:lib-arts:20210512231512p:plain
また、上記がインターネットを用いたプロパガンダの具体例です。立場を偽り、中立を装って、多数派に見せかける工作を行うのが基本的な手法だと抑えておくのが良さそうです。また、都合の良くない発信は削除させるように圧力をかけるというのもプロパガンダの手法として用いられるようです。

4. 建国神話・英雄譚・伝説・学説の利用
4節では「建国神話・英雄譚・伝説・学説の利用」について取り扱います。

f:id:lib-arts:20210512232654p:plain

上記では「建国神話は国家の正当性を表すため、重要な位置を占める」とされています。日本では、古事記や日本書紀、神風などが大日本帝国時に用いられたとされています。またここで革命により成立した人口国家のアメリカ合衆国、ソビエト連邦、中華人民共和国、中華民国では神話を持たないとされているのもなかなか興味深いです。

5. まとめ
#2ではプロパガンダとメディアについて取り扱いました。20世紀はマスメディア中心だったプロパガンダが近年ではインターネットの普及などにより個々に向けた発信が多くなってきたことには注意が必要だと思われました。
#3では憲法改正とプロパガンダについて取り扱います。