数列と漸化式①（概要と例題解説）｜高校数学の例題解説＆基本演習 #1

f:id:lib-arts:20190914203304p:plain

以前のシリーズで機械学習のアルゴリズムであるニューラルネットワークやランダムフォレストに絡めて高校レベルの数学の様々なトピックについて取り扱いました。

関数や行列など様々なトピックを取り扱ったものの、いくつか取り扱えなかったものがあるので取り扱わなかったものを中心に再収録したいと思います。
#1では勾配降下法(Gradient Descent)との兼ね合いで取り扱いはしたものの、単体では解説を行わなかった数列と漸化式について例題の解説と簡単な問題演習を行えればと思います。
以下目次になります。
1. 数列の基本
1-1. 数列、項、一般項とは
1-2. 例題①解説
2. 漸化式と一般項
2-1. 漸化式とは
2-2. 例題②解説
3. まとめ

1. 数列の基本
1-1. 数列、項、一般項とは
1節では数列の基本について取り扱います。1-2節で例題の解説に移る前に簡単な概要を抑えます。

f:id:lib-arts:20190914203700p:plain

数列 - Wikipedia
まずは概要の把握ということでWikipediaの記述を簡単に確認します。
確認すると、数列(numerical sequence)とは、数が列になったもの(sequence of numbers)のことであるとされています。単独の数というよりはまとめて考えた際に規則性を見出すといった類の考え方になります。
ここで例として挙がっているのが『1,3,5,7, ...』や『1,2,3,4, ...』などでこれらはどちらも等差数列という考え方です。またそれぞれの数が置かれる場所のことを項(term)と呼んでおり、英語表現含めて抑えておくのが良いと思います。項には置かれる順番を表現に含めて第n項と表現することが多いです。ちなみに機械学習けいの論文ではnやNはサンプル数を表すことが多く、サンプルを数える際に第i項などと呼ぶことが多い印象です。iはプログラミングをする際もindexとして用いることからindexを指しているのではないかと思われます。高校数学ではnを用いることが多いので以下nと表記していきます。
置かれる順番について理解したので、次にそれぞれの場所における値のことを考えます。第n項の値のことを一般項(general term)と定義し、 $a_{n}$ のように定義します。一般項と聞くと難しそうに聞こえますが、関数のxに対する $f(x)$ のようなものと考えておくと良いです。
$a_{n}=2n-1$
$a_{n}=n$
言葉だけ聞くとわかりにくいので上記に『1,3,5,7, ...』や『1,2,3,4, ...』の一般項について式として記しました。詳しくは後ほど解説するとして、一般項はnの式で表されることが多いということだけ一旦抑えておいてください。

1-2. 例題①解説
1-2では数列の例題について取り扱います。

ex.01
1) 以下のそれぞれの数列の一般項を求めよ
(1-A) ${2, 5, 8, 11, 14, 17, ...}$
(1-B) ${4, 6, 8, 10, 12, ...}$
(1-C) ${2, 4, 8, 16, 32, ...}$
(1-D) ${6, 12, 24, 48, 96, ...}$

2) 以下の一般項の項を列記せよ
(2-A) $a_{n}=4n-2$
(2-B) $a_{n}=3^n$

Answer.
(1-A) $a_{n}=3n-1$
(1-B) $a_{n}=2n+2$
(1-C) $a_{n}=2^n$
(1-D) $a_{n}=3×2^n$

(2-A) ${2, 6, 10, 14, 18, 22, ...}$
(2-B) ${3, 9, 27, 81, ...}$

解説.
例題とAnswerを見比べることで、一般項 $a_{n}$ と数の並びの対応について理解できるかと思います。一般項は数の並びの法則性に基づいて、第n項の値をnの式で表しています。
ここで、それぞれの法則性についてですが、(1-A)、(1-B)、(2-A)については値の増加が一定であるため等差数列(arithmetic sequence)、(1-C),
(1-D)、(2-B)は値の増加にあたって同じ数を毎回掛け合わされるので等比数列(geometric sequence)と呼んでいます。
これらの二つの数列の考え方はどちらもよく出てくるので、例題と解答を見比べながらイメージをつかんでいただけたらと思います。

2. 漸化式と一般項
2-1. 漸化式とは
2節では漸化式について取り扱います。2-1節では2-2節の例題の解説に移る前に簡単な概要を抑えます。

f:id:lib-arts:20190914213446p:plain
漸化式 - Wikipedia
まずは概要の把握ということでWikipediaの記述を簡単に確認します。
漸化式(recurrence relatin)は、各項をそれ以前の項の函数として定めるということを意味するとされています。これは再帰的に演算を定めることであり、英語表記ではrecurrenceが用いられています。
漸化式を用いた数式の定義で有名なのがフィボナッチ数列で、フィボナッチ数列は下記のような漸化式で数列を定めます。
$a_{n+2}=a_{n+1}+a_{n}$ 、 $a_{1}=1$ 、 $a_{2}=1$
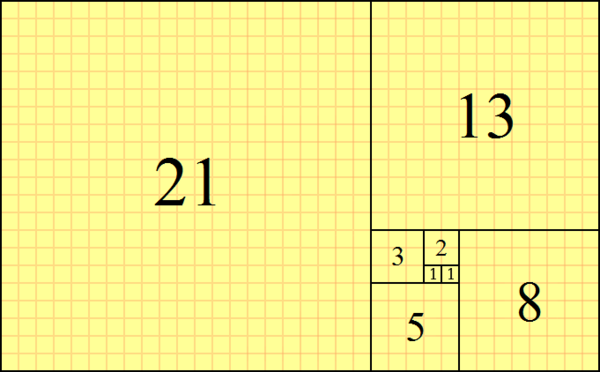
この数を並べると、 ${1,1,2,3,5,8,13,21,34,...}$ のようになります。フィボナッチ数列は冒頭の画像でも用いていますが、漸化式を用いて定義する数列においては有名な数列です。
だいたいのイメージがつかめたので、漸化式について再度まとめると、隣接する項の関係性を記述することで数の並びの規則を記述する式であるということです。また、隣接2項間の漸化式なら第1項、隣接3項間の漸化式なら第1項と第2項の値が定義上必要になることに注意が必要です。