確率分布のグラフ化&掛け算と対数|高校数学の演習を通して理解する確率分布と最尤法 #2

以前のシリーズで機械学習のアルゴリズムであるニューラルネットワークやランダムフォレストに絡めて高校レベルの数学の様々なトピックについて取り扱いました。
上記ではニューラルネットワークやランダムフォレストを中心に取り扱いましたが、今回は確率分布と最尤法について取り扱っていきます。
#1では集合・確率と様々な関数(指数関数、対数関数)について取り扱いました。
集合・確率&様々な関数(指数関数、対数関数)|高校数学の演習を通して理解する確率分布と最尤法 #1 - lib-arts’s diary
#2では確率分布のグラフ化と、掛け算と対数について取り扱います。
以下、目次になります。
1. 例題③ 確率分布のグラフ化
2. 例題④ 掛け算と対数
3. まとめ
1. 例題③ 確率分布のグラフ化
1節では確率分布の関数の形について見るにあたって、関数の形のグラフ化を行なってみます。
ex.03
下記の関数をPythonを用いてグラフ化せよ。
1)
2)
3)
Answer.
1)
下記コードで実装できる。
import numpy as np
import matplotlib.pyplot as pltx = np.arange(-3,3,0.1)
y = np.exp(-x**2)plt.plot(x,y)
plt.show()
実行結果は下記のようになる。
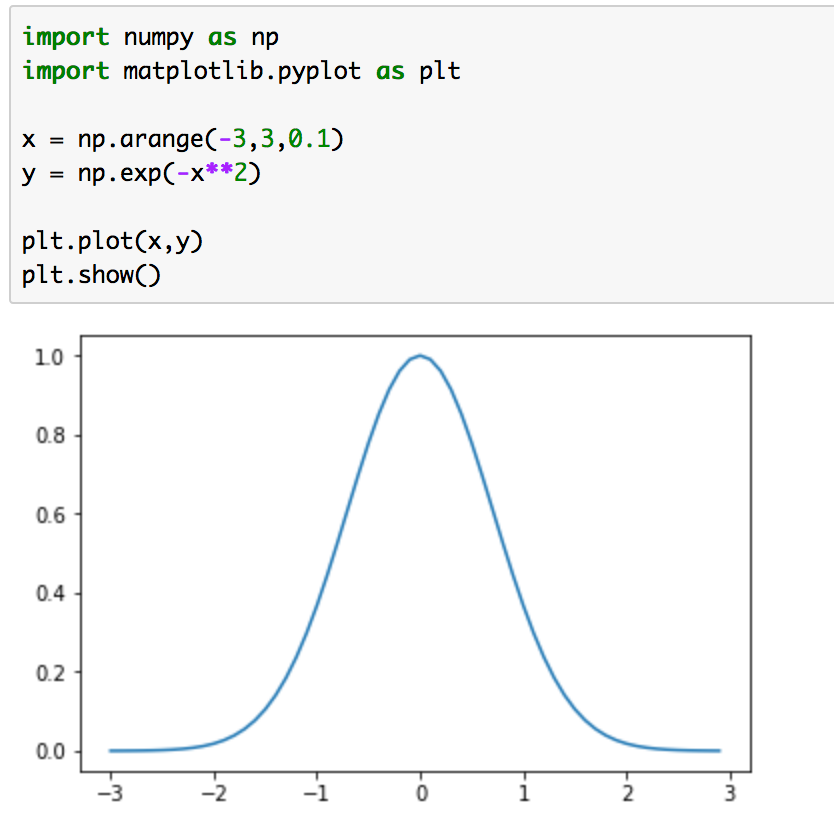
2)
下記コードで実装できる。
import numpy as np
import matplotlib.pyplot as pltx = np.arange(-3,3,0.1)
y = np.exp(-x**2/2)/np.sqrt(2*np.pi)plt.plot(x,y)
plt.show()
実行結果は下記のようになる。
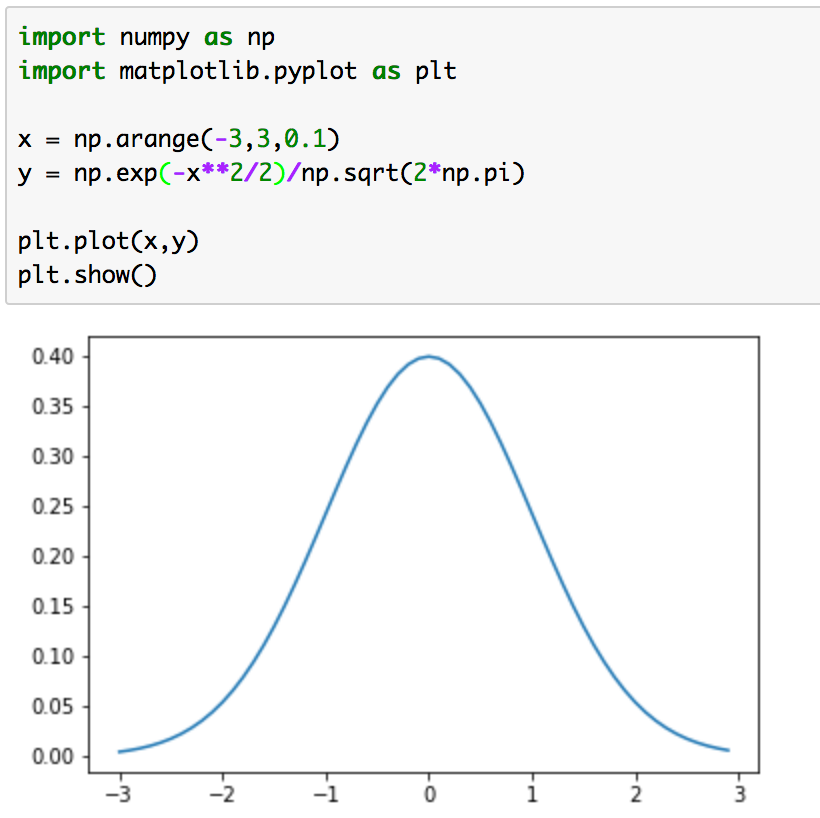
3)
下記コードで実装できる。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-2,8,0.1)
y = np.exp(-(x-3)**2/(2*4))/np.sqrt(2*np.pi*4)
plt.plot(x,y)
plt.show()
実行結果は下記のようになる。

解説.
1)〜3)のどの関数も、正規分布をベースに作成しています。1)は大きさの調整を行っておらず、積分した値が1にならないので確率分布ではないということに注意です。2)と3)はどちらも正規分布が元になっていますが、2)は平均が0、分散が1の正規分布、3)は平均が3、分散がの正規分布を描画しています。
2. 例題④ 掛け算と対数
2節では最尤法の際に考えることの多い、対数尤度の理解につながるように掛け算と対数の話を取り扱います。#1の例題②で見たように、対数関数は単調増加関数のため、最大値問題を解くにあたっての最大値を取る
と、
を最大にする
は一致します。したがって関数の最大値問題を考えるにあたって、対数関数を用いることがしばしばあります。
ex.04
下記の値を足し算の形に分解せよ。ただしは
であるとする。
1)
2)
3)
Answer.
1)
2)
3)
解説.
今回見たように、対数関数を用いることで掛け算(積)の分解を行うことができます。最尤法では同時確率(joint probability)を尤度とみなすにあたって、サンプルの生成に独立性を仮定すると尤度は掛け算の式になります。この時、例題の2)や3)のように式が掛け算の形で与えられるのですが、最大値・最小値問題を解くにあたっては微分を用いることが多く、微分は掛け算よりも足し算の式の方がシンプルに計算ができるため、対数関数を用いて式の形を変更することで尤度の計算を簡略化することができます。
詳しくは例題の後の記事でまとめますが、今回の2)と3)の例題の変形は意識して把握しておいていただけると良いかと思います。
3. まとめ
#2では確率関数のグラフ化と、掛け算と対数について取り扱いました。
#3では合成関数の微分と最大値問題について取り扱います。