変分推論の枠組みにおけるEMアルゴリズム｜Python実装で理解する変分推論(VariationalInference) #3

f:id:lib-arts:20201022172002p:plain

当シリーズはPython実装を通して変分推論を理解していこうということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

#1、#2ではKLダイバージェンスやイェンセンの不等式について確認を行いました。

#3では変分推論の枠組みにおけるEMアルゴリズムを混合正規分布(Gaussian Mixture Models)を題材にしながら確認していきます。主にBishop[2006]のSection9.2〜10.1の内容を参照します。
以下、目次になります。
1. 基礎的な理論の確認(変分推論とEMアルゴリズム)
2. 混合正規分布とEMアルゴリズム
3. まとめ

1. 基礎的な理論の確認(変分推論とEMアルゴリズム)
1節では変分推論とEMアルゴリズムに関する基本的な理論について確認します。

f:id:lib-arts:20201023173537p:plain

変分推論を考えるにあたってまず抑えておきたいのが上記の数式です。(9.70)式における $\ln p(\mathbf{X} | \mathbf{\theta})$ は対数尤度を表しており、通常の最尤推定(MLE; Maxmum Likelihood Estimation)は対数尤度をパラメータ $\mathbf{\theta}$ に対して最大化します。ここでは通常の最適化問題とは異なり、潜在変数(latent variables)の $\mathbf{Z}$ に対して確率分布の $q(\mathbf{Z})$ を導入することで、 $L(q,\mathbf{\theta})$ と $KL(q||p)$ の和の形に対数尤度を変形しています。 $L(q,\mathbf{\theta})$ と $KL(q||p)$ についてはそれぞれ(9.71)と(9.72)のように表現されています。（(9.70)の導出については基本的に前後の記載をそのまま用いているのでここでは省略します）

さて、ここで $L(q,\mathbf{\theta})$ を考えるにあたって注意しておくと良いのが、 $L(q,\mathbf{\theta})$ はパラメータ $\mathbf{\theta}$ に関する関数であるのと同時に、確率分布 $q(\mathbf{Z})$ に関する汎関数(functional)であるということです。汎関数は以前の記事でも述べましたが、関数を入力として値を返す関数です。（この時点で何かしらの変分法的な取り扱いが行われることがわかります。）

f:id:lib-arts:20201023175744p:plain

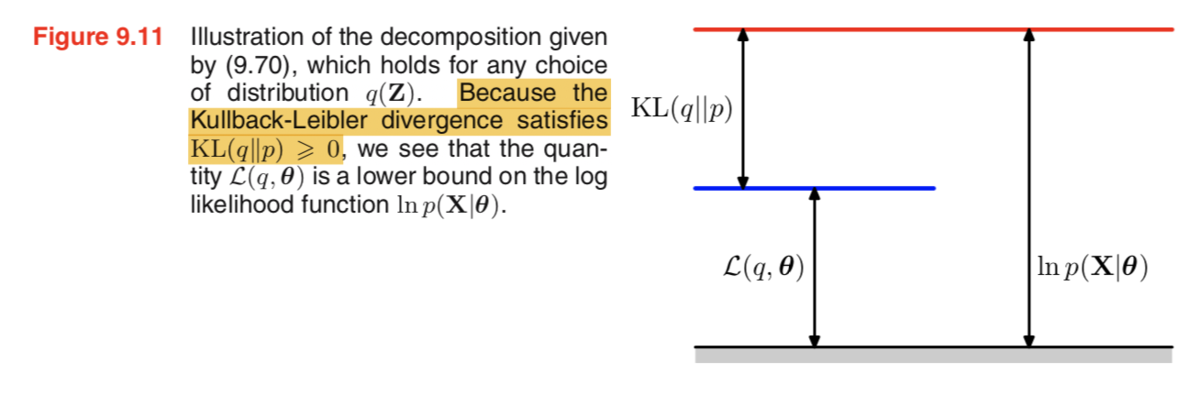
(9.70)式を図的なイメージで表すと上記のようになります。これは化学式などでエネルギーを考慮する際に用いる図と基本的には同じです。

f:id:lib-arts:20201023180652p:plain

f:id:lib-arts:20201023180712p:plain

EMアルゴリズムにおけるEステップの解釈は上記になります。パラメータの $\mathbf{\theta}$ (混合正規分布だと、各正規分布の平均や分散に相当)を固定した上で $q(\mathbf{Z})$ に対して $L(q,\mathbf{\theta}^{old})$ を最大化します。より具体的には $\mathbf{\theta}$ を $\mathbf{\theta}^{old}$ に固定した状況におけるKLダイバージェンスを0にします。KLダイバージェンスを0にするにあたっては $\ln$ の中を全ての要素に対して1にする必要があるので、 $q(\mathbf{Z})$ と $q(\mathbf{Z}|\mathbf{X},\mathbf{\theta}^{old})$ を一致させる必要があります。こうすることでFigure9.12の青矢印のように固定した $\mathbf{\theta}^{old}$ に関してlower boundを最大化させることができます。

f:id:lib-arts:20201023182412p:plain

f:id:lib-arts:20201023182639p:plain

一方Mステップの解釈は上記とされています。

f:id:lib-arts:20201023183112p:plain

f:id:lib-arts:20201023183126p:plain

f:id:lib-arts:20201023183142p:plain

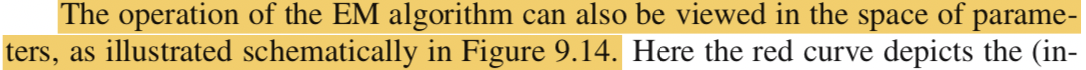
パラメータ空間におけるEMアルゴリズムの処理概要は上記とされています。Eステップでは $\mathbf{\theta}^{old}$ において赤と青の分布を一致させ、Mステップでは青の分布を最大にする $\mathbf{\theta}$ を求め、 $\mathbf{\theta}^{new}$ としています。

大体の流れがつかめたので、2節では具体的に混合正規分布をここまでの流れにあてはめて理解していきます。

2. 混合正規分布とEMアルゴリズム
2節では混合正規分布を題材にEMアルゴリズムについて確認していきます。

f:id:lib-arts:20201023200429p:plain

f:id:lib-arts:20201023200447p:plain

まず、一般的な意味合いでのEMアルゴリズムの記載は上記のようになります。Mステップにおいて(9.33)式の $Q(\mathbf{\theta},\mathbf{\theta}^{old})$ はサンプルの負担率(responsibility)を固定した上での対数尤度と同様の役割をしています。一方、Eステップでは $\mathbf{\theta}^{old}$ を固定した上で負担率(responsibility)の再計算を行っています。

f:id:lib-arts:20201023201751p:plain

f:id:lib-arts:20201023202033p:plain

また、混合正規分布におけるEMアルゴリズムは上記のようになります。Mステップは負担率を固定した上で、パラメータに尤度の最大化を行うことで導出しています。

記載だけで理解するのは大変なので、以下、実装を通してイメージを掴みます。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
%matplotlib inline

x_1 = norm.rvs(loc=0, scale=1, size=600, random_state=None)
x_2 = norm.rvs(loc=-3, scale=1, size=300, random_state=None)
x_3 = norm.rvs(loc=5, scale=2, size=100, random_state=None)
observed_x = np.r_[x_1, x_2, x_3]

plt.hist(observed_x, bins=20)
plt.show()

f:id:lib-arts:20201023221634p:plain

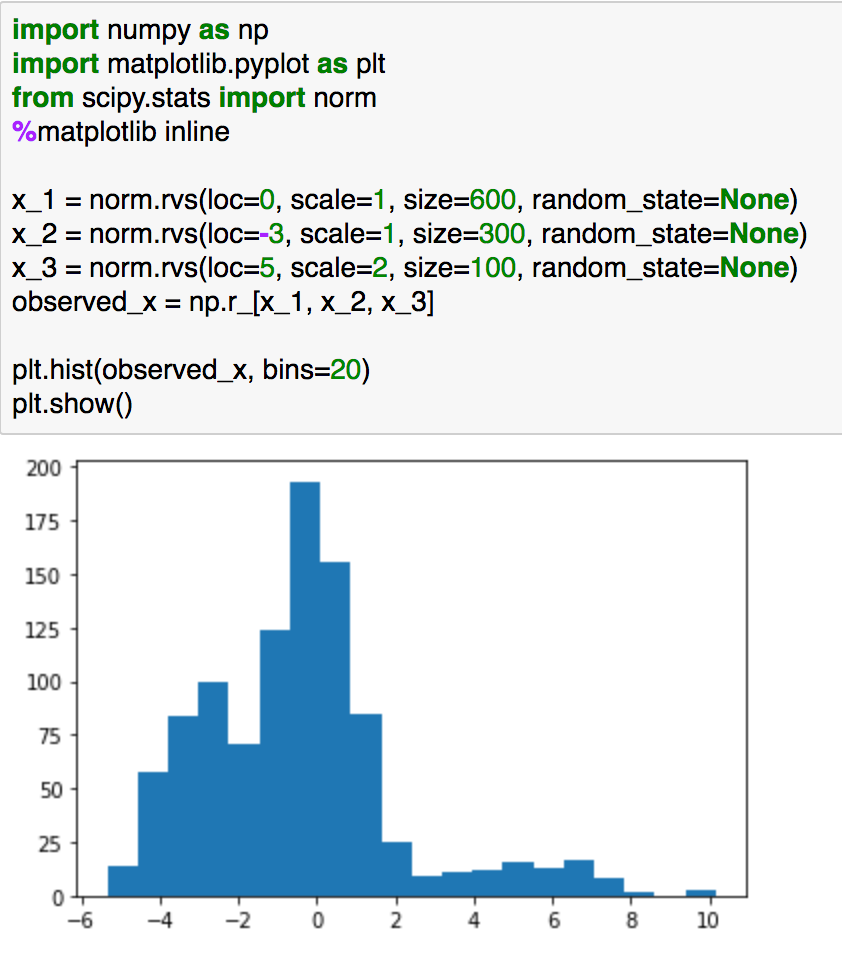
問題設定については上記のようなヒストグラムの観測が得られた際の背景にある混合分布の推定を行います。この分布は下記の混合正規分布からサンプリングしたのと同様な結果になります(累積分布関数の逆関数からサンプリングする考え方もありますが、簡易化のためこのようなサンプリングとしました)。

f:id:lib-arts:20201023222039p:plain

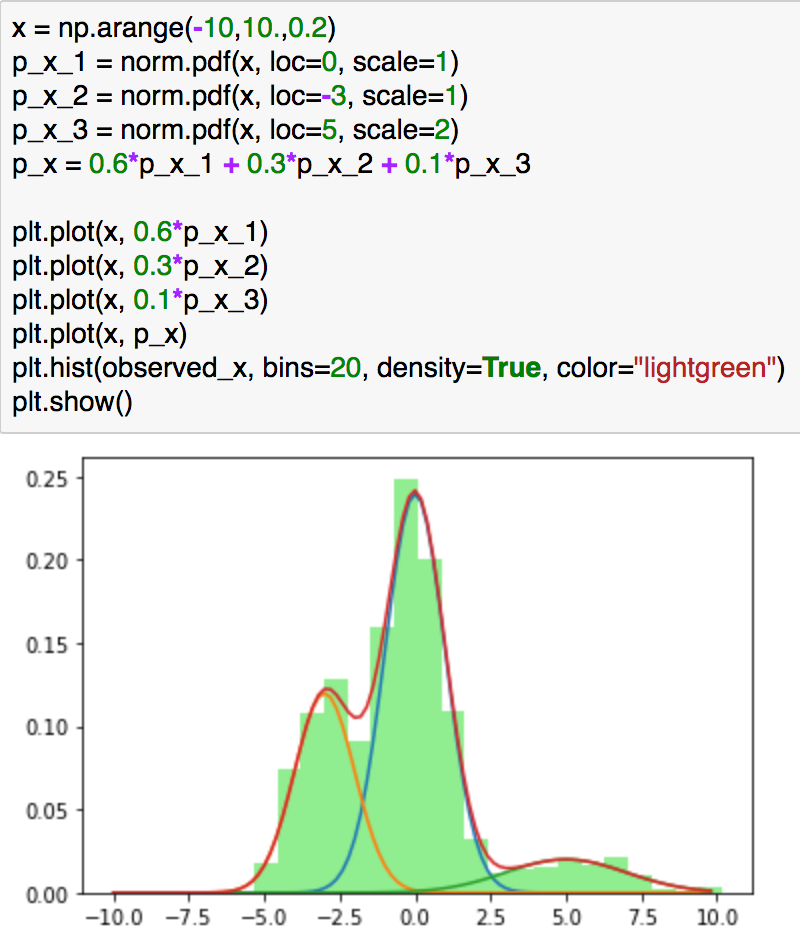
上記でイメージがつきやすいかと思います。

f:id:lib-arts:20201023222419p:plain

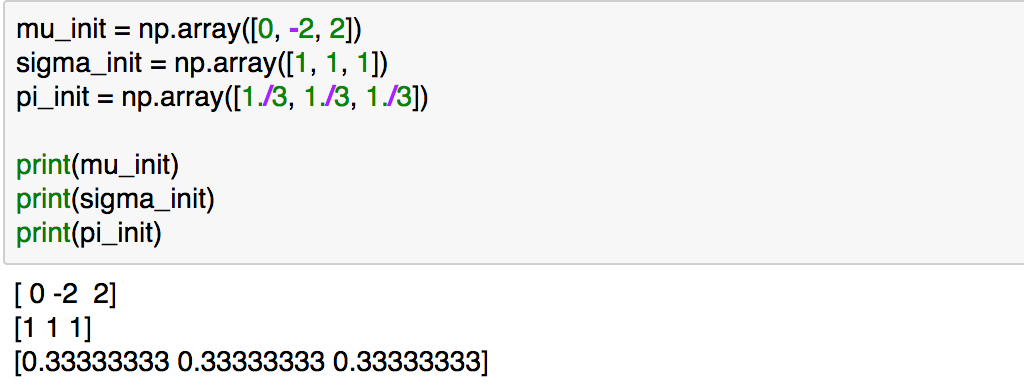
上記のように初期値を与え、下記を実行します(簡易化のため、分散は1で固定しました)。

pi = pi_init
mu = mu_init
sigma = sigma_init
gamma = np.zeros([observed_x.shape[0], 3])
for i in range(10):
# E-step
for j in range(observed_x.shape[0]):
for k in range(3):
gamma[j, k] = pi[k] * norm.pdf(observed_x[j], loc=mu[k], scale=sigma[k])
gamma[j, :] = gamma[j, :]/np.sum(gamma[j, :])
# M-step
N_k = np.zeros([3])
for k in range(3):
N_k[k] = np.sum(gamma[:, k])
pi[k] = N_k[k]/1000.
mu[k] = np.sum(gamma[:, k] * observed_x)/N_k[k]
print(N_k)
print(mu)
print("====")