イェンセンの不等式とKLダイバージェンスの非負性｜Python実装で理解する変分推論(VariationalInference) #2

f:id:lib-arts:20201022172002p:plain

当シリーズはPython実装を通して変分推論を理解していこうということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

#1では変分推論の議論の中心となってくるKLダイバージェンスについて確認しました。

#2ではKLダイバージェンスの非負性(必ず0以上になる)を考えるにあたって、イェンセンの不等式を元にした導出を追いつつ、簡単に実装でも表現してみます。
以下目次になります。
1. イェンセンの不等式
2. KLダイバージェンスの非負性の導出
3. まとめ

1. イェンセンの不等式(Jensen’s inequality)
1節ではイェンセンの不等式(Jensen’s inequality)について取り扱います。

f:id:lib-arts:20201022221318p:plain

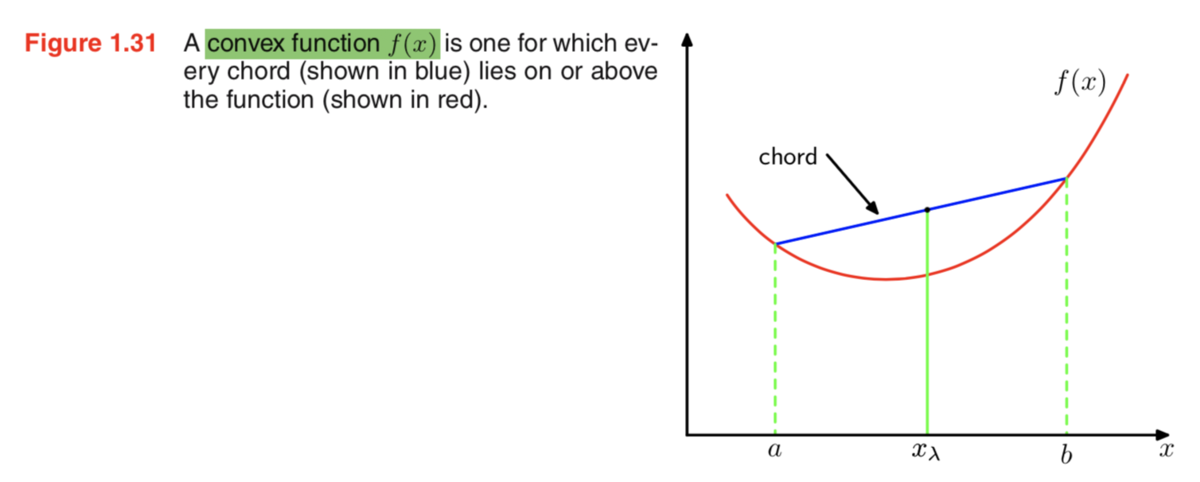
イェンセンの不等式は上記のような凸関数(convex function)とその弦(chord)について成立する不等式です。ざっくり把握するなら、弦(chord)上の点は同一のx座標における凸関数上の点よりも上に来るということです。

f:id:lib-arts:20201022221732p:plain

f:id:lib-arts:20201022221816p:plain
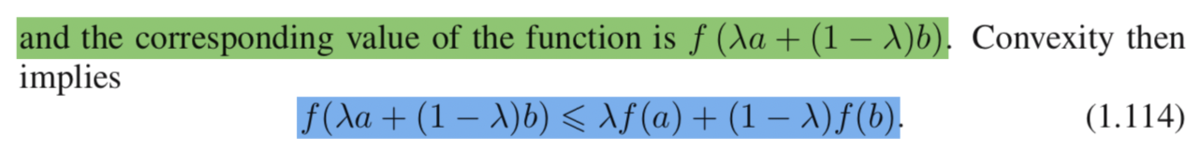
イェンセンの不等式を数式的に表すなら上記の(1.114)式のようになります。少しややこしい式ではありますが、図における $x_{\lambda}$ における弦上の点と凸関数上の点の位置関係に関する不等式となっていると解釈すれば十分です。ここで $\lambda$ は $a$ と $b$ のどちらに近いかなどを表すパラメータです。

f:id:lib-arts:20201022222407p:plain

また、イェンセンの不等式は上記のようにも考えることができます。(1.115)は3つ以上の点について取り扱うこともできるように拡張しており、(1.116)は $\lambda$ を確率分布に対応させることで期待値としてイェンセンの不等式を表しています。続く(1.117)では連続変数(continuous variable)にイェンセンの不等式を適用しています。

ここで、イェンセンの不等式の数式がややこしくなると思うのでもう一度改めて整理を行います。イェンセンの不等式を成立させるにあたって一番重要なポイントとしては、 $\displaystyle \sum_{i=1}^{M} \lambda_{i}=1$ が成立しているということです。したがって、(1.115)を考える際には $\lambda$ 、(1.116)と(1.117)を考えるにあたっては $p(x)$ が非常に重要になります。

さて、数式の議論が続きややこしくなってきたと思いますので、以下実装について見ていきます。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(-2,3,0.1)
f_x = x**2
a = [-1, 1]
b = [2, 4]
chord_x = np.arange(-1,2.1,0.1)
chord = chord_x + 2

plt.plot(x,f_x)
plt.scatter(a[0],a[1])
plt.scatter(b[0],b[1])
plt.plot(chord_x, chord)
plt.show()

まず凸関数において、上記のようにすることで問題設定を再現することができます。

f:id:lib-arts:20201022224441p:plain

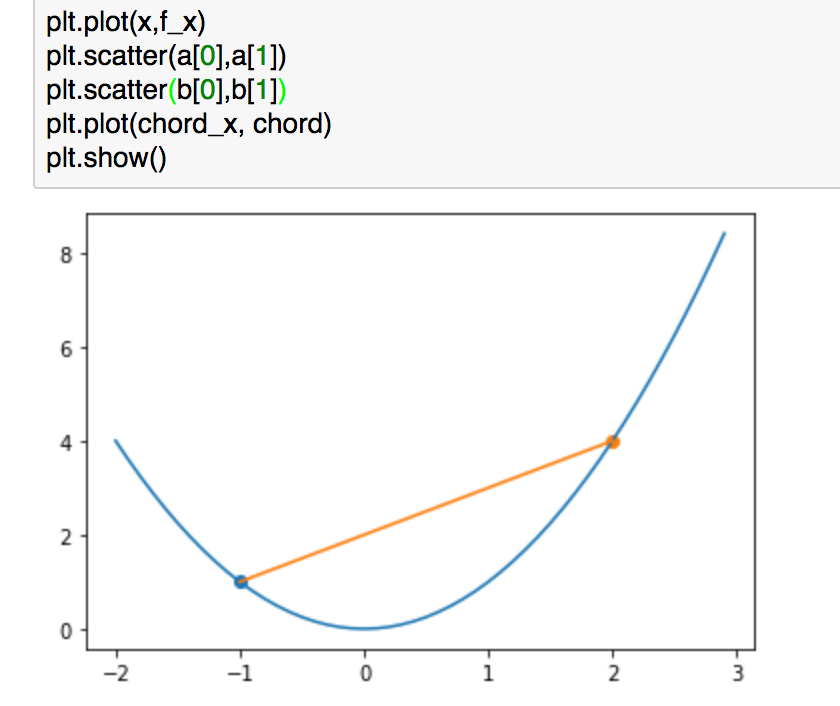
実行結果は上記のようになります。図については確認できたので、以下では具体的に $\lambda$ を用いた式を用いながら確認を行っていきます。

def calc_Jensen(a, b, f_a, f_b, lam):
chord = lam*f_a + (1-lam)*f_b
f_x = (lam*a + (1-lam)*b)**2
print("chord:{:.2f}, f_x:{:.2f}".format(chord, f_x))

calc_Jensen(-1,2,1,4,0.1)
calc_Jensen(-1,2,1,4,0.2)
calc_Jensen(-1,2,1,4,0.5)
calc_Jensen(-1,2,1,4,0.8)
calc_Jensen(-1,2,1,4,0.9)
calc_Jensen(-1,2,1,4,1.)

実行結果は下記になります。

f:id:lib-arts:20201022225624p:plain

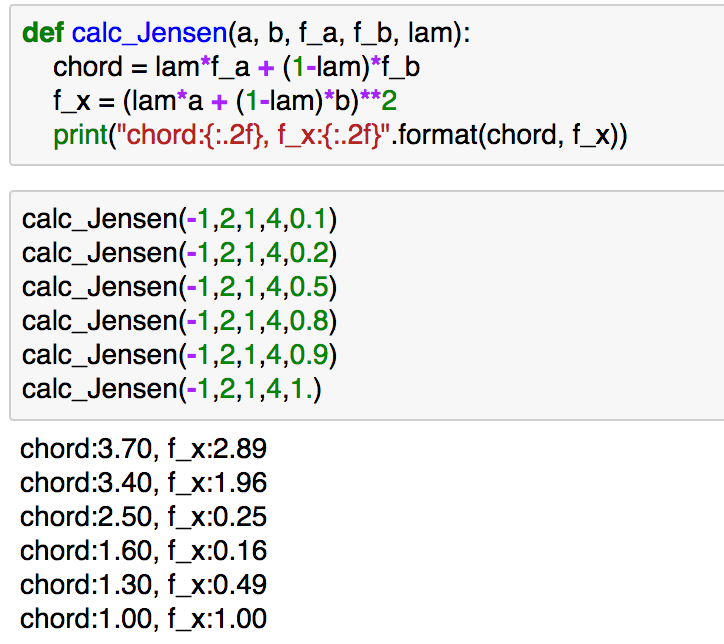
上記では様々な $\lambda$ の値に対して、イェンセンの不等式が成立しているのが確認できるかと思います。

2. KLダイバージェンスの非負性の導出
2節ではKLダイバージェンスの非負性の導出について確認します。

f:id:lib-arts:20201022230142p:plain

f:id:lib-arts:20201022230210p:plain

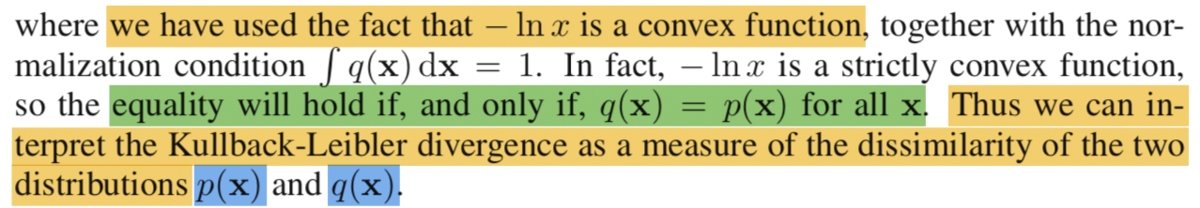
導出は上記のようになります。ここで、式(1.118)の解釈が難しいかもしれませんが、 $f(x)=-ln x$ 、 $\displaystyle g(x) = \frac{q(x)}{p(x)}$ のようにすると、積分の中の式を $-p(x)f(g(x))$ のように置き換えることができます。
$\displaystyle \int p(x) \ln \frac{p(x)}{q(x)} dx = -\int -p(x)f(g(x)) dx = \int p(x)f(g(x)) dx$
$\displaystyle \geqq f \left(\int p(x)g(x) dx \right) = -\ln \int p(x) \frac{q(x)}{p(x)} dx = -\ln \int q(x) dx = 0$
式(1.118)は確率分布の $p(x)$ と凸関数の $- \ln(x)$ に着目することで上記のような変換を行っています。ここでの式変形は混乱しやすいかもしれません。

f:id:lib-arts:20201022200517p:plain

f:id:lib-arts:20201022201547p:plain

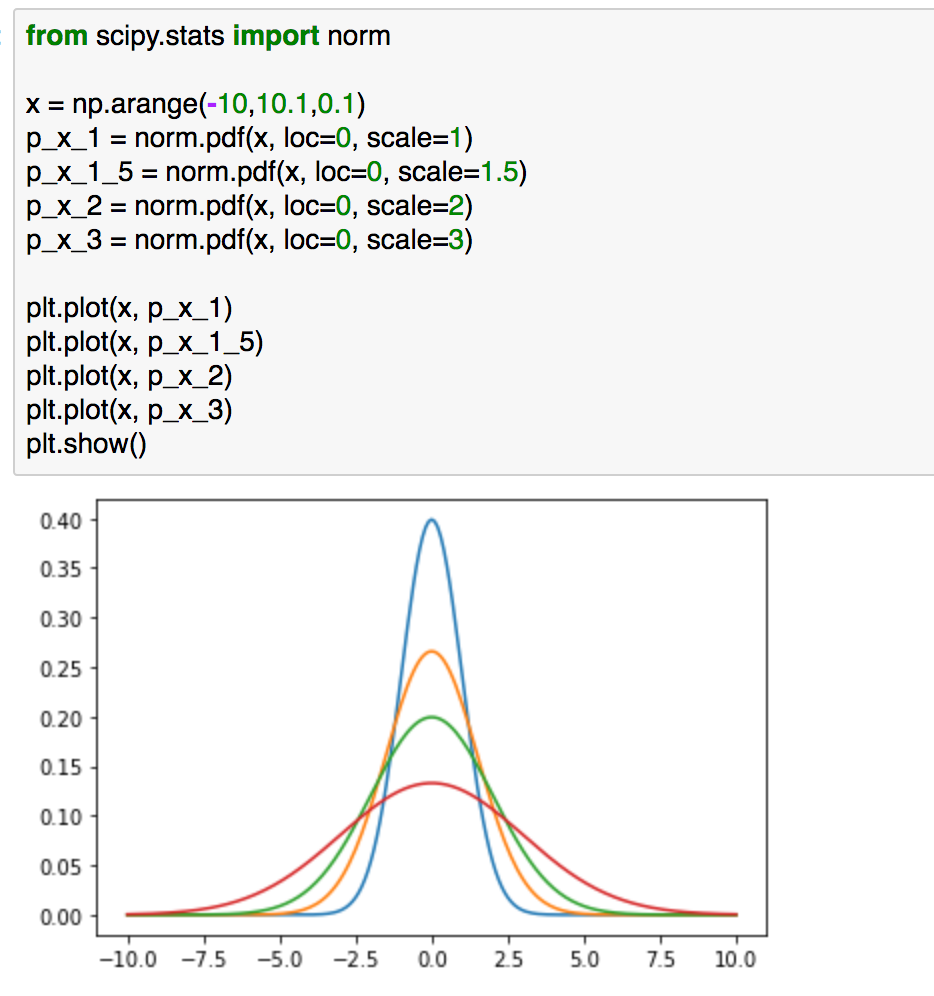
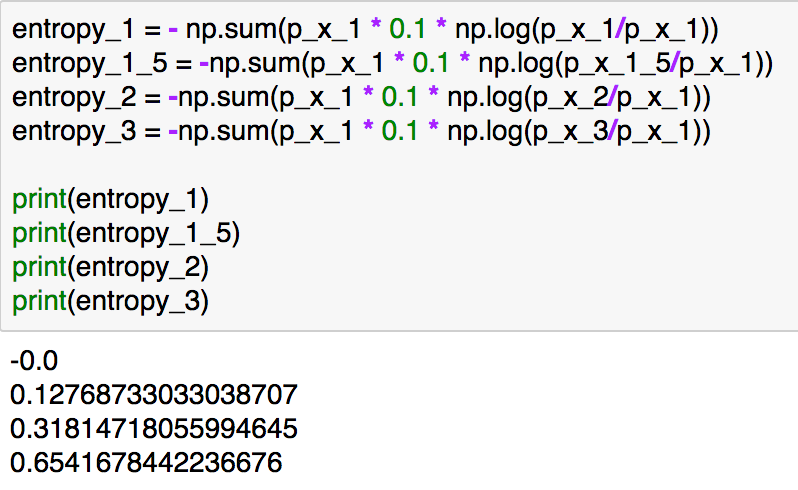
実装については#1で取り扱っているのでこちらをもう少し詳しく確認してみます。

entropy_1 = - p_x_1 * 0.1 * np.log(p_x_1/p_x_1)
entropy_1_5 = - p_x_1 * 0.1 * np.log(p_x_1_5/p_x_1)
entropy_2 = - p_x_1 * 0.1 * np.log(p_x_2/p_x_1)
entropy_3 = - p_x_1 * 0.1 * np.log(p_x_3/p_x_1)

plt.scatter(x, entropy_1)
plt.scatter(x, entropy_1_5, color="red")
plt.scatter(x, entropy_2, color="green")
plt.scatter(x, entropy_3, color="orange")
plt.show()

f:id:lib-arts:20201022234403p:plain

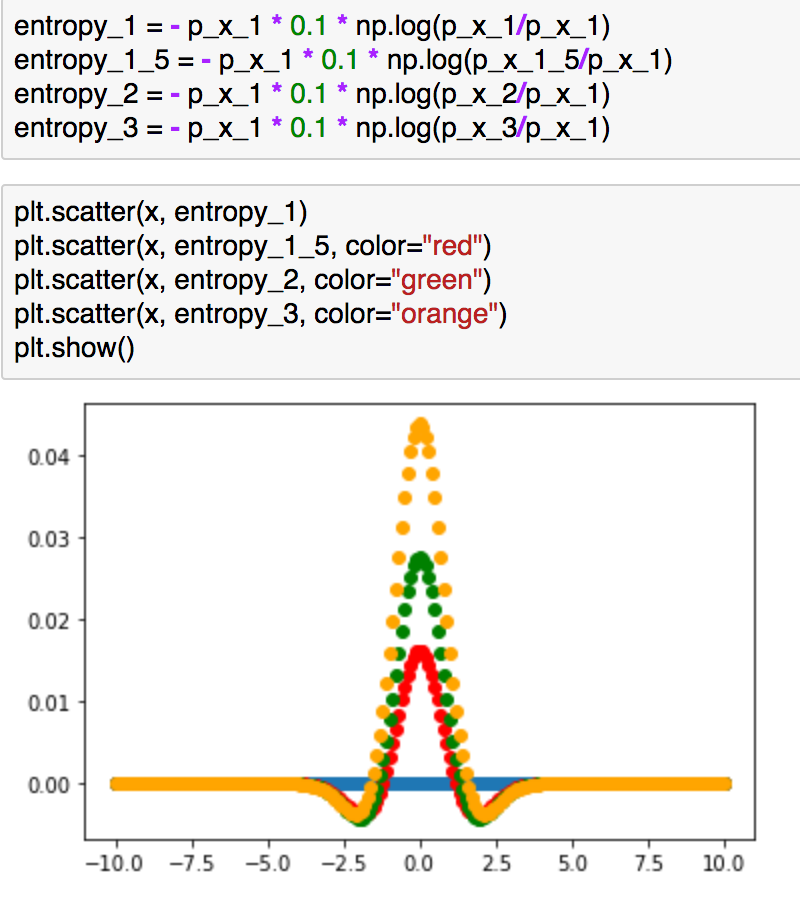
上記は、和の計算を行う前の値をプロットしたものです。分散の値の差が大きい方が(この場合のKLダイバージェンスは大きい)、0付近の値の差が大きく、これが理由でKLダイバージェンスの大きさが異なっていると考えることができるかと思います。こちらについては定性的な考察ではありますが、概要を掴むにあたっては時にはこのような考察も有意義かと思います。

3. まとめ
#2ではイェンセンの不等式とKLダイバージェンスの非負性について議論を行いました。
#3では、変分推論の文脈におけるEMアルゴリズムについて確認を行えればと思います。