Pythonを用いた誤差逆伝播(Backpropagation)の実装|微分をプログラミングする #4

当シリーズでは、近年の深層学習の発展に関連するトレンド的に微分のプログラミングの重要度は増していると思われるので、関連文脈の取りまとめを行なっています。
#1、#2、#3では自動微分の概要やSurvey論文の参照や誤差逆伝播と自動微分の関係性の確認を行いました。
#4では自動微分や誤差逆伝播を実際にPythonで実装してみます。
以下、目次になります。
1. 自動微分のPython実装
2. 誤差逆伝播のPython実装
3. まとめ
1. 自動微分のPython実装
1節では自動微分のPython実装について取り扱います。

例としては#2で取り扱った上記の「トップダウン型自動微分」について取り扱います。
import numpy as np
class GraphComputation:
def __init__(self, x1, x2):
self.v_1 = x1
self.v0 = x2
self.v1 = np.log(self.v_1)
self.v2 = self.v_1*self.v0
self.v3 = np.sin(self.v0)
self.v4 = self.v1 + self.v2
self.v5 = - self.v3 + self.v4
def calc_derivative(self):
self.rev_d_v5 = 1
self.rev_d_v4 = self.rev_d_v5*1
self.rev_d_v3 = self.rev_d_v5*(-1)
self.rev_d_v2 = self.rev_d_v4*1
self.rev_d_v1 = self.rev_d_v4*1
self.rev_d_v0 = self.rev_d_v3*np.cos(self.v0)
self.rev_d_v_1 = self.rev_d_v2*self.v0
self.rev_x2 = self.rev_d_v0 + self.rev_d_v2*self.v_1
self.rev_x1 = self.rev_d_v_1 + self.rev_d_v1/self.v_1
関連の処理を上記の計算グラフとして実装しました。クラスでの記述としたのは関数とすると返り値の受取りなどの記述が複雑になると思われたためです。これを用いて、まずはFowardの値の計算を行いますが、これは__init__で計算ができます。
func_graph = GraphComputation(2, 5)
print(func_graph.v5)
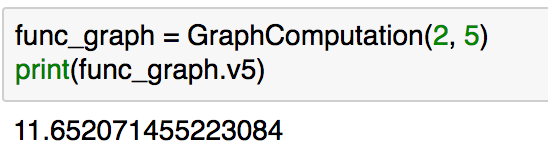
ここで得られた"func_graph.v5"は、#2で取り扱った結果と一致していることが確認できます。また、この際のと
に関する偏微分も計算してみましょう。calc_derivativeメソッドを実行することで、こちらについては結果を得ることができます。
func_graph.calc_derivative()
print(func_graph.rev_x1)
print(func_graph.rev_x2)

上記で得られた結果も#2の図に計算結果における偏微分の結果と一致していることが確認できます。
自動微分のPython実装について取り扱えたので1節はここまでとします。
2. 誤差逆伝播のPython実装
2節では誤差逆伝播のPython実装について取り扱います。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinex = np.arange(-2, 5, 0.1)
v_in = 2*x - 1
v_out = np.maximum(0, v_in)
t = 5*v_out + 1plt.scatter(x, v_in)
plt.scatter(x, v_out, color="green")
plt.scatter(x, t, color="red")
plt.show()
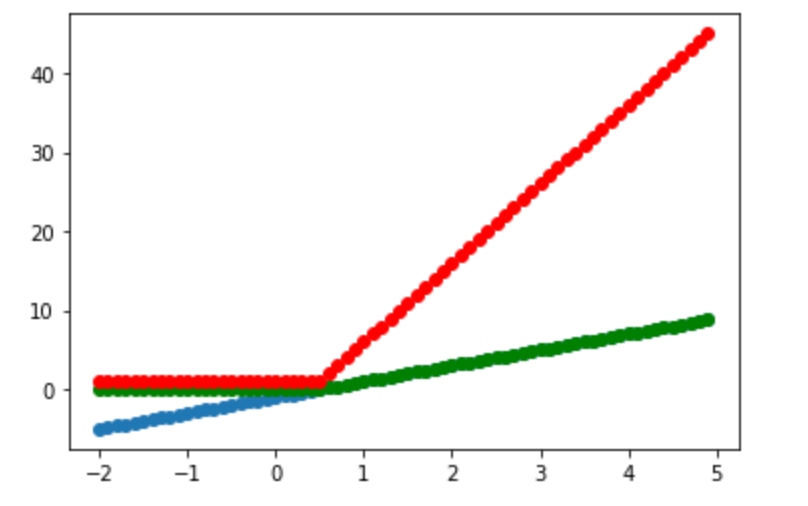
まず、問題設定ですが、上記を扱うものとします。図において、赤が予測する関数、青が活性化関数への入力、緑が活性化関数の出力を表しています。
class CalcGraph:
def __init__(self, x, t, eta):
self.x = x
self.t = t
self.eta = eta
self.w1 = 1
self.b1 = 1
self.w2 = 1
self.b2 = 1
def forward(self):
self.v_in = self.w1 * self.x + self.b1
self.relu_mask = 1.0*(self.v_in >= 0.0)
self.v_out = np.maximum(0, self.v_in)
self.y = self.w2 * self.v_out + self.b2
self.loss = np.sum((self.t-self.y)**2)
def backprop(self): self.y_grad = -2*(self.t-self.y)
self.w2 = self.w2 - self.eta*np.sum(self.y_grad*self.v_out)/self.x.shape[0]
self.b2 = self.b2 - self.eta*np.sum(self.y_grad)/self.x.shape[0]
self.w1 = self.w1 - self.eta*self.w2*np.sum(self.y_grad*self.relu_mask*self.x)/self.x.shape[0]
self.b1 = self.b1 - self.eta*self.w2*np.sum(self.y_grad*self.relu_mask)/self.x.shape[0]
これをニューラルネットワークと同様の計算とみなし、順伝播と逆伝播の実装を行うと上記になります。
eta = 0.0002
g_calc = CalcGraph(x, t, eta)
for i in range(2000):
g_calc.forward()
g_calc.backprop()
if i%500==0:
print(g_calc.loss)
print(g_calc.w1, g_calc.w2, g_calc.b1, g_calc.b2)
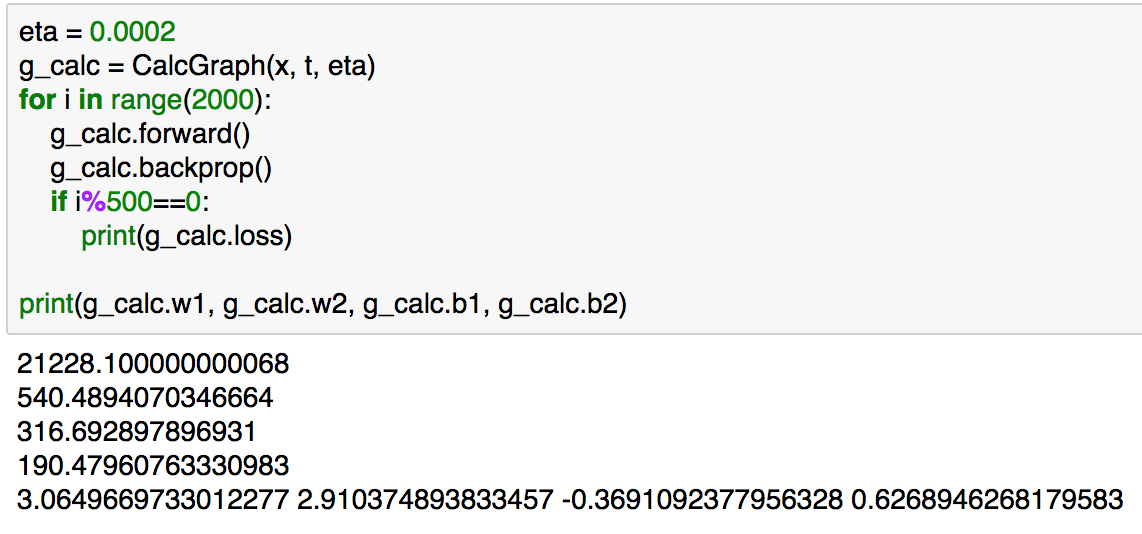
上記のように実行することで学習を行うことができます。
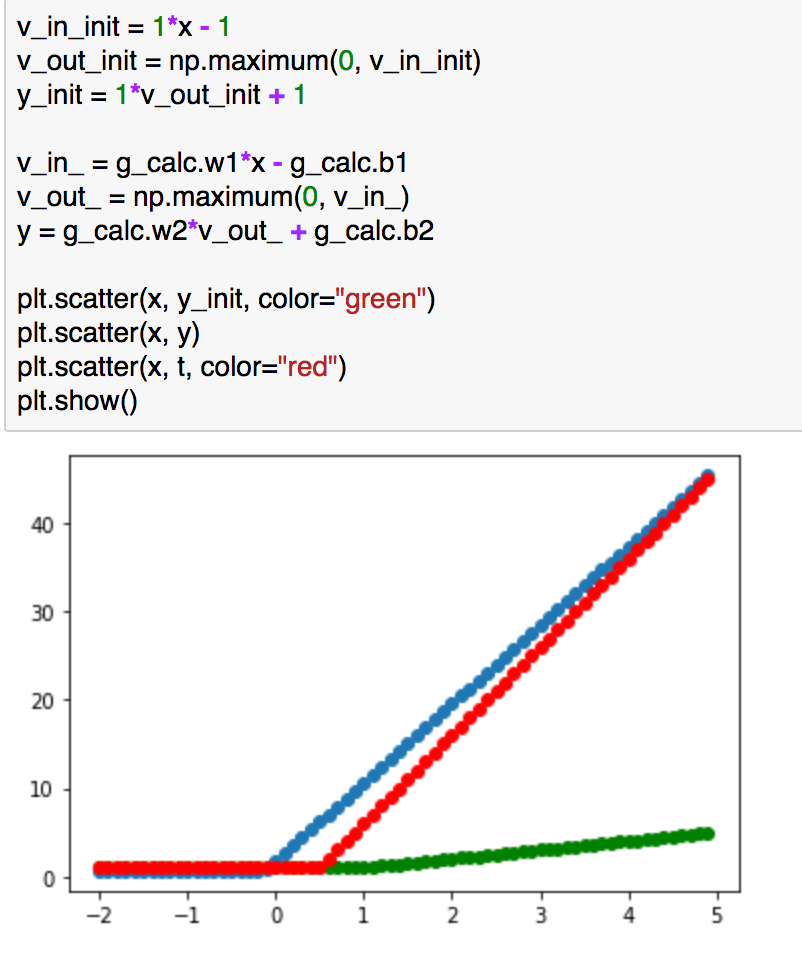
また、上記では初期値による関数(緑)、学習後(青)、実測値(緑)の比較を行っています。学習後の青が緑に近づいていることが確認できます。
3. まとめ
#4では誤差逆伝播のPython実装について取り扱いました。
#5では今回の実装を少し洗練させて多層パーセプトロン(MLP; Multi Layer Perceptron)について取り扱います。