ベクトル的取り扱いによるイェンセンの不等式の図的理解|Python実装で理解する変分推論(VariationalInference) #Appendix1

#2ではイェンセンの不等式とKLダイバージェンスの非負性について取り扱いましたが、少し考察が定性的になりましたので、もう少しイェンセンの不等式ベースでわかりやすくしようということで、Appendixを設けました。
3つ以上のや
に対する取り扱いのイメージが少々付きづらいのと、KLダイバージェンスの
の中身が
という風になっているのでややこしく見えるというのがあるためです。
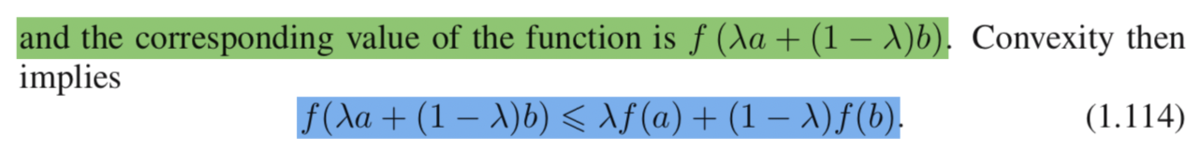

この記事では上記で表すことのできるイェンセンの不等式をベクトルの和として取り扱うことにより、より直感的な理解が可能になるようにということでまとめます。
以下、目次になります。
1. ベクトルの和と直線上の点
2. 3つ以上の点がある際のイェンセンの不等式のベクトル的取り扱い
3. まとめ
1. ベクトルの和と直線上の点
1節ではベクトルの和と直線について、数式を元に簡単に考えてみます。まず、基本的な事項として、始点(位置ベクトルなので基本的に原点で考えていればよい)を揃えた際のベクトルの和は、それぞれの係数の和が1の場合は終点を結ぶ直線上に存在します。数式で導出すると下記のようになります。
上記において位置ベクトルを持つ点Pはイェンセンの不等式(1.114)の右辺の数式に対応しており、
で位置ベクトルが表されていることからこれは線分AB(
が0以上1以下だから線分になる)上の点になります。
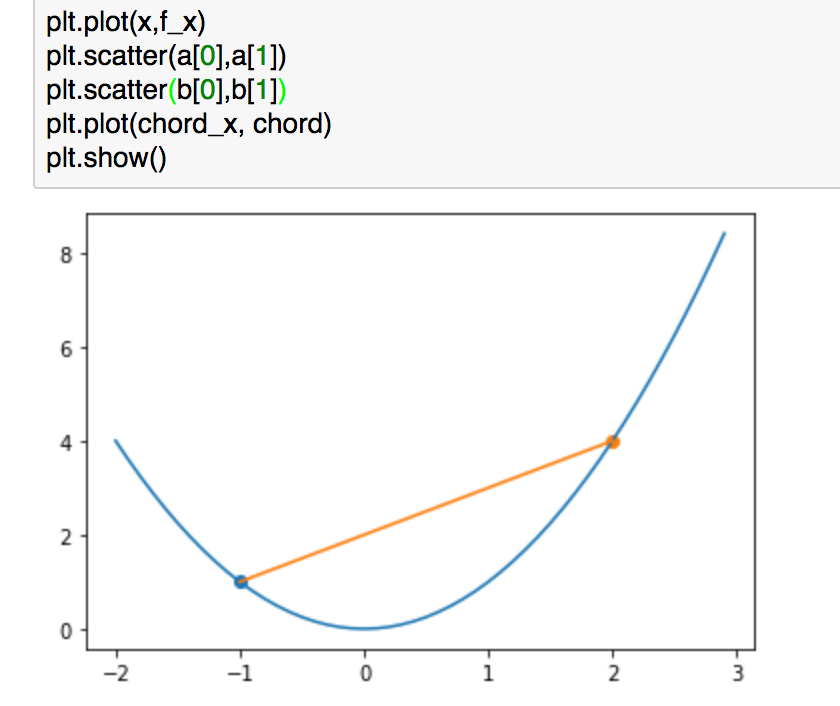
上記は#2で用いた例ですが、こちらでもう少し考えてみます。
def calc_P(lam):
OP_x = lam*a[0] + (1-lam)*b[0]
OP_y = lam*a[1] + (1-lam)*b[1]
print("P: ({:.2f}, {:.2f})".format(OP_x, OP_y))
plt.scatter(OP_x,OP_y, color="blue")
plt.scatter(OP_x,OP_x**2, color="black")plt.plot(x,f_x)
plt.scatter(a[0],a[1], color="green")
plt.scatter(b[0],b[1], color="green")
plt.plot(chord_x, chord)calc_P(0.3)
calc_P(0.5)
calc_P(0.9)
plt.plot(x,f_x)
plt.show()
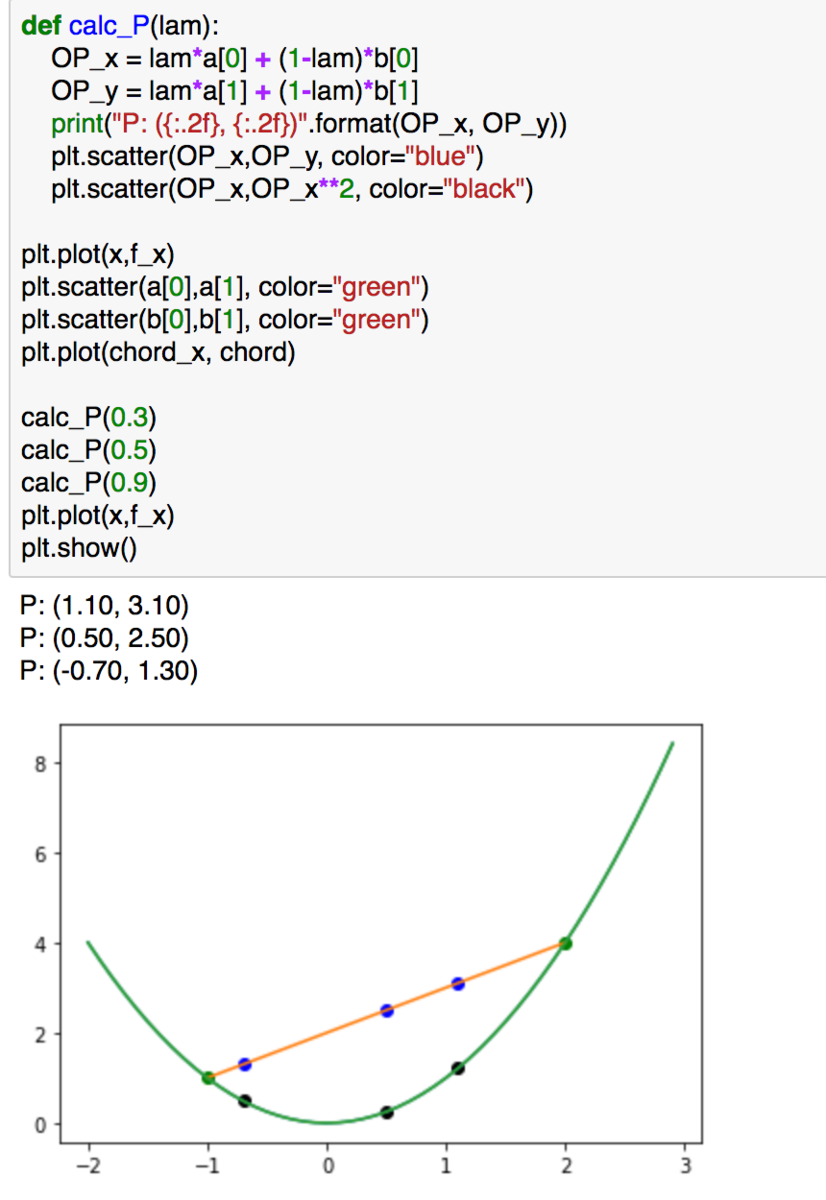
上記の青色の点に着目することで"calc_P(lam)"を用いて、線分AB上の点が表現できていることが確認できるかと思います。また、各xの値に対応する青の点と黒の点の大小関係についての不等式がイェンセンの不等式になります。
ベクトルの和とイェンセンの不等式のイメージがついたかと思いますので1節はここまでとします。
2. 3つ以上の点がある際のイェンセンの不等式のベクトル的取り扱い
1節は2点におけるイェンセンの不等式の取り扱いについて見てきました。
上記で表現できるように、イェンセンの不等式(1.114)の右側をベクトルで表すことで直線上の点であることを表現できます。
ここまでが1節の内容の確認ですが、ここでAとBだった二つの点の数を増やすとどのようになるのでしょうか。まずは3つの点で考えてみます。
数式としてはイェンセンの不等式(1.115)の右辺を元に、上記を考えていくものとします。ベクトルの和については1節と同様に考えることで下記のように計算できます。
ここで、
となるように
と
を考えると、点Pは線分
上の点となります。線分
は三角形ABCの内部に存在するため、点が2つの際と同様にイェンセンの不等式が成立することがわかります。点が3つより多い場合でも同様に議論ができるためイェンセンの不等式は成立します。
数式ばかりわかりづらいと思うので、簡単に図でも確認してみます。
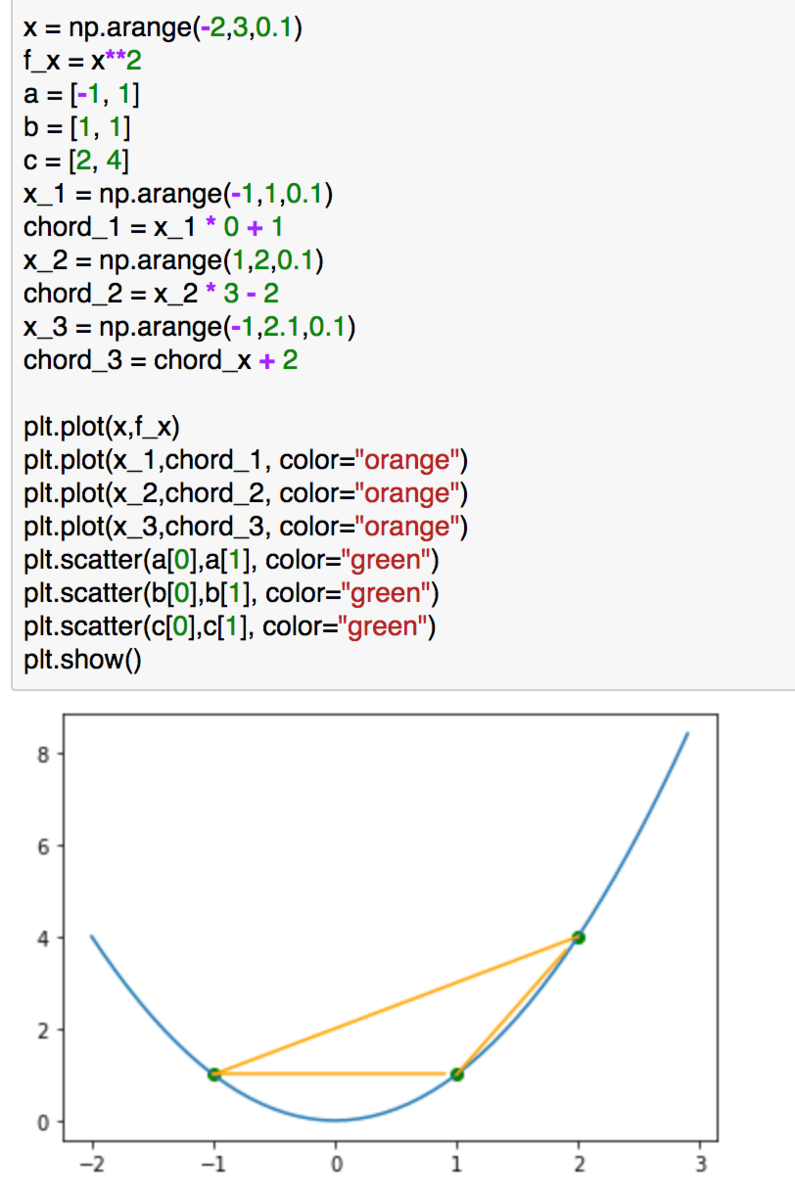
上記のような問題設定で考えるとします。関連の計算は下記によって実行できます。
def calc_P(lam1, lam2, lam3):
OP_x = lam1*a[0] + lam2*b[0] + lam3*c[0]
OP_y = lam1*a[1] + lam2*b[1] + lam3*c[1]
print("P: ({:.2f}, {:.2f})".format(OP_x, OP_y))
plt.scatter(OP_x,OP_y, color="blue")
plt.scatter(OP_x,OP_x**2, color="black")
plt.plot(x,f_x, color="dodgerblue")
plt.plot(x_1,chord_1, color="orange")
plt.plot(x_2,chord_2, color="orange")
plt.plot(x_3,chord_3, color="orange")
plt.scatter(a[0],a[1], color="green")
plt.scatter(b[0],b[1], color="green")
plt.scatter(c[0],c[1], color="green")
calc_P(0.3, 0.3, 0.4)
calc_P(0.6, 0.2, 0.2)
plt.plot(x,f_x)
plt.show()
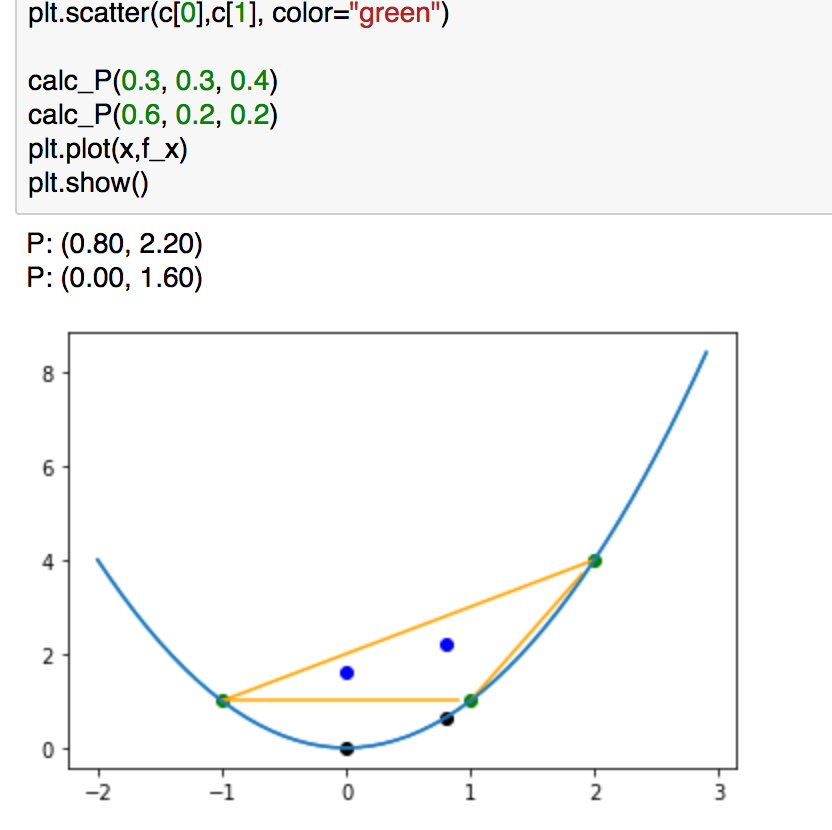
上記の青の点がオレンジの三角形の中に入っていることと、対応する黒の点よりも上にいることが確認できるかと思います。上記からイェンセンの不等式が成立している(三角形ABCは凸関数よりも上にある)ことを図的に理解できるかと思います。
3. まとめ
Appendix1ではベクトルの和について考えることで、イェンセンの不等式の図的な理解を行いました。点が3つ以上のケースが混乱しがちだと思いますが、ベクトルをベースで考えることで不等式のイメージが掴みやすくなったかと思います。