KLダイバージェンスの数式とPython実装｜Python実装で理解する変分推論(VariationalInference) #1

f:id:lib-arts:20201022172002p:plain

確率的変分推論(SVI; Stochastic Variational Inference)の論文について確認していたのですが、ベースの理解についてもう少し固める方が良さそうだったので、Python実装を通して変分推論を理解していくシリーズを新たに作成することにしました。シリーズを通してPattern Recognition and Machine Learning(Bishop, 2006)を主に参照しつつ、実装を作成します。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

#1では変分推論の議論の中心となってくるKLダイバージェンスについて確認します。Bishop[2006]のSection1-6の内容を基本的に参考にします。
以下目次になります。
1. エントロピーについて
2. KLダイバージェンスについて
3. まとめ

1. エントロピーについて
1節ではエントロピー(entropy)について確認します。

f:id:lib-arts:20201022172206p:plain

まず離散的なエントロピーですが、上記のような数式で表現されています。 $H[p]$ を解釈するにあたっては、確率分布 $p$ に対する汎関数(functional; 関数を入力とする関数)であることも把握しておくと良いです。また、基礎知識として汎関数に対する結果の最適化(最小化 or 最大化)を変分法(calculus of variations)と呼んでいることは抑えておくと良いと思います。また、エントロピーは $ln p(x_{i})$ の期待値(expectation)になっていることも抑えておくと良いと思います。

さて、数式だけで確認するとわかりづらいので、実際にPython実装を元に確認してみましょう。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(0,1,0.1)
p_x = np.tile(1.0/x.shape[0], 10)

print(x)
print(p_x)
plt.plot(x,p_x)
plt.show()

上記では1から10までにおける一様分布です。"p_x"の値が全て正かつ和が1であるので、確率分布の条件を満たしていることが確認できると思います。

f:id:lib-arts:20201022174742p:plain

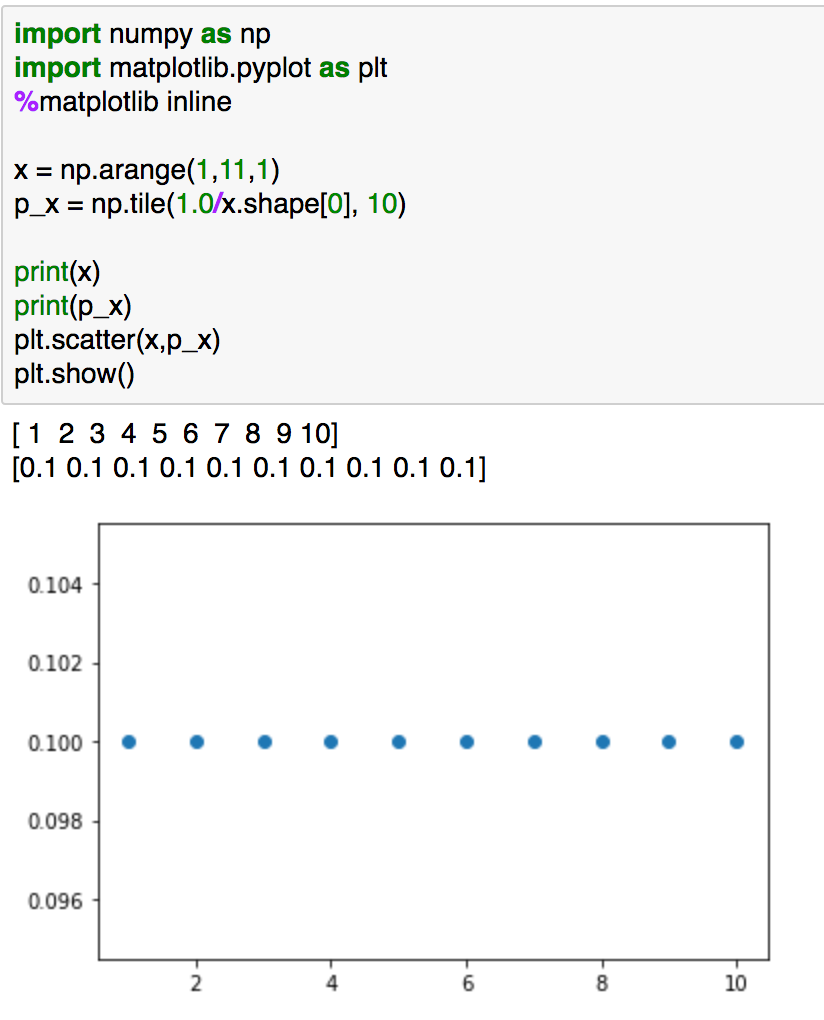
実行結果は上記になります。こちらのエントロピーについて計算します。

each_calc = p_x * np.log(p_x)

print(each_calc)
print(-np.sum(each_calc))

ここでのエントロピーの数式は $\displaystyle \sum_{i=1}^{10}x_{i} \ln p(x_{i})$ となるので、実装は"p_x * np.log(p_x)"で計算した"each_calc"の和にマイナスをつけたものになります。実行結果は下記のようになります。

f:id:lib-arts:20201022174833p:plain

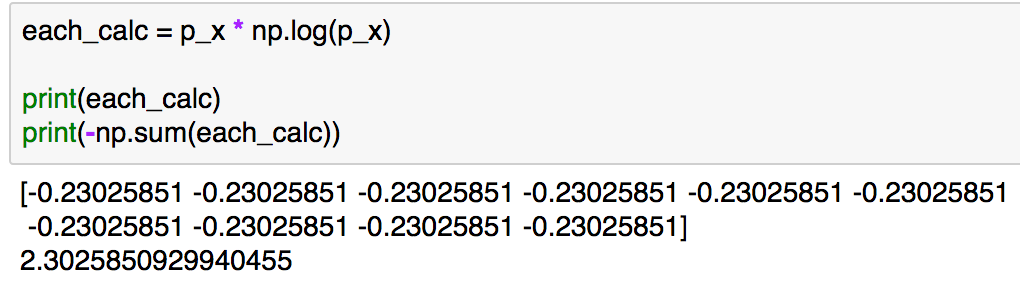
エントロピーの計算結果としては2.30...となります。

f:id:lib-arts:20201022175036p:plain

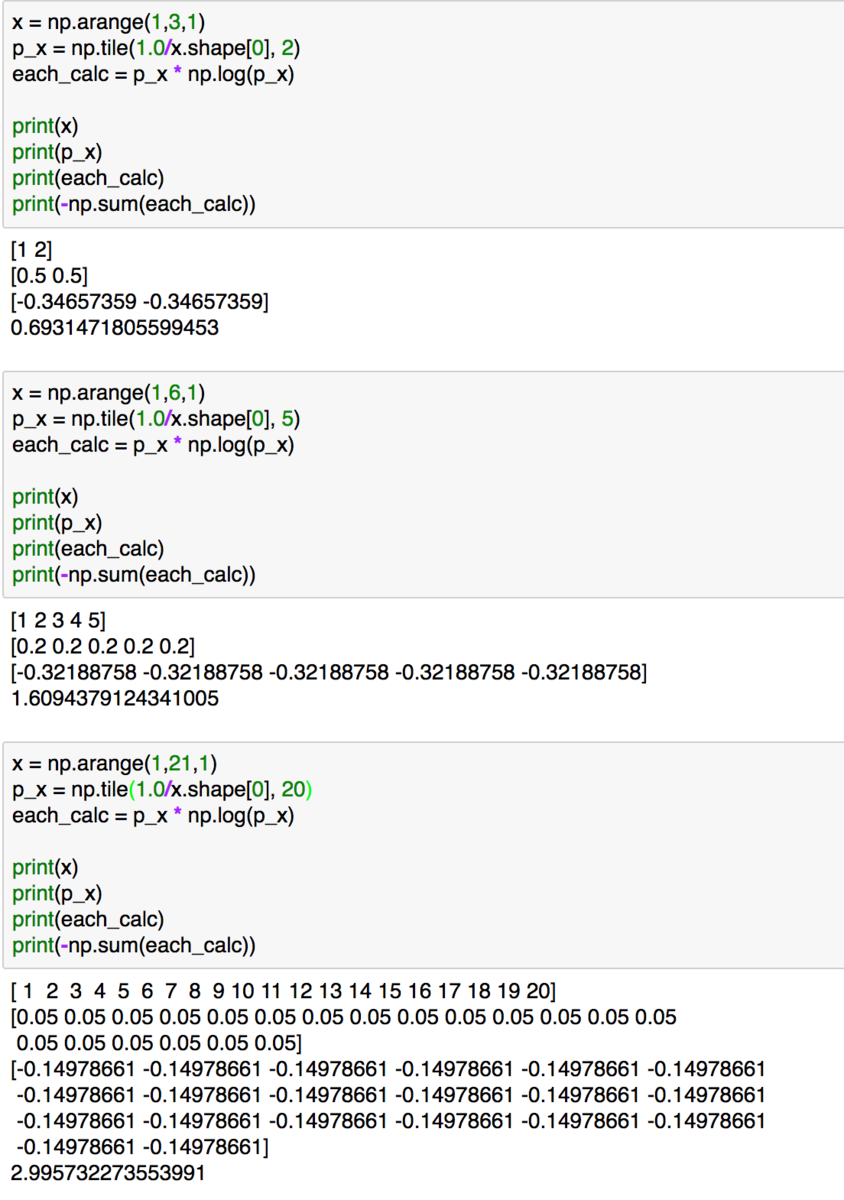
値のイメージがつきやすいように同様の計算をxの数を変えて行ってみると上記のようになります。xの数が大きくなるとエントロピーも増大していることが確認できます。

ここまでは離散的に考えていましたが、連続的にも考えてみましょう。

f:id:lib-arts:20201022184030p:plain

f:id:lib-arts:20201022184044p:plain

(1.103)の左辺の極限の中身の数式を用いて計算を行ってみます。（議論の簡易化のため、 $xlogx$ のx->+0の極限は0であることは既知とします。）

x = np.arange(0.1,10.1,0.1)
p_x = np.tile(1.0/10, 100)
each_calc = (p_x/10.) * np.log(p_x)

print(each_calc)
print(-np.sum(each_calc))

上記の実行結果は下記のようになります。

f:id:lib-arts:20201022184142p:plain

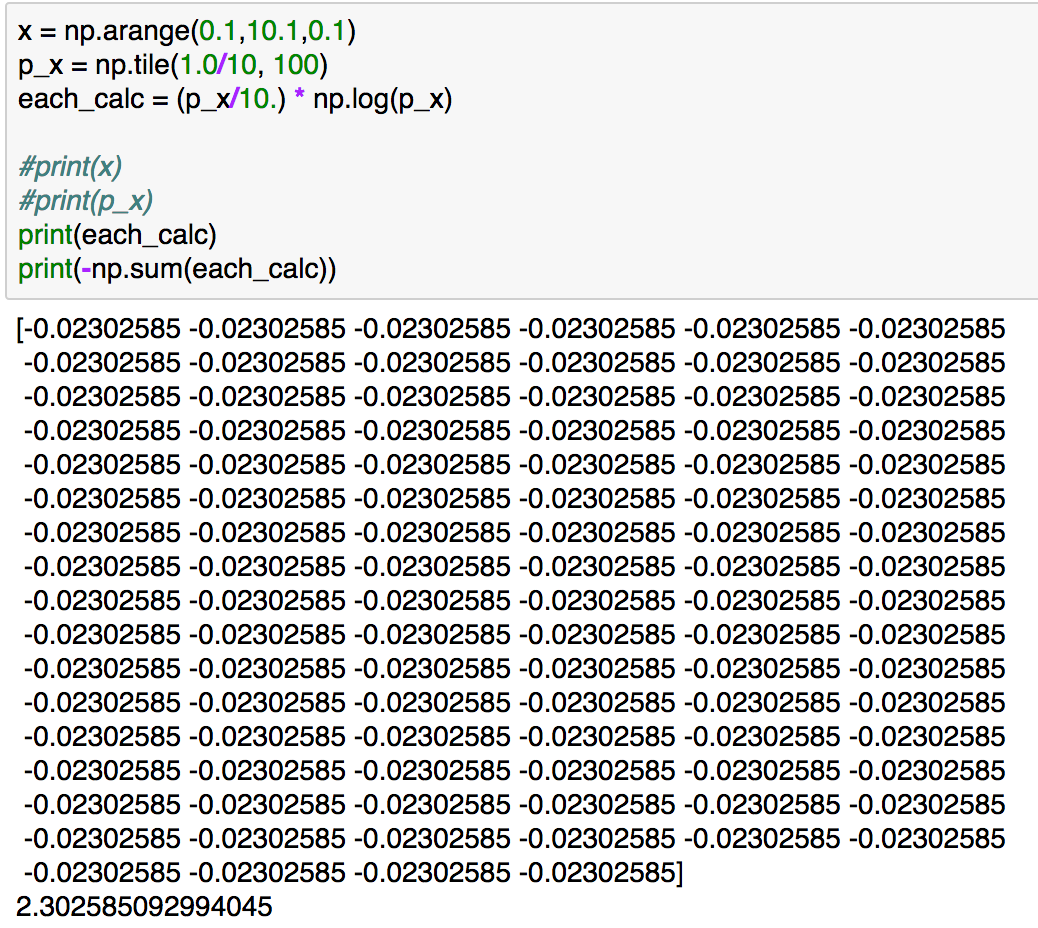
一番最初の計算例と結果が一致していることが確認できますが、同じ連続型の確率分布の区間を変えて計算を行ったと考えることもできるため、区間の取り方を変えてもエントロピーの値は基本的に変わらないというのがイメージできたかと思います。さて、(1.103)の数式ですが、区間の $\Delta$ を限りなく0に近づけることで、積分として取り扱っています。

1節では離散的な確率分布におけるエントロピーの計算における数式定義の取り扱いや、(1.103)の数式において、 $\Delta$ を0に限りなく近づけることで連続的な確率分布におけるエントロピーの計算が行えることを確認しました。2節ではこのエントロピーの数式を元にKLダイバージェンスについて確認していきます。

2. KLダイバージェンスについて
2節ではKLダイバージェンスについて確認していきます。が、1節における連続型確率分布におけるエントロピーをもう少し数式的に理解しておく方が望ましいので、先にエントロピーについてもう少し確認を行います。

f:id:lib-arts:20201022185616p:plain

まず、連続型確率分布におけるエントロピーの定義ですが、(1.104)のように行っています。ベクトル $\mathbf{x}$ について取り扱っていますが、基本的には(1.103)の式がベクトルの各要素毎に成立すると考えておけば十分だと思います。

f:id:lib-arts:20201022190026p:plain

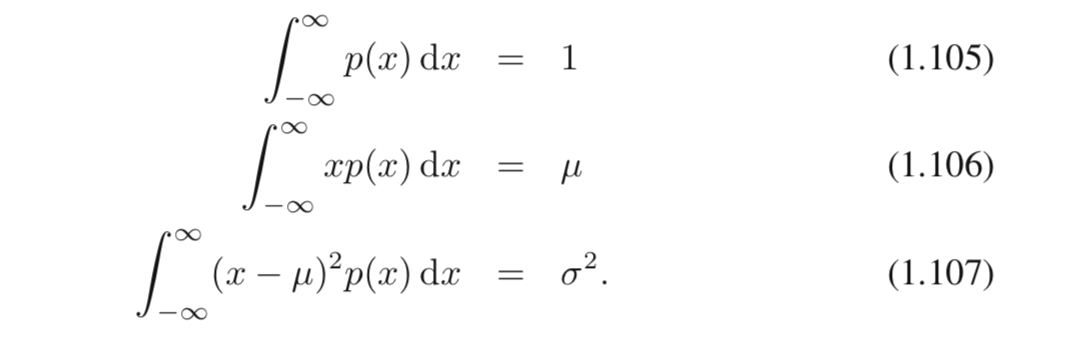
次に、エントロピーにおける三つの制約条件(constraint)について確認しますが、上記の(1.105)〜(1.107)として記載されています。(1.105)は確率分布の定義として、区間における積分が1になることを表しています。(1.106)と(1.107)は平均と分散の定義に対して、確率的な解釈を加えたものくらいに把握しておけば十分だと思います。

f:id:lib-arts:20201022190745p:plain
KLダイバージェンス(相互エントロピー; relative entropy)の記載については上記で理解しておくのが良さそうです。パターン認識(pattern recognition)の文脈でエントロピーを取り扱うにあたって、「未知の分布 $p(x)$ を近似の分布の $q(x)$ で取り扱うことを考える」というのがベースになると把握しておけば良いと思います。また、この時の指標として、(1.113)のような $KL(p||q)$ を導入したと考えれば良いと思います。KLダイバージェンスは確率分布の $p(x)$ を $q(x)$ で近似するにあたって、それぞれの類似度を計算する指標くらいに理解しておけば十分だと思います。

さて、数式だけを見ていても難しいので、実際に実装で確認してみます。

from scipy.stats import norm

x = np.arange(-10,10.1,0.1)
p_x_1 = norm.pdf(x, loc=0, scale=1)
p_x_1_5 = norm.pdf(x, loc=0, scale=1.5)
p_x_2 = norm.pdf(x, loc=0, scale=2)
p_x_3 = norm.pdf(x, loc=0, scale=3)

plt.plot(x, p_x_1)
plt.plot(x, p_x_1_5)
plt.plot(x, p_x_2)
plt.plot(x, p_x_3)
plt.show()

f:id:lib-arts:20201022200517p:plain

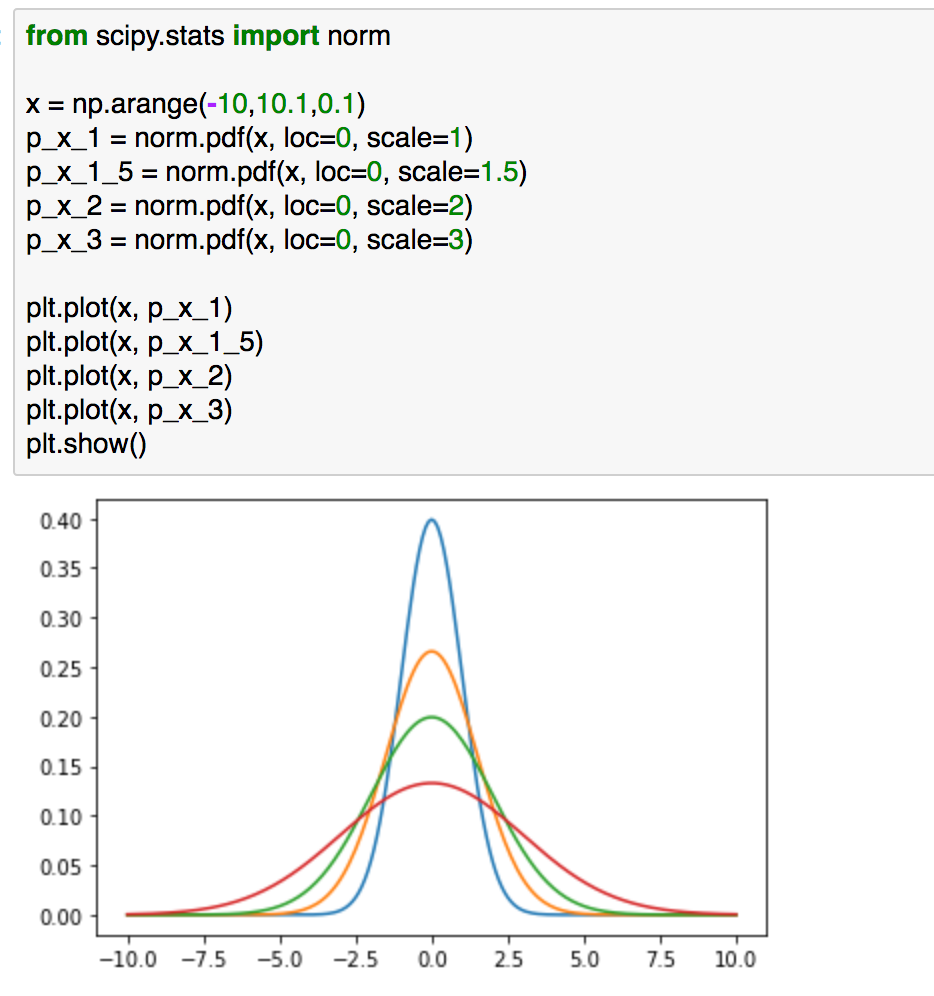
まずは問題設定として、上記を考えるとします。上記の4つの確率分布において、青の確率分布と近しい確率分布はどれかを考えるにあたってKLダイバージェンスを計算するとします。

KLダイバージェンスの計算は下記のように実装できます。

entropy_1 = - np.sum(p_x_1 * 0.1 * np.log(p_x_1/p_x_1))
entropy_1_5 = -np.sum(p_x_1 * 0.1 * np.log(p_x_1_5/p_x_1))
entropy_2 = -np.sum(p_x_1 * 0.1 * np.log(p_x_2/p_x_1))
entropy_3 = -np.sum(p_x_1 * 0.1 * np.log(p_x_3/p_x_1))

print(entropy_1)
print(entropy_1_5)
print(entropy_2)
print(entropy_3)

f:id:lib-arts:20201022201547p:plain
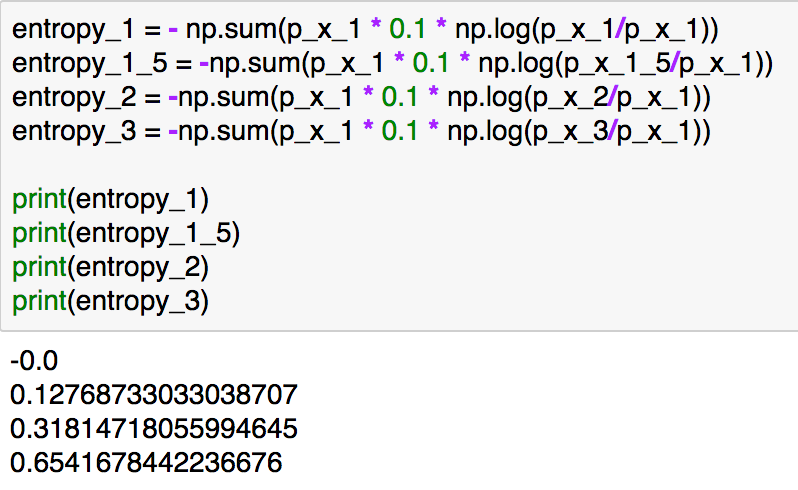
実行結果は上記のようになります。分散の値が同じ分布ではKLダイバージェンスは0、近い分布では値が小さく、分散の値が大きくなるにしたがってKLダイバージェンスの値は大きくなっています。（-10より小さい区間や10より大きい区間を取り扱わないなど、簡易化のためいくつか近似を行っていますが、概要を掴むのが目的のため細かいところの厳密性はここでは無視してください。）

3. まとめ
#1ではエントロピーとKLダイバージェンスの数式の確認や実装などを行いました。KLダイバージェンスは「確率分布を簡単な分布で近似するにあたって導入する、確率分布の類似度」とざっくり把握しておくと良いかと思います。
#2ではイェンセンの不等式と凸関数について考えつつ、KLダイバージェンスについて考察してみようと思います。