2020-10-25

対数尤度における指数型分布族を考える｜Python実装で理解する変分推論(VariationalInference) #Appendix2

f:id:lib-arts:20201022172002p:plain

#3、#4ではEMアルゴリズムについて取り扱いましたが、例として出てくる正規分布などを一般化した分布である指数型分布族についてもう少し考えておくと良いと思われたため、Appendix2としてまとめます。
以下、目次になります。
1. EMアルゴリズムにおける指数型分布族の記述について
2. 指数型分布族と対数尤度
3. まとめ

1. EMアルゴリズムにおける指数型分布族の記述について
1節ではEMアルゴリズムにおける指数型分布族の記載について簡単に確認しようと思います。

f:id:lib-arts:20201024191403p:plain

f:id:lib-arts:20201024191420p:plain

1つ目の記載は(9.29)式の後になります。「同時分布(joint distribution)のp(X|θ)におけるsum(和; Σ)によってlogarithm(log)が直接作用することを妨げる」と記載されています。混合分布の割合を表すπにより、#4の(9.14)式→(9.16)式のような計算が複雑になるということについて示唆しています。

f:id:lib-arts:20201024191433p:plain

2つ目の記載は(9.36)式の後になります。(9.36)式ではlogarithmが直接正規分布(Gaussian distribution)や指数型分布族(exponential family)に作用すると記載されています。(9.14)式の計算(主に微分)が難しい一方で、(9.36)式の計算が比較的容易であるともされています。

f:id:lib-arts:20201024191450p:plain

3つ目の記載は(9.74)式の後になります。同時分布のp(Z,X|θ)が指数型分布族やその積で表される時、logarithmは指数型分布族のexponentialと打ち消し合い、Mステップの計算が容易になると記載されています。EMアルゴリズムにおいて、Eステップはサンプルの割り当てを変え、Mステップがパラメータの最適化を行なっているので、Mステップの計算は基本的な流れでの最尤法と似たような式変形となります。なので、簡単なモデリングにおける最尤法やそれと同様のMステップにおいて、確率分布に指数型分布族を仮定することで確率分布におけるexponentialと対数尤度を考える際のlogarithmが打ち消しあうことで計算がスムーズになると理解して良いと思います。

1節では参照テキストのChapter9における指数型分布族(exponential family)の記載について確認してきましたが、「簡単なモデリングにおける対数尤度を計算するにあたって指数型分布族を確率分布として設定することで計算を簡単にすることができる」ということをここでは抑えておいてください。計算については2節で詳しく確認します。

2. 指数型分布族と対数尤度
2節では指数型分布族と対数尤度について確認します。

https://www.amazon.co.jp/dp/B08FYMTYBW

指数型分布族の記載については上記の2-2節に関連の式変形を載せていますので、こちらも合わせて参照ください。

まずは定義式から確認します。
$P(x|\theta) = exp\{a(x)b(\theta) + c(\theta) + d(x)\}$
指数型分布族は上記のように表すことのできる確率分布とされています。観測値の集合を $X=\{ x_1, x_2, ..., x_n \}$ とした際に、尤度は同時確率をパラメータについて着目したものと考えることができるので下記のように表すことができます。
$L(\theta) = P(X|\theta) = P(x_1, x_2, ..., x_n|\theta)$
$= P(x_1|\theta) \times P(x_2|\theta) \times ... \times P(x_n|\theta)$
上記は一般的な表記ですが、ここに $P(x_k|\theta) = exp\{a(x_k)b(\theta) + c(\theta) + d(x_k)\}$ を代入します。
$L(\theta) = P(X|\theta) = exp\{a(x_1)b(\theta) + c(\theta) + d(x_1)\} \times ... \times exp\{a(x_n)b(\theta) + c(\theta) + d(x_n)\}$
$\displaystyle = exp \left( \sum_{k=1}^{N} \{a(x_k)b(\theta) + c(\theta) + d(x_k) \} \right)$
指数型分布族に関する尤度L(θ)は上記のようになり、指数関数の中にΣがあるような式の形となります。
$\displaystyle log L(\theta) = \sum_{k=1}^{N} \{a(x_k)b(\theta) + c(\theta) + d(x_k) \}$
これに対する対数尤度は上記になります。なんとlogとexpが打ち消しあって、非常にシンプルな式として表記することができます。
$\displaystyle l_k = a(x_k)b(\theta) + c(\theta) + d(x_k)$
ここで上記のように $l_k$ を定義することで、 $\displaystyle \frac{dl_k}{d \theta}$ を計算した上で $\displaystyle \sum_{k=1}^{N} \frac{dl_k}{d \theta} = 0$ を解くと、非常にスムーズに確率分布のパラメータを求めることができます。
$\displaystyle log L(\theta) = \sum_{k=1}^{N} \{a(x_k)b(\theta) + c(\theta) + d(x_k) \}$
指数型分布族を考えるにあたっては、上記の対数尤度の式が非常にシンプルなので、こちらを計算した上で $\displaystyle l_k = a(x_k)b(\theta) + c(\theta) + d(x_k)$ を設定し、a〜dに用いる指数型分布族の式の形を代入するのが計算としてやりやすいと思います。
$\displaystyle a(x_k)=x_k$
$\displaystyle b(\mu)=\frac{\mu}{\sigma^2}$
$\displaystyle c(\mu)=-\frac{\mu^2}{2 \sigma^2}-\frac{1}{2}log(2 \pi \sigma^2)$
$\displaystyle d(x_k)=-\frac{x_{k}^2}{2 \sigma^2}$
例えば正規分布について、平均の $\mu$ を $\theta$ として考える際はa〜dは上記のように与えることができます。

対数尤度の導出がしんどいと感じるようでしたら、先に指数型分布族の式として対数尤度まで計算した上で後からa〜dを用いるというのも計算をシンプルに行うためのテクニックとしてありだと思います。

3. まとめ
Appendix2では指数型分布族の式における対数尤度を考えることで、式をシンプルに保ったまま式変形が行えることについてまとめました。式変形が複雑だと理解できるはずの内容まで理解できなくなるので、なるべくシンプルに記述することは様々な場面で役に立つのではないかと思います。

2020-10-24

EMアルゴリズムの論理構成の全体像｜Python実装で理解する変分推論(VariationalInference) #4

EM-Algorithm Machine Learning statistics

f:id:lib-arts:20201022172002p:plain

当シリーズはPython実装を通して変分推論を理解していこうということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

#3では変分推論の枠組みにおけるEMアルゴリズムを混合正規分布(Gaussian Mixture Models)を題材にしながら確認しました。

#3の論理展開が若干わかりづらいとも思われたため、#4ではEMアルゴリズムの論理構成の全体像について再度確認を行えればと思います。
以下、目次になります。
1. EMアルゴリズムの全体像まとめ
2. 変分推論への展開
3. まとめ

1. EMアルゴリズムの全体像まとめ
1節ではEMアルゴリズムの全体像のまとめについて行えればと思います。まず抑えておきたいのが正規混合分布(Gaussian Mixture)における、各正規分布の平均( $\mu$ )と分散( $\Sigma$ )、そして混合させるにあたってのそれぞれの割合( $\pi$ )のパラメータを推定するという問題設定です。

f:id:lib-arts:20201024173441p:plain

EMアルゴリズムは、上記における(9.14)式や(9.36)式のようなそれぞれのパラメータに関する尤度(Likelihood)の最適化のアルゴリズムであり、基本的には微分などを用いたアプローチによりパラメータの推定を行います。通常の流れでの正規混合分布における尤度は(9.14)式のようになるのですが、 $\ln$ の中に $\Sigma$ があるためこの式は少々取り扱いづらく、(9.14)を起点に(9.24)〜(9.27)の導出を行うのはなかなか大変です（(9.14)から(9.24)のベースになる(9.16)式の導出の計算が1行で済んでいるのですが、目の錯覚ということでポジティブに解釈しましょう）。

f:id:lib-arts:20201024180019p:plain

さて、(9.14)式のように $\mathbf{X}$ だけを元に尤度を取り扱うと計算が複雑になるので、それぞれのサンプルにおける分布の配分に関係する $\mathbf{Z}$ も導入し、 $\mathbf{X}$ と同様に考えることで尤度の式が(9.36)式のように尤度の式をシンプルに変更しています。が、ここで $\mathbf{Z}$ については観測の $\mathbf{X}$ とパラメータの $\mathbf{\theta}$ がわかっている状況での事後分布としてしか表現できないため(Zは観測できない)、(9.40)式のように尤度の期待値を考えるということをします。(9.14)式、(9.40)式のどちらにおいても $\mathbf{Z}$ の事後分布である負担率( $\gamma$ ; responsibility)を固定した上でそれぞれのパラメータに関して最適化を行えば、(9.24)〜(9.27)を導出することができます。

f:id:lib-arts:20201024180114p:plain

負担率については上記で示した(9.13)式で表されています。要は観測値の $\mathbf{X}$ がある上で、各分布のパラメータを固定すれば得られるということで、K-meansにたとえるなら各クラスタの平均ベクトルに基づいてサンプルの割り当てを決めるのと同様な操作を行います(ここがEステップに相当します)。

f:id:lib-arts:20201024181535p:plain
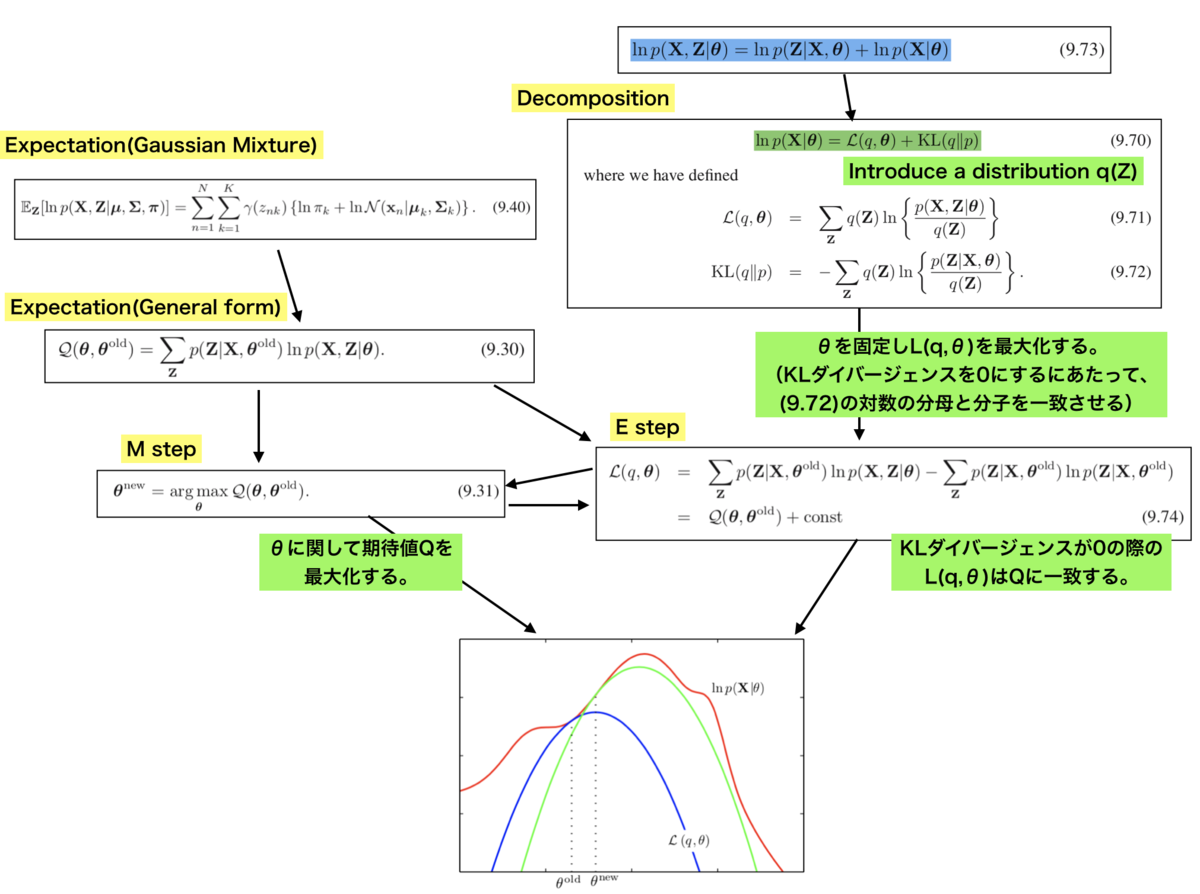
また、対数尤度の期待値については正規混合分布における(9.40)式から、一般的な式として上記の(9.30)式のように書き直すことができます。 $p(\mathbf{Z}|\mathbf{X}, \mathbf{\theta}^{old})$ が(9.13)式の負担率の定義と対応しています。この(9.30)式において $\mathbf{\theta}$ に関して最適化を行っているのが(9.31)式で示したMステップです。

また、ここでの議論を解釈するにあたって確率分布の $q(\mathbf{Z})$ を導入し、(9.70)式のような分解を行っています。(9.70)式については(9.71)式〜(9.73)式を用いることで導出が可能です。ここで重要なのが、(9.70)式において $L(q,\mathbf{\theta})$ を最大化するにあたってKLダイバージェンスを0にする条件として、 $q(\mathbf{Z})=p(\mathbf{Z}|\mathbf{X},\mathbf{\theta}^{old})$ を導出し、これを(9.71)に代入した結果として(9.74)式が得られるということです。これがEステップに相当するのですが、(9.74)式と(9.31)式の繰り返しとして全体のアルゴリズムを見ることにより、図におけるEMアルゴリズムの解釈が導出できます。Eステップでは $\mathbf{\theta}$ の値を固定して $L(q,\mathbf{\theta})$ をアップデートしていくため、青を緑に移動させるようなイメージです。また、Mステップでは $L(q,\mathbf{\theta})$ を最大化する $\mathbf{\theta}$ を導出します。

2. 変分推論への展開
2節ではここまでのEMアルゴリズムに関する議論をベースに、変分推論への展開を確認します。

f:id:lib-arts:20201024183044p:plain

上記のように、変分推論では(9.70)式で導入した $q(\mathbf{Z})$ に関しての取り扱いを考えていきます。(9.70)〜(9.72)を(10.2)〜(10.4)のように書き直して、 $q(\mathbf{Z})$ について議論を行っています。考え方としてメジャーなものとして、(10.5)のように $q(\mathbf{Z})$ を積の形に分解したmean-field的な考え方が紹介されています。

変分推論に関して詳しくは#5以降で取り扱うとして、今回はここまでとします。

3. まとめ
#4ではEMアルゴリズムの全体像について再度まとめながら変分推論への展開について簡単に確認しました。
#5以降では引き続き、変分推論について確認していければと思います。

2020-10-24

変分推論の枠組みにおけるEMアルゴリズム｜Python実装で理解する変分推論(VariationalInference) #3

Machine Learning Python statistics

f:id:lib-arts:20201022172002p:plain

当シリーズはPython実装を通して変分推論を理解していこうということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

#1、#2ではKLダイバージェンスやイェンセンの不等式について確認を行いました。

#3では変分推論の枠組みにおけるEMアルゴリズムを混合正規分布(Gaussian Mixture Models)を題材にしながら確認していきます。主にBishop[2006]のSection9.2〜10.1の内容を参照します。
以下、目次になります。
1. 基礎的な理論の確認(変分推論とEMアルゴリズム)
2. 混合正規分布とEMアルゴリズム
3. まとめ

1. 基礎的な理論の確認(変分推論とEMアルゴリズム)
1節では変分推論とEMアルゴリズムに関する基本的な理論について確認します。

f:id:lib-arts:20201023173537p:plain

変分推論を考えるにあたってまず抑えておきたいのが上記の数式です。(9.70)式における $\ln p(\mathbf{X} | \mathbf{\theta})$ は対数尤度を表しており、通常の最尤推定(MLE; Maxmum Likelihood Estimation)は対数尤度をパラメータ $\mathbf{\theta}$ に対して最大化します。ここでは通常の最適化問題とは異なり、潜在変数(latent variables)の $\mathbf{Z}$ に対して確率分布の $q(\mathbf{Z})$ を導入することで、 $L(q,\mathbf{\theta})$ と $KL(q||p)$ の和の形に対数尤度を変形しています。 $L(q,\mathbf{\theta})$ と $KL(q||p)$ についてはそれぞれ(9.71)と(9.72)のように表現されています。（(9.70)の導出については基本的に前後の記載をそのまま用いているのでここでは省略します）

さて、ここで $L(q,\mathbf{\theta})$ を考えるにあたって注意しておくと良いのが、 $L(q,\mathbf{\theta})$ はパラメータ $\mathbf{\theta}$ に関する関数であるのと同時に、確率分布 $q(\mathbf{Z})$ に関する汎関数(functional)であるということです。汎関数は以前の記事でも述べましたが、関数を入力として値を返す関数です。（この時点で何かしらの変分法的な取り扱いが行われることがわかります。）

f:id:lib-arts:20201023175744p:plain

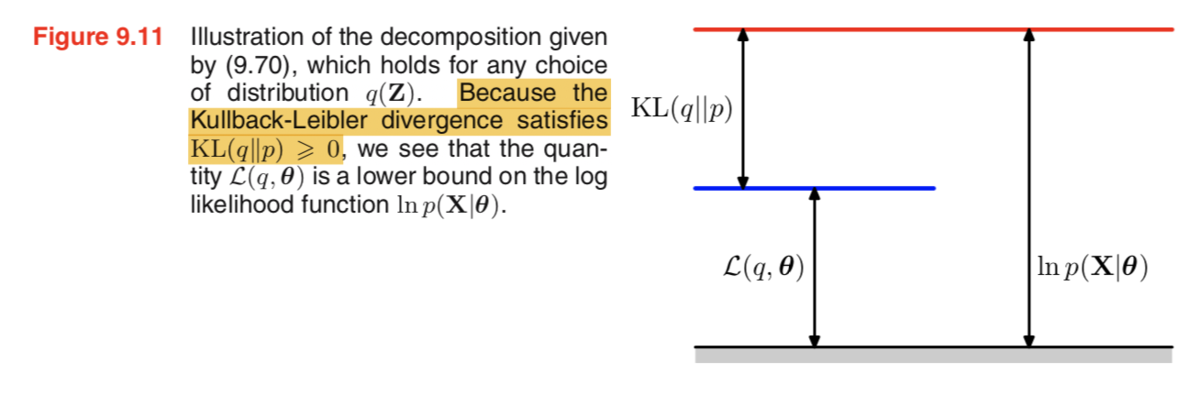
(9.70)式を図的なイメージで表すと上記のようになります。これは化学式などでエネルギーを考慮する際に用いる図と基本的には同じです。

f:id:lib-arts:20201023180652p:plain

f:id:lib-arts:20201023180712p:plain

EMアルゴリズムにおけるEステップの解釈は上記になります。パラメータの $\mathbf{\theta}$ (混合正規分布だと、各正規分布の平均や分散に相当)を固定した上で $q(\mathbf{Z})$ に対して $L(q,\mathbf{\theta}^{old})$ を最大化します。より具体的には $\mathbf{\theta}$ を $\mathbf{\theta}^{old}$ に固定した状況におけるKLダイバージェンスを0にします。KLダイバージェンスを0にするにあたっては $\ln$ の中を全ての要素に対して1にする必要があるので、 $q(\mathbf{Z})$ と $q(\mathbf{Z}|\mathbf{X},\mathbf{\theta}^{old})$ を一致させる必要があります。こうすることでFigure9.12の青矢印のように固定した $\mathbf{\theta}^{old}$ に関してlower boundを最大化させることができます。

f:id:lib-arts:20201023182412p:plain

f:id:lib-arts:20201023182639p:plain

一方Mステップの解釈は上記とされています。

f:id:lib-arts:20201023183112p:plain

f:id:lib-arts:20201023183126p:plain

f:id:lib-arts:20201023183142p:plain

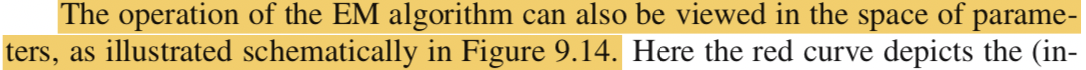
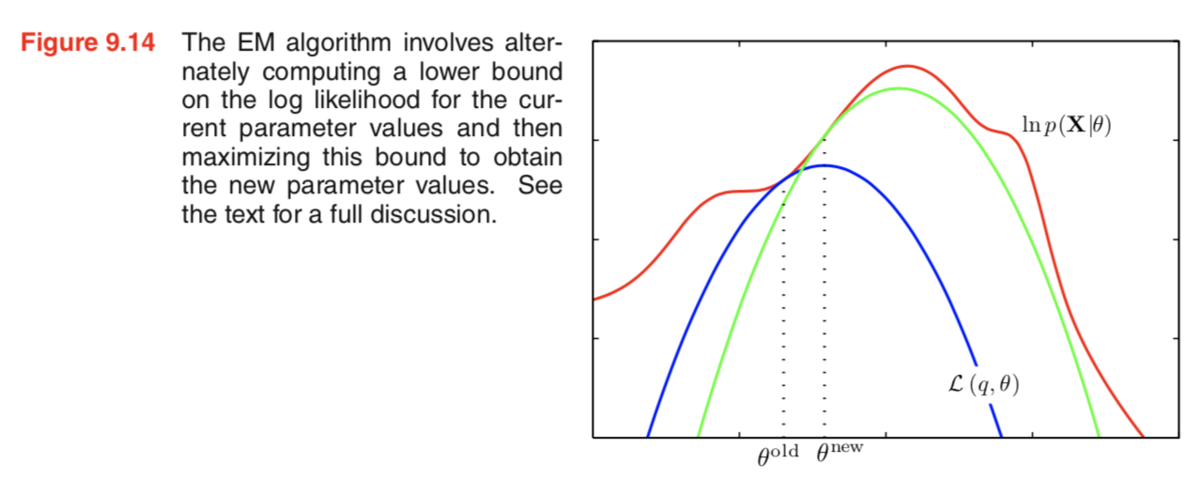
パラメータ空間におけるEMアルゴリズムの処理概要は上記とされています。Eステップでは $\mathbf{\theta}^{old}$ において赤と青の分布を一致させ、Mステップでは青の分布を最大にする $\mathbf{\theta}$ を求め、 $\mathbf{\theta}^{new}$ としています。

大体の流れがつかめたので、2節では具体的に混合正規分布をここまでの流れにあてはめて理解していきます。

2. 混合正規分布とEMアルゴリズム
2節では混合正規分布を題材にEMアルゴリズムについて確認していきます。

f:id:lib-arts:20201023200429p:plain

f:id:lib-arts:20201023200447p:plain

まず、一般的な意味合いでのEMアルゴリズムの記載は上記のようになります。Mステップにおいて(9.33)式の $Q(\mathbf{\theta},\mathbf{\theta}^{old})$ はサンプルの負担率(responsibility)を固定した上での対数尤度と同様の役割をしています。一方、Eステップでは $\mathbf{\theta}^{old}$ を固定した上で負担率(responsibility)の再計算を行っています。

f:id:lib-arts:20201023201751p:plain

f:id:lib-arts:20201023202033p:plain

また、混合正規分布におけるEMアルゴリズムは上記のようになります。Mステップは負担率を固定した上で、パラメータに尤度の最大化を行うことで導出しています。

記載だけで理解するのは大変なので、以下、実装を通してイメージを掴みます。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
%matplotlib inline

x_1 = norm.rvs(loc=0, scale=1, size=600, random_state=None)
x_2 = norm.rvs(loc=-3, scale=1, size=300, random_state=None)
x_3 = norm.rvs(loc=5, scale=2, size=100, random_state=None)
observed_x = np.r_[x_1, x_2, x_3]

plt.hist(observed_x, bins=20)
plt.show()

f:id:lib-arts:20201023221634p:plain

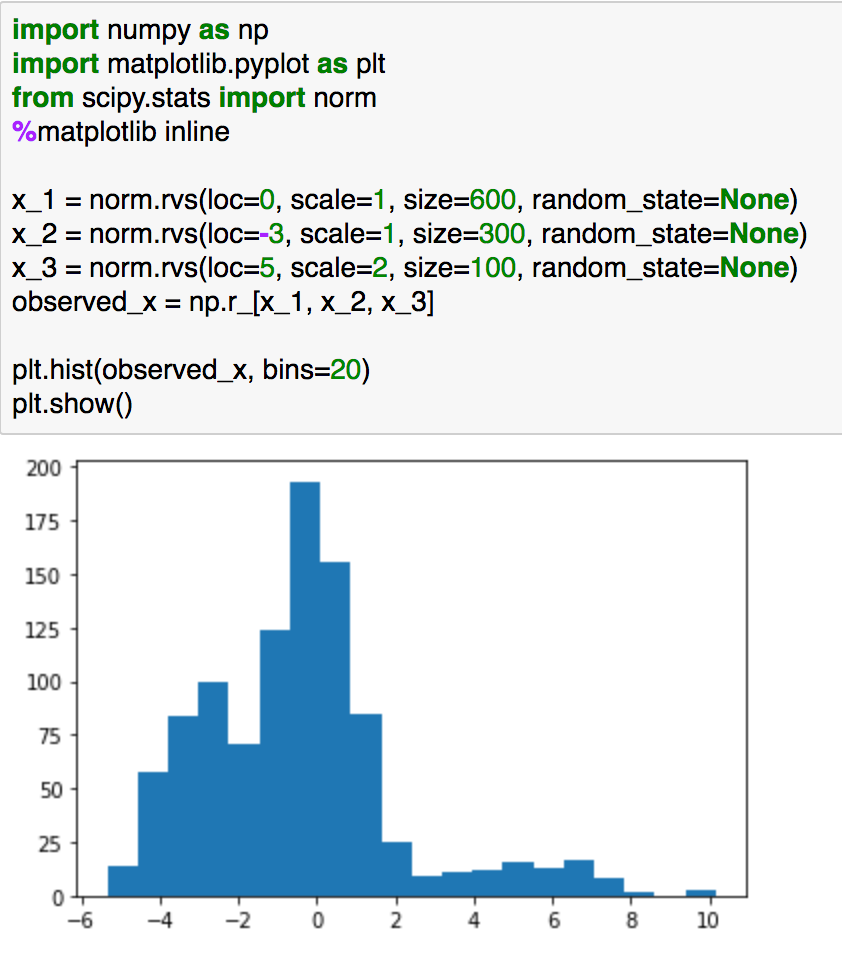
問題設定については上記のようなヒストグラムの観測が得られた際の背景にある混合分布の推定を行います。この分布は下記の混合正規分布からサンプリングしたのと同様な結果になります(累積分布関数の逆関数からサンプリングする考え方もありますが、簡易化のためこのようなサンプリングとしました)。

f:id:lib-arts:20201023222039p:plain

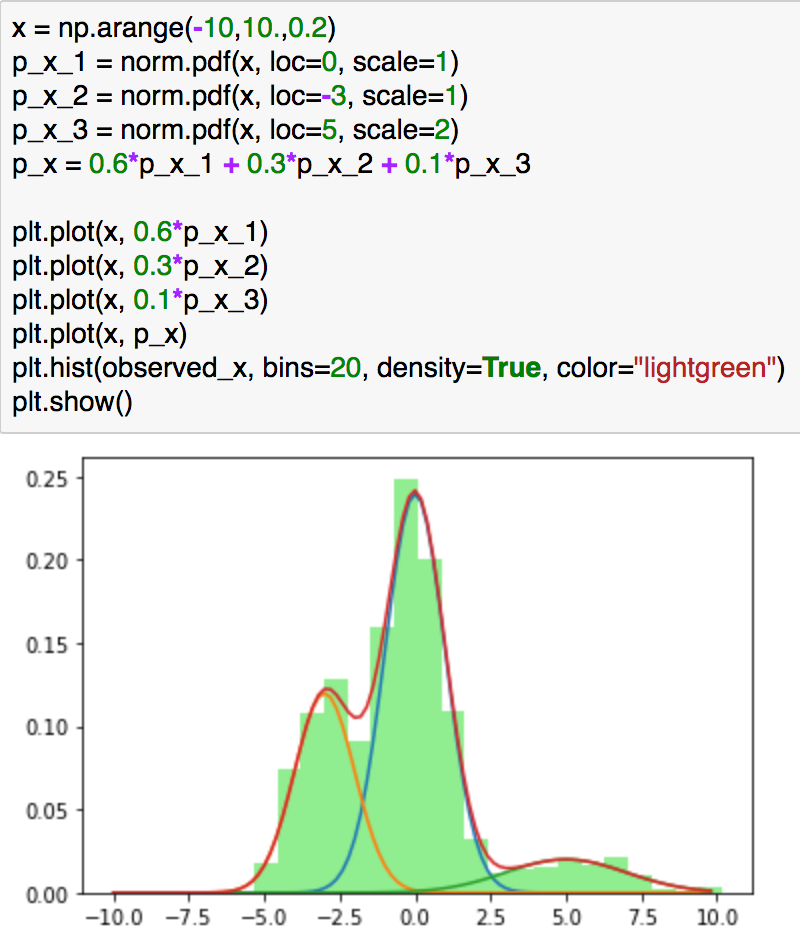
上記でイメージがつきやすいかと思います。

f:id:lib-arts:20201023222419p:plain

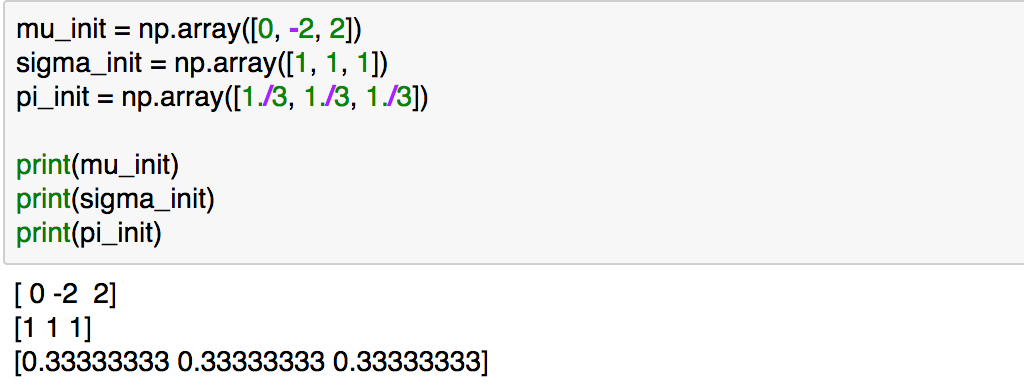
上記のように初期値を与え、下記を実行します(簡易化のため、分散は1で固定しました)。

pi = pi_init
mu = mu_init
sigma = sigma_init
gamma = np.zeros([observed_x.shape[0], 3])
for i in range(10):
# E-step
for j in range(observed_x.shape[0]):
for k in range(3):
gamma[j, k] = pi[k] * norm.pdf(observed_x[j], loc=mu[k], scale=sigma[k])
gamma[j, :] = gamma[j, :]/np.sum(gamma[j, :])
# M-step
N_k = np.zeros([3])
for k in range(3):
N_k[k] = np.sum(gamma[:, k])
pi[k] = N_k[k]/1000.
mu[k] = np.sum(gamma[:, k] * observed_x)/N_k[k]
print(N_k)
print(mu)
print("====")

f:id:lib-arts:20201023222448p:plain

実行結果を確認すると混合分布の推定が概ねうまくいっていることがわかります。

3. まとめ
#3では変分推論を念頭に置きながらEMアルゴリズムについて確認を行いました。
続く#4ではEMの全体像について確認し、論旨の流れを再度確認できればと思います。

2020-10-23

ベクトル的取り扱いによるイェンセンの不等式の図的理解｜Python実装で理解する変分推論(VariationalInference) #Appendix1

Machine Learning Math statistics Python

f:id:lib-arts:20201022172002p:plain

#2ではイェンセンの不等式とKLダイバージェンスの非負性について取り扱いましたが、少し考察が定性的になりましたので、もう少しイェンセンの不等式ベースでわかりやすくしようということで、Appendixを設けました。
3つ以上の $\lambda_{i}$ や $p(x_{i})$ に対する取り扱いのイメージが少々付きづらいのと、KLダイバージェンスの $\ln$ の中身が $\displaystyle \frac{q(x)}{p(x)}$ という風になっているのでややこしく見えるというのがあるためです。

f:id:lib-arts:20201022221816p:plain

f:id:lib-arts:20201022222407p:plain

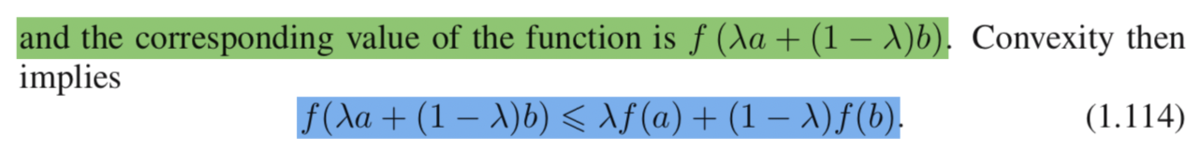
この記事では上記で表すことのできるイェンセンの不等式をベクトルの和として取り扱うことにより、より直感的な理解が可能になるようにということでまとめます。
以下、目次になります。
1. ベクトルの和と直線上の点
2. 3つ以上の点がある際のイェンセンの不等式のベクトル的取り扱い
3. まとめ

1. ベクトルの和と直線上の点
1節ではベクトルの和と直線について、数式を元に簡単に考えてみます。まず、基本的な事項として、始点(位置ベクトルなので基本的に原点で考えていればよい)を揃えた際のベクトルの和は、それぞれの係数の和が1の場合は終点を結ぶ直線上に存在します。数式で導出すると下記のようになります。
$\overrightarrow{OP} = \lambda \overrightarrow{OA} + (1 - \lambda) \overrightarrow{OB} = \overrightarrow{OB} + \lambda (\overrightarrow{OA} - \overrightarrow{OB}) = \overrightarrow{OB} + \lambda \overrightarrow{BA}$
上記において位置ベクトル $\overrightarrow{OP}$ を持つ点Pはイェンセンの不等式(1.114)の右辺の数式に対応しており、 $\overrightarrow{OB} + \lambda \overrightarrow{BA}$ で位置ベクトルが表されていることからこれは線分AB( $\lambda$ が0以上1以下だから線分になる)上の点になります。

f:id:lib-arts:20201022224441p:plain

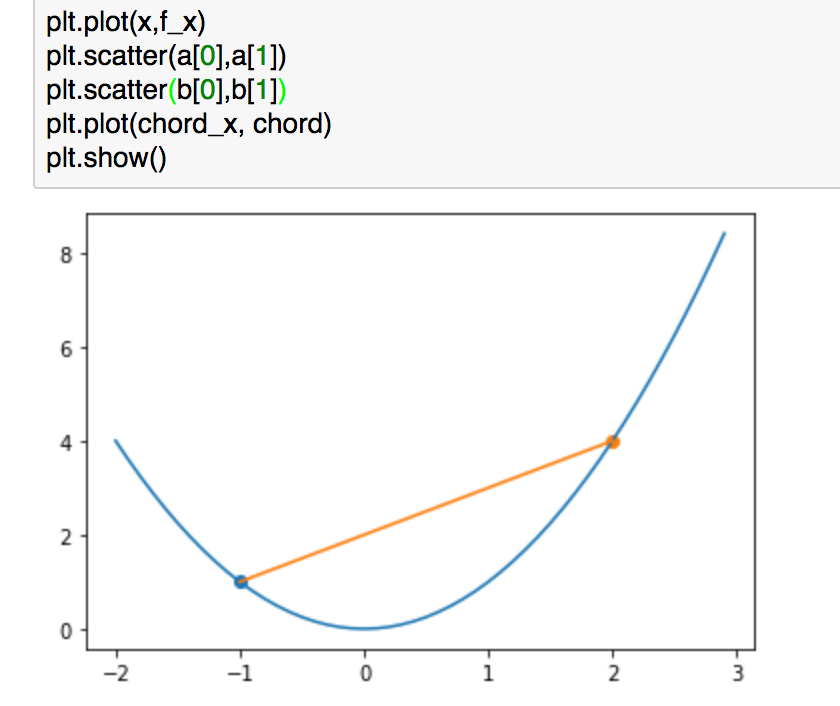
上記は#2で用いた例ですが、こちらでもう少し考えてみます。

def calc_P(lam):
OP_x = lam*a[0] + (1-lam)*b[0]
OP_y = lam*a[1] + (1-lam)*b[1]
print("P: ({:.2f}, {:.2f})".format(OP_x, OP_y))
plt.scatter(OP_x,OP_y, color="blue")
plt.scatter(OP_x,OP_x**2, color="black")

plt.plot(x,f_x)
plt.scatter(a[0],a[1], color="green")
plt.scatter(b[0],b[1], color="green")
plt.plot(chord_x, chord)

calc_P(0.3)
calc_P(0.5)
calc_P(0.9)
plt.plot(x,f_x)
plt.show()

f:id:lib-arts:20201023150534p:plain

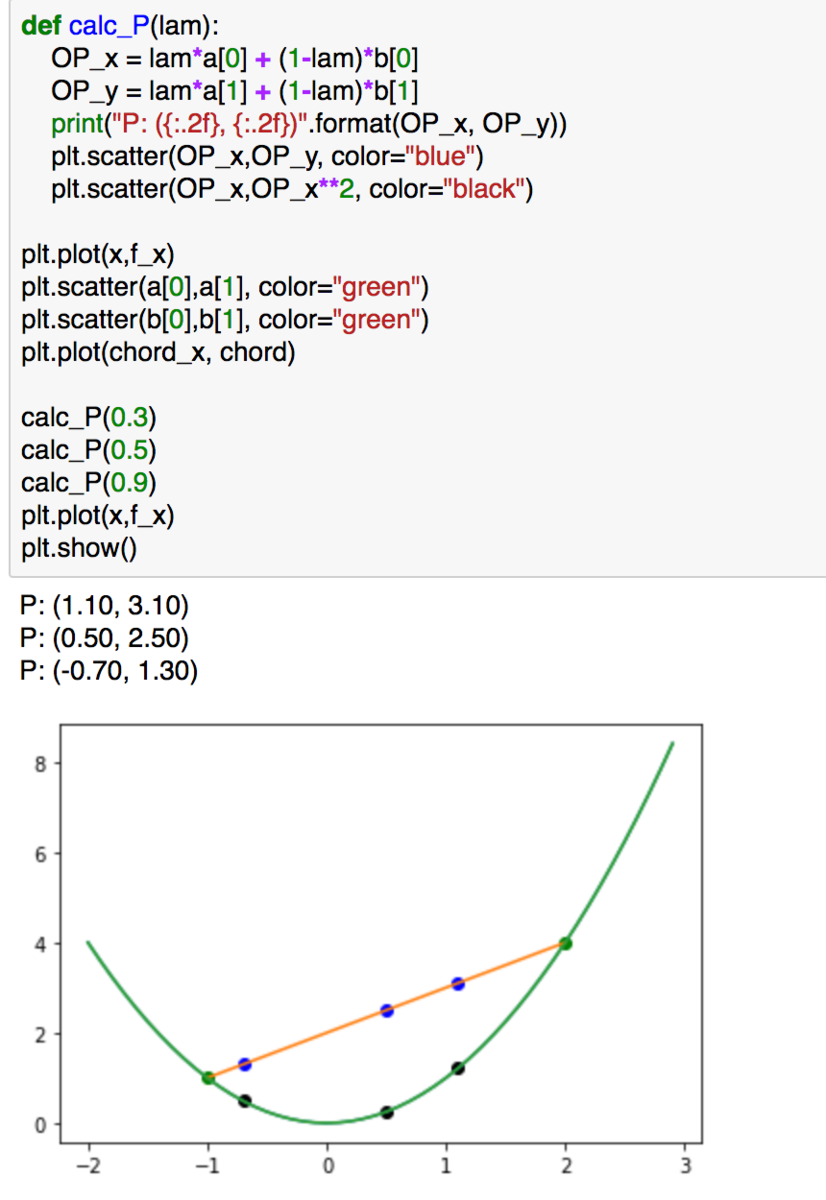
上記の青色の点に着目することで"calc_P(lam)"を用いて、線分AB上の点が表現できていることが確認できるかと思います。また、各xの値に対応する青の点と黒の点の大小関係についての不等式がイェンセンの不等式になります。

ベクトルの和とイェンセンの不等式のイメージがついたかと思いますので1節はここまでとします。

2. 3つ以上の点がある際のイェンセンの不等式のベクトル的取り扱い
1節は2点におけるイェンセンの不等式の取り扱いについて見てきました。
$\overrightarrow{OP} = \lambda \overrightarrow{OA} + (1 - \lambda) \overrightarrow{OB} = \overrightarrow{OB} + \lambda (\overrightarrow{OA} - \overrightarrow{OB}) = \overrightarrow{OB} + \lambda \overrightarrow{BA}$
上記で表現できるように、イェンセンの不等式(1.114)の右側をベクトルで表すことで直線上の点であることを表現できます。

ここまでが1節の内容の確認ですが、ここでAとBだった二つの点の数を増やすとどのようになるのでしょうか。まずは3つの点で考えてみます。
$\overrightarrow{OP} = \lambda_{1} \overrightarrow{OA} + \lambda_{2} \overrightarrow{OB} + \lambda_{3} \overrightarrow{OC}$
$\lambda_{1} + \lambda_{2} + \lambda_{3} = 1$
数式としてはイェンセンの不等式(1.115)の右辺を元に、上記を考えていくものとします。ベクトルの和については1節と同様に考えることで下記のように計算できます。 $\overrightarrow{OP} = \lambda_{1} \overrightarrow{OA} + \lambda_{2} \overrightarrow{OB} + \lambda_{3} \overrightarrow{OC} = \overrightarrow{OA} + \lambda_{2}(\overrightarrow{OB}-\overrightarrow{OA}) + \lambda_{3}(\overrightarrow{OC}-\overrightarrow{OA})$
$= \overrightarrow{OA} + \lambda_{2} \overrightarrow{AB} + \lambda_{3} \overrightarrow{AC}$

ここで $(\lambda_{2}+\lambda_{3})\overrightarrow{AB}=\overrightarrow{AB'}$ 、 $(\lambda_{2}+\lambda_{3})\overrightarrow{AC}=\overrightarrow{AC'}$ となるように $B'$ と $C'$ を考えると、点Pは線分 $B'C'$ 上の点となります。線分 $B'C'$ は三角形ABCの内部に存在するため、点が2つの際と同様にイェンセンの不等式が成立することがわかります。点が3つより多い場合でも同様に議論ができるためイェンセンの不等式は成立します。

数式ばかりわかりづらいと思うので、簡単に図でも確認してみます。

f:id:lib-arts:20201023155104p:plain

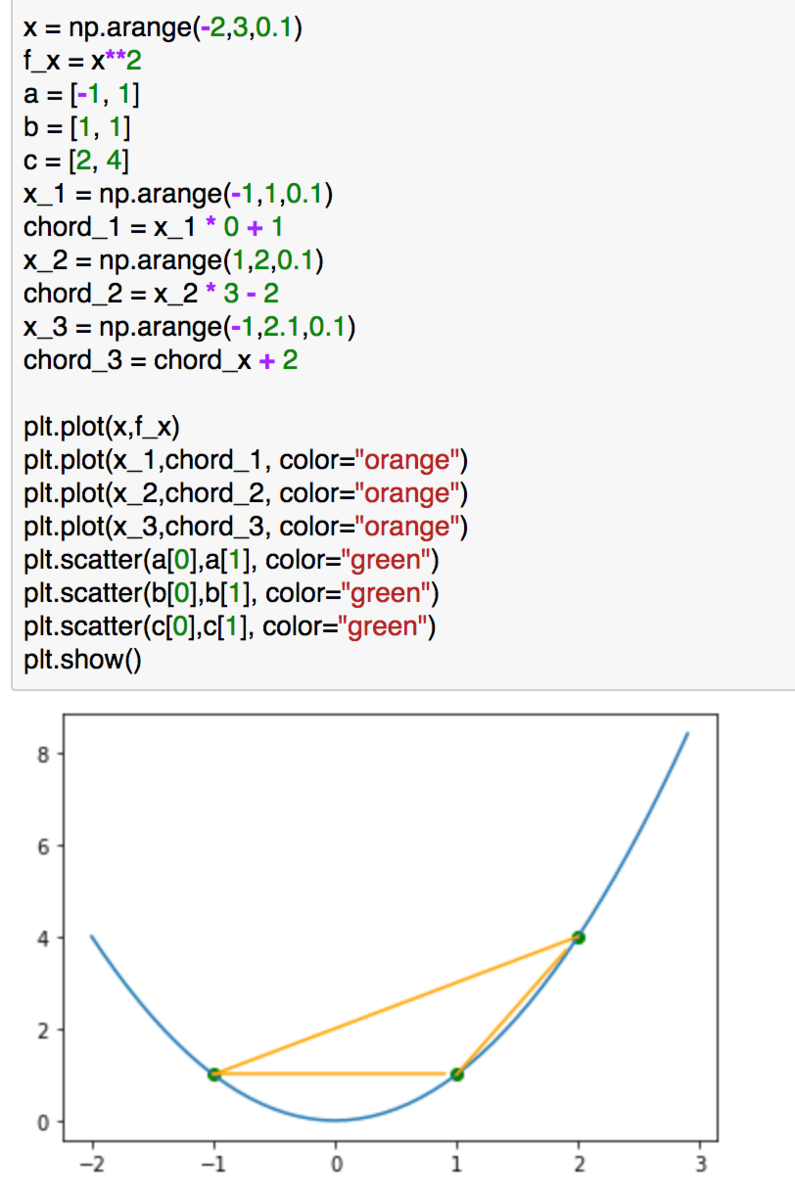
上記のような問題設定で考えるとします。関連の計算は下記によって実行できます。

def calc_P(lam1, lam2, lam3):
OP_x = lam1*a[0] + lam2*b[0] + lam3*c[0]
OP_y = lam1*a[1] + lam2*b[1] + lam3*c[1]
print("P: ({:.2f}, {:.2f})".format(OP_x, OP_y))
plt.scatter(OP_x,OP_y, color="blue")
plt.scatter(OP_x,OP_x**2, color="black")

plt.plot(x,f_x, color="dodgerblue")
plt.plot(x_1,chord_1, color="orange")
plt.plot(x_2,chord_2, color="orange")
plt.plot(x_3,chord_3, color="orange")
plt.scatter(a[0],a[1], color="green")
plt.scatter(b[0],b[1], color="green")
plt.scatter(c[0],c[1], color="green")

calc_P(0.3, 0.3, 0.4)
calc_P(0.6, 0.2, 0.2)
plt.plot(x,f_x)
plt.show()

f:id:lib-arts:20201023160113p:plain

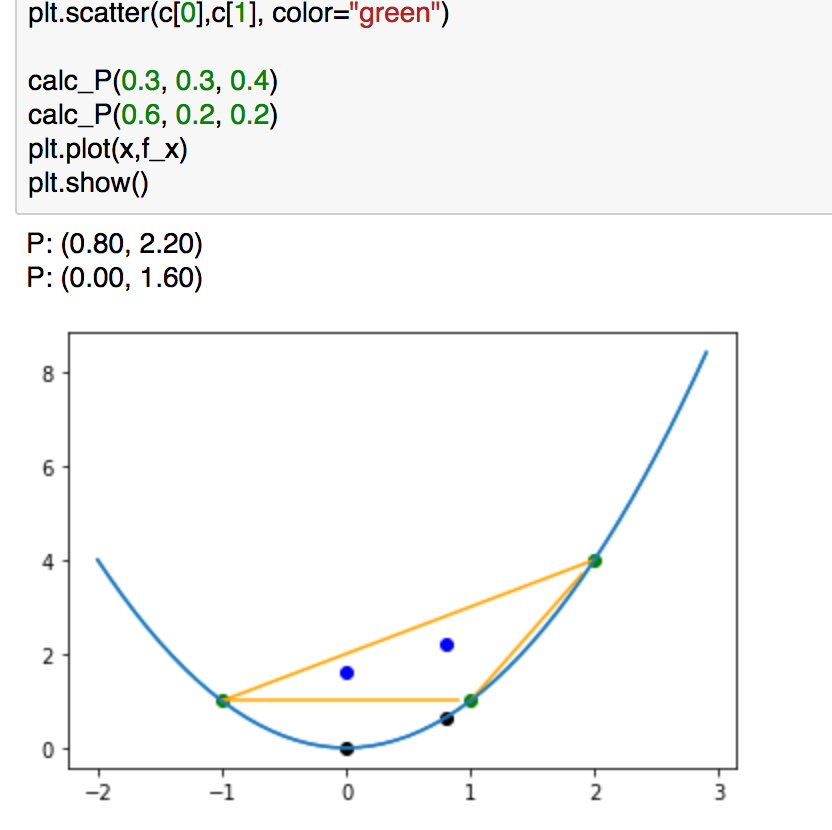
上記の青の点がオレンジの三角形の中に入っていることと、対応する黒の点よりも上にいることが確認できるかと思います。上記からイェンセンの不等式が成立している(三角形ABCは凸関数よりも上にある)ことを図的に理解できるかと思います。

3. まとめ
Appendix1ではベクトルの和について考えることで、イェンセンの不等式の図的な理解を行いました。点が3つ以上のケースが混乱しがちだと思いますが、ベクトルをベースで考えることで不等式のイメージが掴みやすくなったかと思います。

2020-10-23

イェンセンの不等式とKLダイバージェンスの非負性｜Python実装で理解する変分推論(VariationalInference) #2

statistics Python Machine Learning

f:id:lib-arts:20201022172002p:plain

当シリーズはPython実装を通して変分推論を理解していこうということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

#1では変分推論の議論の中心となってくるKLダイバージェンスについて確認しました。

#2ではKLダイバージェンスの非負性(必ず0以上になる)を考えるにあたって、イェンセンの不等式を元にした導出を追いつつ、簡単に実装でも表現してみます。
以下目次になります。
1. イェンセンの不等式
2. KLダイバージェンスの非負性の導出
3. まとめ

1. イェンセンの不等式(Jensen’s inequality)
1節ではイェンセンの不等式(Jensen’s inequality)について取り扱います。

f:id:lib-arts:20201022221318p:plain

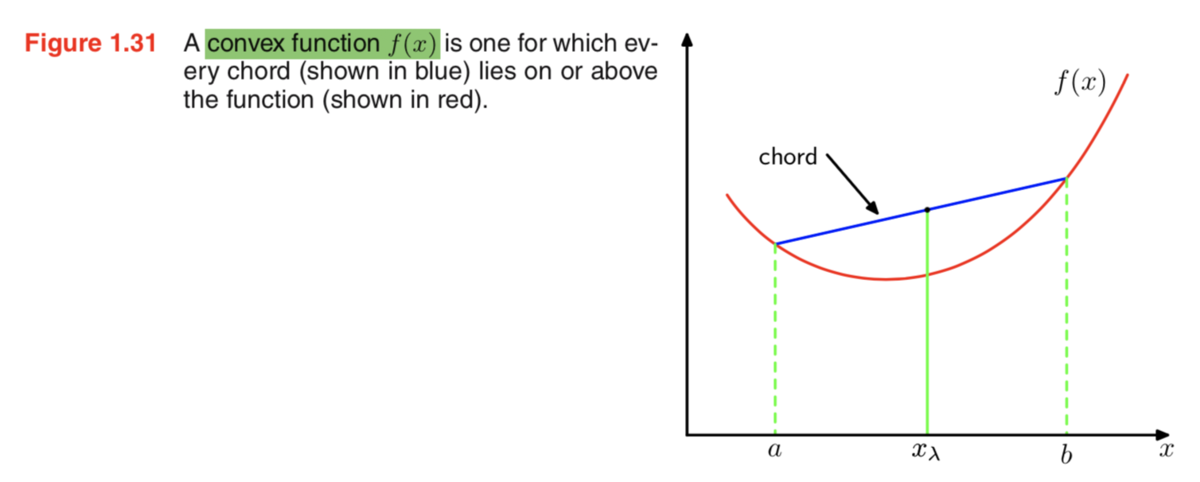
イェンセンの不等式は上記のような凸関数(convex function)とその弦(chord)について成立する不等式です。ざっくり把握するなら、弦(chord)上の点は同一のx座標における凸関数上の点よりも上に来るということです。

f:id:lib-arts:20201022221732p:plain

f:id:lib-arts:20201022221816p:plain
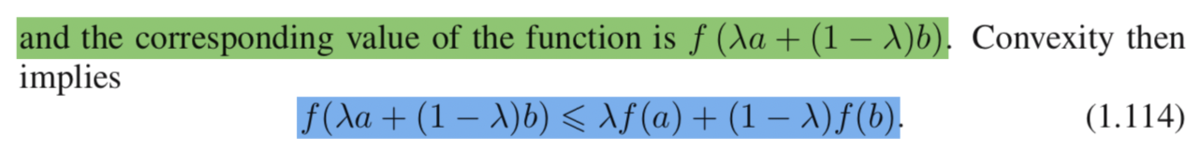
イェンセンの不等式を数式的に表すなら上記の(1.114)式のようになります。少しややこしい式ではありますが、図における $x_{\lambda}$ における弦上の点と凸関数上の点の位置関係に関する不等式となっていると解釈すれば十分です。ここで $\lambda$ は $a$ と $b$ のどちらに近いかなどを表すパラメータです。

f:id:lib-arts:20201022222407p:plain

また、イェンセンの不等式は上記のようにも考えることができます。(1.115)は3つ以上の点について取り扱うこともできるように拡張しており、(1.116)は $\lambda$ を確率分布に対応させることで期待値としてイェンセンの不等式を表しています。続く(1.117)では連続変数(continuous variable)にイェンセンの不等式を適用しています。

ここで、イェンセンの不等式の数式がややこしくなると思うのでもう一度改めて整理を行います。イェンセンの不等式を成立させるにあたって一番重要なポイントとしては、 $\displaystyle \sum_{i=1}^{M} \lambda_{i}=1$ が成立しているということです。したがって、(1.115)を考える際には $\lambda$ 、(1.116)と(1.117)を考えるにあたっては $p(x)$ が非常に重要になります。

さて、数式の議論が続きややこしくなってきたと思いますので、以下実装について見ていきます。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(-2,3,0.1)
f_x = x**2
a = [-1, 1]
b = [2, 4]
chord_x = np.arange(-1,2.1,0.1)
chord = chord_x + 2

plt.plot(x,f_x)
plt.scatter(a[0],a[1])
plt.scatter(b[0],b[1])
plt.plot(chord_x, chord)
plt.show()

まず凸関数において、上記のようにすることで問題設定を再現することができます。

f:id:lib-arts:20201022224441p:plain

実行結果は上記のようになります。図については確認できたので、以下では具体的に $\lambda$ を用いた式を用いながら確認を行っていきます。

def calc_Jensen(a, b, f_a, f_b, lam):
chord = lam*f_a + (1-lam)*f_b
f_x = (lam*a + (1-lam)*b)**2
print("chord:{:.2f}, f_x:{:.2f}".format(chord, f_x))

calc_Jensen(-1,2,1,4,0.1)
calc_Jensen(-1,2,1,4,0.2)
calc_Jensen(-1,2,1,4,0.5)
calc_Jensen(-1,2,1,4,0.8)
calc_Jensen(-1,2,1,4,0.9)
calc_Jensen(-1,2,1,4,1.)

実行結果は下記になります。

f:id:lib-arts:20201022225624p:plain

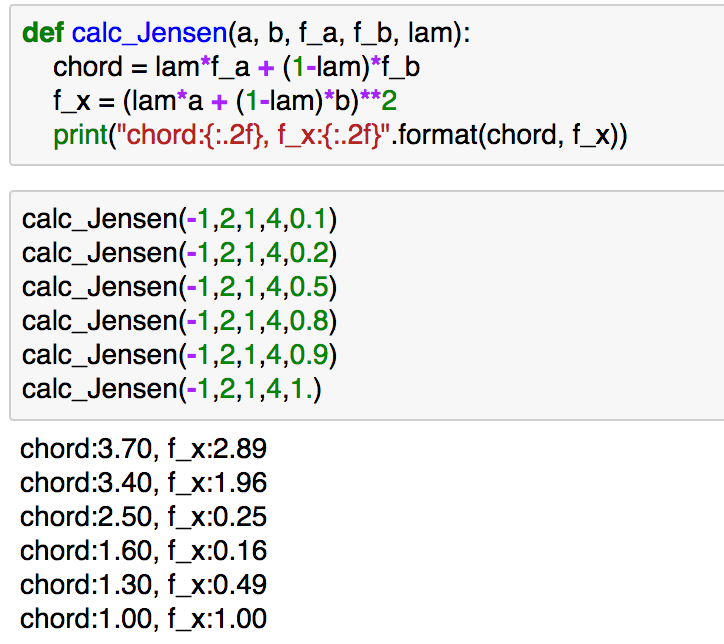
上記では様々な $\lambda$ の値に対して、イェンセンの不等式が成立しているのが確認できるかと思います。

2. KLダイバージェンスの非負性の導出
2節ではKLダイバージェンスの非負性の導出について確認します。

f:id:lib-arts:20201022230142p:plain

f:id:lib-arts:20201022230210p:plain

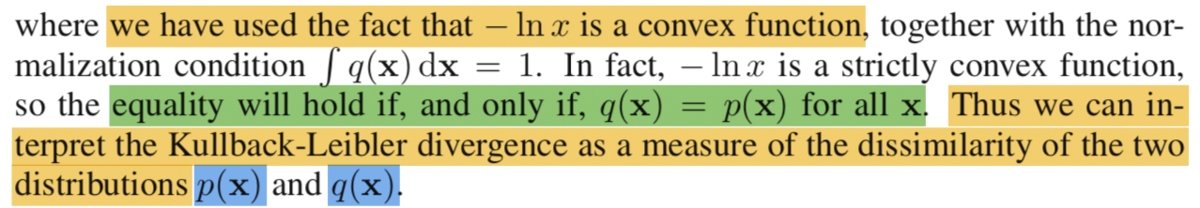
導出は上記のようになります。ここで、式(1.118)の解釈が難しいかもしれませんが、 $f(x)=-ln x$ 、 $\displaystyle g(x) = \frac{q(x)}{p(x)}$ のようにすると、積分の中の式を $-p(x)f(g(x))$ のように置き換えることができます。
$\displaystyle \int p(x) \ln \frac{p(x)}{q(x)} dx = -\int -p(x)f(g(x)) dx = \int p(x)f(g(x)) dx$
$\displaystyle \geqq f \left(\int p(x)g(x) dx \right) = -\ln \int p(x) \frac{q(x)}{p(x)} dx = -\ln \int q(x) dx = 0$
式(1.118)は確率分布の $p(x)$ と凸関数の $- \ln(x)$ に着目することで上記のような変換を行っています。ここでの式変形は混乱しやすいかもしれません。

f:id:lib-arts:20201022200517p:plain

f:id:lib-arts:20201022201547p:plain

実装については#1で取り扱っているのでこちらをもう少し詳しく確認してみます。

entropy_1 = - p_x_1 * 0.1 * np.log(p_x_1/p_x_1)
entropy_1_5 = - p_x_1 * 0.1 * np.log(p_x_1_5/p_x_1)
entropy_2 = - p_x_1 * 0.1 * np.log(p_x_2/p_x_1)
entropy_3 = - p_x_1 * 0.1 * np.log(p_x_3/p_x_1)

plt.scatter(x, entropy_1)
plt.scatter(x, entropy_1_5, color="red")
plt.scatter(x, entropy_2, color="green")
plt.scatter(x, entropy_3, color="orange")
plt.show()

f:id:lib-arts:20201022234403p:plain

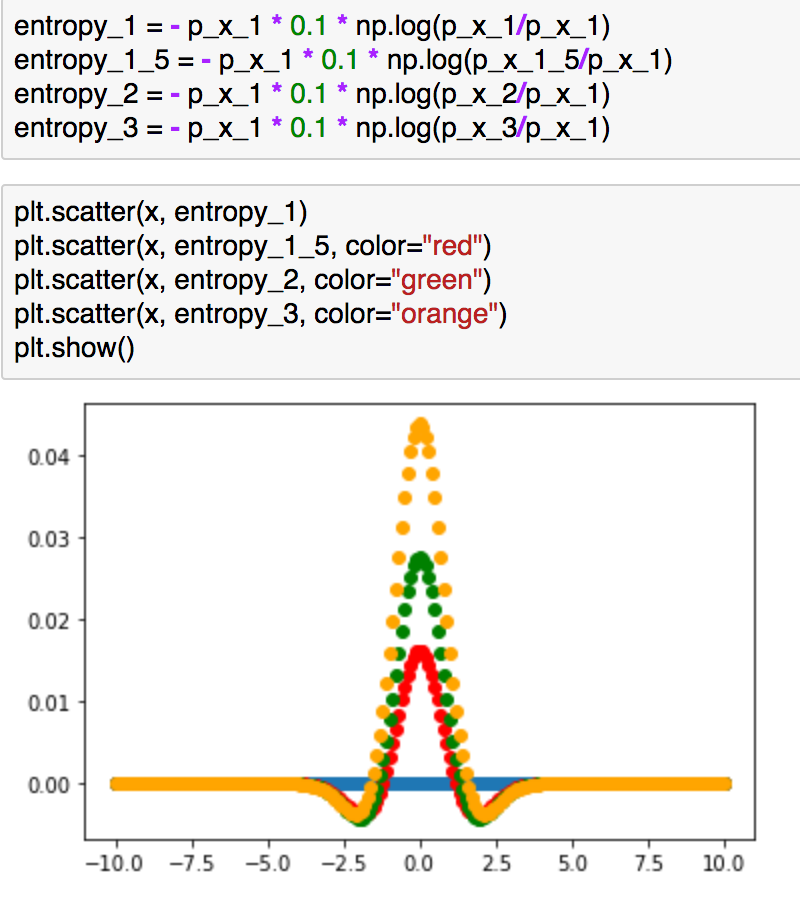
上記は、和の計算を行う前の値をプロットしたものです。分散の値の差が大きい方が(この場合のKLダイバージェンスは大きい)、0付近の値の差が大きく、これが理由でKLダイバージェンスの大きさが異なっていると考えることができるかと思います。こちらについては定性的な考察ではありますが、概要を掴むにあたっては時にはこのような考察も有意義かと思います。

3. まとめ
#2ではイェンセンの不等式とKLダイバージェンスの非負性について議論を行いました。
#3では、変分推論の文脈におけるEMアルゴリズムについて確認を行えればと思います。

2020-10-22

KLダイバージェンスの数式とPython実装｜Python実装で理解する変分推論(VariationalInference) #1

Python statistics Machine Learning

f:id:lib-arts:20201022172002p:plain

確率的変分推論(SVI; Stochastic Variational Inference)の論文について確認していたのですが、ベースの理解についてもう少し固める方が良さそうだったので、Python実装を通して変分推論を理解していくシリーズを新たに作成することにしました。シリーズを通してPattern Recognition and Machine Learning(Bishop, 2006)を主に参照しつつ、実装を作成します。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

#1では変分推論の議論の中心となってくるKLダイバージェンスについて確認します。Bishop[2006]のSection1-6の内容を基本的に参考にします。
以下目次になります。
1. エントロピーについて
2. KLダイバージェンスについて
3. まとめ

1. エントロピーについて
1節ではエントロピー(entropy)について確認します。

f:id:lib-arts:20201022172206p:plain

まず離散的なエントロピーですが、上記のような数式で表現されています。 $H[p]$ を解釈するにあたっては、確率分布 $p$ に対する汎関数(functional; 関数を入力とする関数)であることも把握しておくと良いです。また、基礎知識として汎関数に対する結果の最適化(最小化 or 最大化)を変分法(calculus of variations)と呼んでいることは抑えておくと良いと思います。また、エントロピーは $ln p(x_{i})$ の期待値(expectation)になっていることも抑えておくと良いと思います。

さて、数式だけで確認するとわかりづらいので、実際にPython実装を元に確認してみましょう。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(0,1,0.1)
p_x = np.tile(1.0/x.shape[0], 10)

print(x)
print(p_x)
plt.plot(x,p_x)
plt.show()

上記では1から10までにおける一様分布です。"p_x"の値が全て正かつ和が1であるので、確率分布の条件を満たしていることが確認できると思います。

f:id:lib-arts:20201022174742p:plain

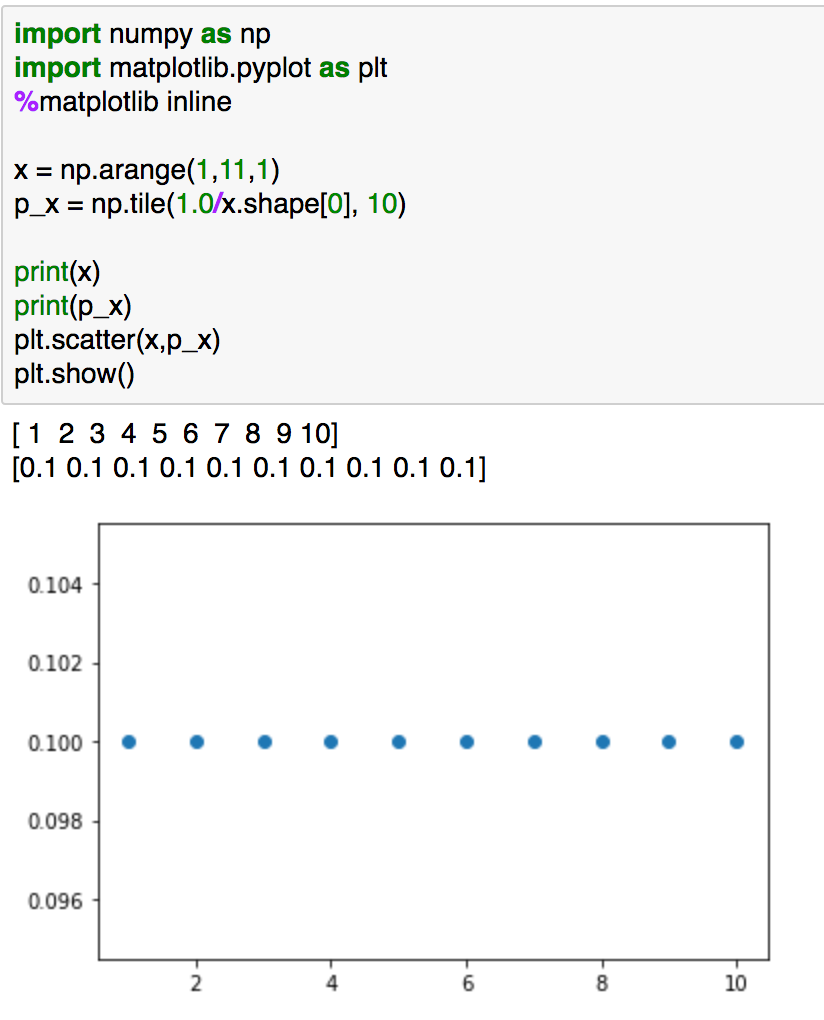
実行結果は上記になります。こちらのエントロピーについて計算します。

each_calc = p_x * np.log(p_x)

print(each_calc)
print(-np.sum(each_calc))

ここでのエントロピーの数式は $\displaystyle \sum_{i=1}^{10}x_{i} \ln p(x_{i})$ となるので、実装は"p_x * np.log(p_x)"で計算した"each_calc"の和にマイナスをつけたものになります。実行結果は下記のようになります。

f:id:lib-arts:20201022174833p:plain

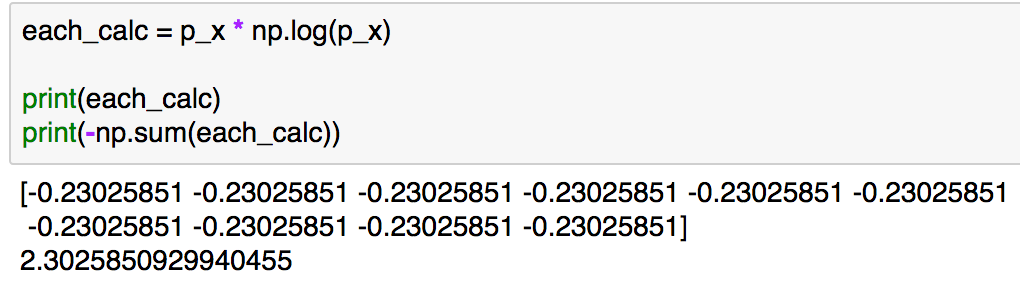
エントロピーの計算結果としては2.30...となります。

f:id:lib-arts:20201022175036p:plain

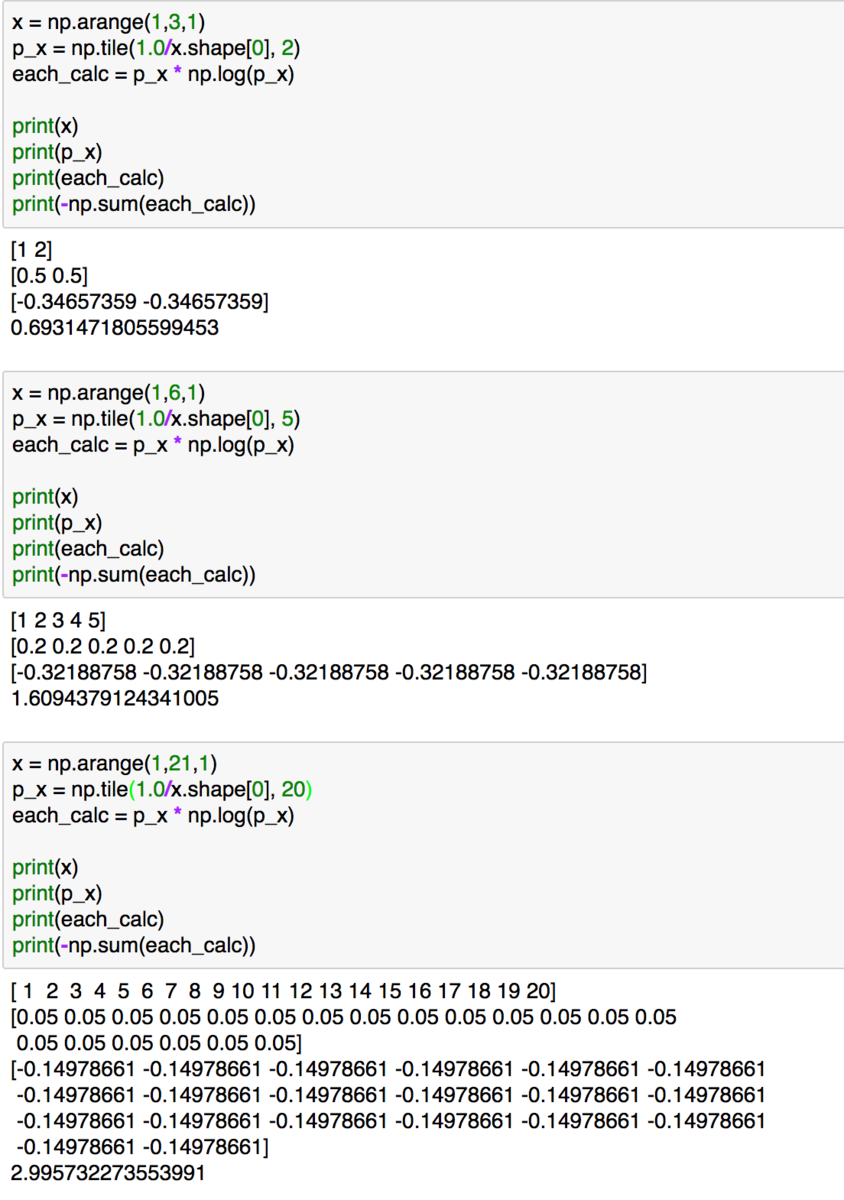
値のイメージがつきやすいように同様の計算をxの数を変えて行ってみると上記のようになります。xの数が大きくなるとエントロピーも増大していることが確認できます。

ここまでは離散的に考えていましたが、連続的にも考えてみましょう。

f:id:lib-arts:20201022184030p:plain

f:id:lib-arts:20201022184044p:plain

(1.103)の左辺の極限の中身の数式を用いて計算を行ってみます。（議論の簡易化のため、 $xlogx$ のx->+0の極限は0であることは既知とします。）

x = np.arange(0.1,10.1,0.1)
p_x = np.tile(1.0/10, 100)
each_calc = (p_x/10.) * np.log(p_x)

print(each_calc)
print(-np.sum(each_calc))

上記の実行結果は下記のようになります。

f:id:lib-arts:20201022184142p:plain

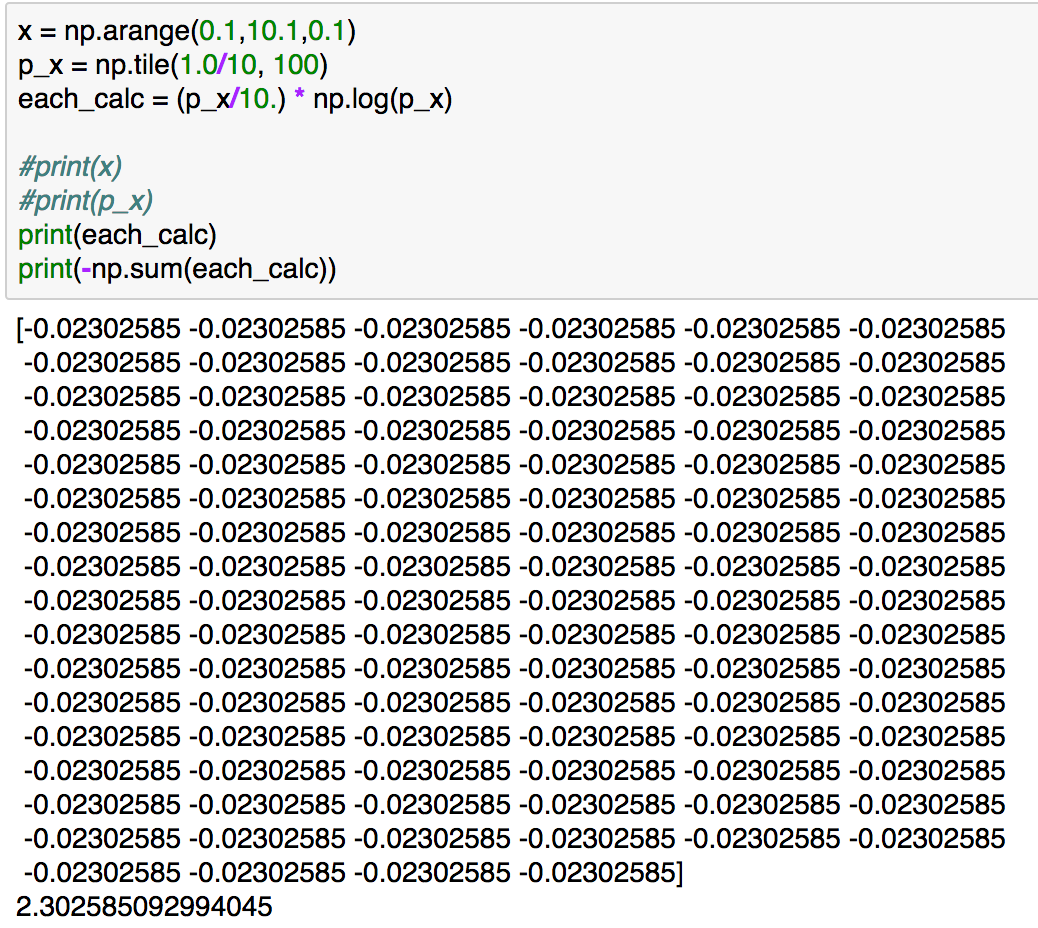
一番最初の計算例と結果が一致していることが確認できますが、同じ連続型の確率分布の区間を変えて計算を行ったと考えることもできるため、区間の取り方を変えてもエントロピーの値は基本的に変わらないというのがイメージできたかと思います。さて、(1.103)の数式ですが、区間の $\Delta$ を限りなく0に近づけることで、積分として取り扱っています。

1節では離散的な確率分布におけるエントロピーの計算における数式定義の取り扱いや、(1.103)の数式において、 $\Delta$ を0に限りなく近づけることで連続的な確率分布におけるエントロピーの計算が行えることを確認しました。2節ではこのエントロピーの数式を元にKLダイバージェンスについて確認していきます。

2. KLダイバージェンスについて
2節ではKLダイバージェンスについて確認していきます。が、1節における連続型確率分布におけるエントロピーをもう少し数式的に理解しておく方が望ましいので、先にエントロピーについてもう少し確認を行います。

f:id:lib-arts:20201022185616p:plain

まず、連続型確率分布におけるエントロピーの定義ですが、(1.104)のように行っています。ベクトル $\mathbf{x}$ について取り扱っていますが、基本的には(1.103)の式がベクトルの各要素毎に成立すると考えておけば十分だと思います。

f:id:lib-arts:20201022190026p:plain

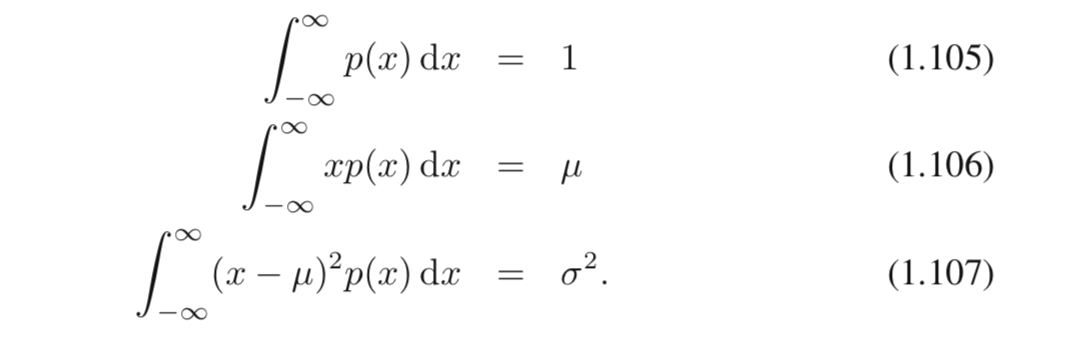
次に、エントロピーにおける三つの制約条件(constraint)について確認しますが、上記の(1.105)〜(1.107)として記載されています。(1.105)は確率分布の定義として、区間における積分が1になることを表しています。(1.106)と(1.107)は平均と分散の定義に対して、確率的な解釈を加えたものくらいに把握しておけば十分だと思います。

f:id:lib-arts:20201022190745p:plain
KLダイバージェンス(相互エントロピー; relative entropy)の記載については上記で理解しておくのが良さそうです。パターン認識(pattern recognition)の文脈でエントロピーを取り扱うにあたって、「未知の分布 $p(x)$ を近似の分布の $q(x)$ で取り扱うことを考える」というのがベースになると把握しておけば良いと思います。また、この時の指標として、(1.113)のような $KL(p||q)$ を導入したと考えれば良いと思います。KLダイバージェンスは確率分布の $p(x)$ を $q(x)$ で近似するにあたって、それぞれの類似度を計算する指標くらいに理解しておけば十分だと思います。

さて、数式だけを見ていても難しいので、実際に実装で確認してみます。

from scipy.stats import norm

x = np.arange(-10,10.1,0.1)
p_x_1 = norm.pdf(x, loc=0, scale=1)
p_x_1_5 = norm.pdf(x, loc=0, scale=1.5)
p_x_2 = norm.pdf(x, loc=0, scale=2)
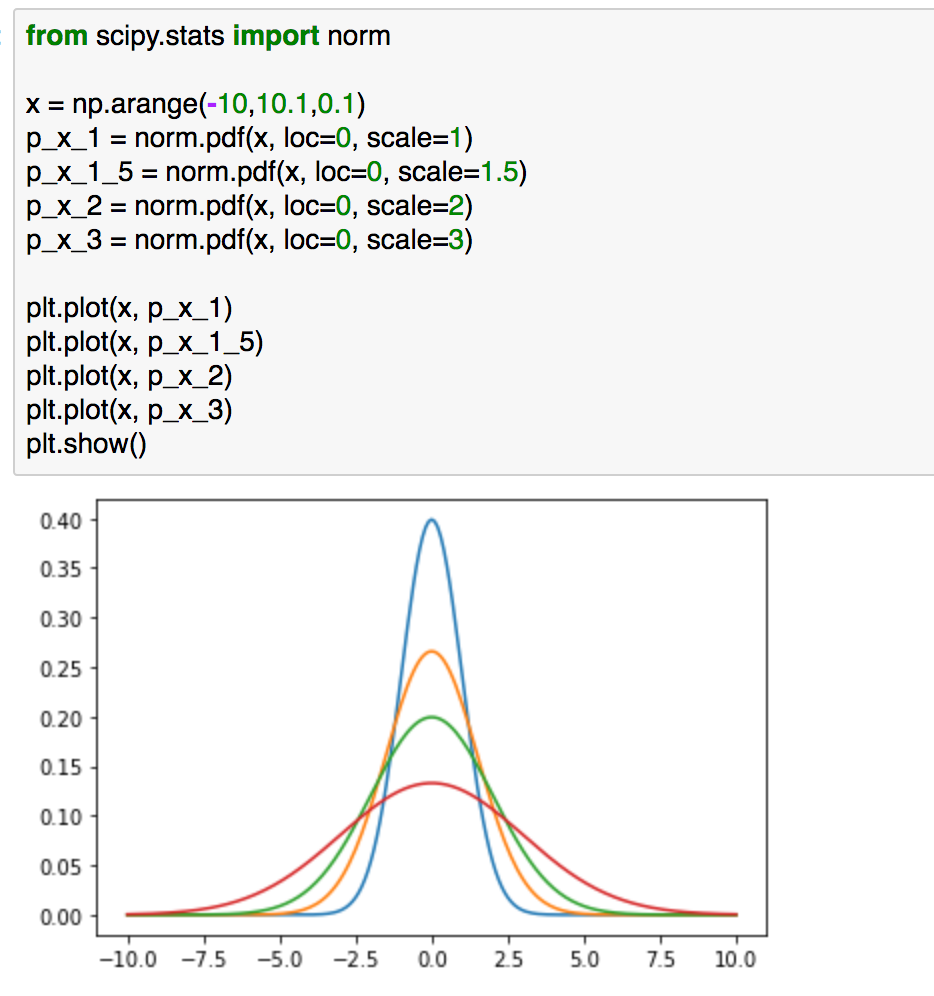
p_x_3 = norm.pdf(x, loc=0, scale=3)

plt.plot(x, p_x_1)
plt.plot(x, p_x_1_5)
plt.plot(x, p_x_2)
plt.plot(x, p_x_3)
plt.show()

f:id:lib-arts:20201022200517p:plain

まずは問題設定として、上記を考えるとします。上記の4つの確率分布において、青の確率分布と近しい確率分布はどれかを考えるにあたってKLダイバージェンスを計算するとします。

KLダイバージェンスの計算は下記のように実装できます。

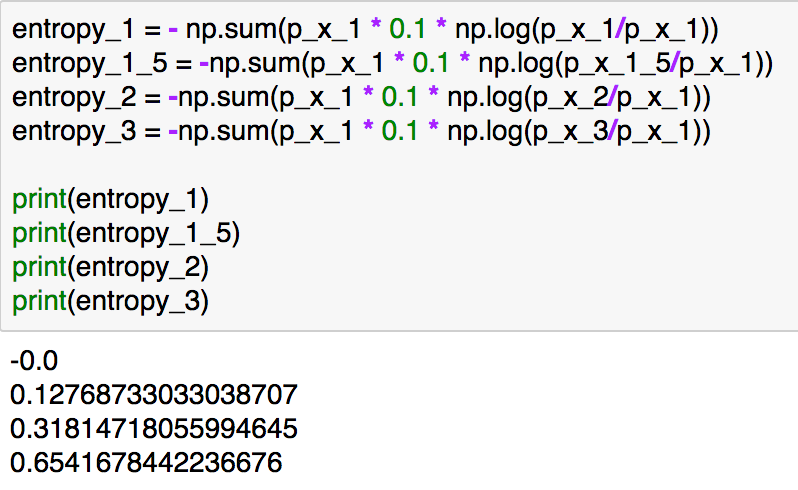
entropy_1 = - np.sum(p_x_1 * 0.1 * np.log(p_x_1/p_x_1))
entropy_1_5 = -np.sum(p_x_1 * 0.1 * np.log(p_x_1_5/p_x_1))
entropy_2 = -np.sum(p_x_1 * 0.1 * np.log(p_x_2/p_x_1))
entropy_3 = -np.sum(p_x_1 * 0.1 * np.log(p_x_3/p_x_1))

print(entropy_1)
print(entropy_1_5)
print(entropy_2)
print(entropy_3)

f:id:lib-arts:20201022201547p:plain
実行結果は上記のようになります。分散の値が同じ分布ではKLダイバージェンスは0、近い分布では値が小さく、分散の値が大きくなるにしたがってKLダイバージェンスの値は大きくなっています。（-10より小さい区間や10より大きい区間を取り扱わないなど、簡易化のためいくつか近似を行っていますが、概要を掴むのが目的のため細かいところの厳密性はここでは無視してください。）

3. まとめ
#1ではエントロピーとKLダイバージェンスの数式の確認や実装などを行いました。KLダイバージェンスは「確率分布を簡単な分布で近似するにあたって導入する、確率分布の類似度」とざっくり把握しておくと良いかと思います。
#2ではイェンセンの不等式と凸関数について考えつつ、KLダイバージェンスについて考察してみようと思います。

2020-10-18

リベラルの「新自由主義」・「格差社会」批判が支持を得られない理由｜マクロ経済を考える #3

economy Politics Society

f:id:lib-arts:20201018190435p:plain
昨今、「新自由主義」・「格差社会」への批判が話題になります。実体経済のデフレと金融商材のバブルが同時に起きているところや、それに伴い「格差」や「貧困」の問題が生じていると言われています。
いわゆる「リベラル」層はこれにあたって「新自由主義」や「格差社会」について批判し、いわゆる「保守」層はこれに反対します。ここまでの話はあくまで一般論として論じられている内容だと思いますが、あえて「いわゆる」をつけました。というのも、「リベラル」と「保守」の定義はややこしいからです。とはいえ、改めて定義し直すとさらにややこしくなりそうなので、「リベラル」と「保守」という形でクオテーションをつけることにより、一般的に使われている使い方を踏襲したまでであるということを強調しようと思います。

さて、この記事の本題ですが、「リベラルの新自由主義・格差社会の批判がなぜ支持を得られないか」です。もちろん支持者はいますが、ある程度「保守」側の方が優勢なのは数字を見ればわかると思います。とはいえ、ここで生じている面白いパラドックスが、「実はリベラルを支持する方がプラスになる人が保守を支持しているケースが多い」ということです。

以下、このパラドックスについて考察していきたいと思います。「新自由主義・格差社会批判は問題の一面だけを切り取っているに過ぎないので、支持されにくい」というのが結論ですが、これだけだとよくわからないと思うので詳細について論じていきます。
目次は下記になります。
1. 「新自由主義」について確認
2. なぜ「リベラル」は支持を得られないのか
3. 「新自由主義」が機能しなくなるリスクはどこにあるのか
4. 「機会平等」を論じる意義
5. まとめ

1. 「新自由主義」について確認
1節では「新自由主義」について簡単に確認したいと思います。Wikipediaの記載では「1930年以降、社会的市場経済に対して個人の自由や市場原理を再評価し、政府による個人や市場への介入は最低限とすべきと提唱する。1970年以降の日本では主にこの意味で使用される場合が多い」とされる、ネオリベラリズムについてを「新自由主義」と考えて異論は出ないかと思います(https://ja.wikipedia.org/wiki/新自由主義)。

重要なポイントを抜粋して確認してみます。

・個人の自由や市場原理の再評価
・政府による個人や市場への介入は最低限とすべきと提唱

抜き出すなら上記などが重要な点となるかと思います。

・民営化
・市場原理
・自己責任(自助・共助・自助そして自助)
・構造改革
・規制緩和

関連でよく使われるキーワードとしては上記などが挙げられると思います。

「民営化」によって「市場原理」に任せることで効率化を達成できる一方で、「自己責任」的な考えに基づいて競争することで「格差社会」や「貧困」を生み出しやすいとされています。

1節はあくまで一般論の再確認が目的だったのでここまでとします。(ここまでは一般論をまとめたに過ぎないので、ここまでは異論が出ないと思います。)

2. なぜ「リベラル」は支持を得られないのか
1節では「新自由主義」について確認をしましたが、2節ではなぜ「リベラル」の「新自由主義」批判は(潜在的支持者が多いのにも関わらず)支持を得られないのかについて考えたいと思います。

理由としては、「新自由主義」や「格差社会」そのものをいけないとしてしまうところにあるのではないかと思います。「新自由主義」や「格差社会」の良し悪しを論じがちですが、問題は「良し悪し」ではなく「機能する範囲か機能しない範囲か」や「許容できる範囲か許容できないか」を本来論じるべきです。

抽象的な話が続いたので、少し具体的にしてみます。たとえば「格差」一つ取っても、「家の広さが違うこと」と、「食事すらできない可能性があること」はどちらも「格差問題」かもしれませんが、程度問題としては大きく異なってくると思います。憲法に生存権があるように、この辺は関連で法律などが整備されていると思います。

「リベラル」が支持を得られづらいのは、本来「程度問題」であるべきものを、過度に「平等の問題」にすり替えてしまうというところにあると思います。もちろん、世の中が平和であるうちは良いのですが、基本的には二大政党制が求められる昨今です、「結果平等」を政策の基本においては多数の支持など得られるわけはありません。

それでは「リベラル」はどうすべきなのでしょうか。3節では現在の「保守」側の主張におけるリスクについて指摘し、論じてみようと思います。

3. 「新自由主義」が機能しなくなるリスクはどこにあるのか
3節では「新自由主義」のリスクについて論じてみようと思います。「モラルハザードによる不自由化」が「新自由主義」のリスクだと思います。
「自由主義」が「不自由」を生み出すというのはどういうことでしょうか。これについてはレントシーキングという言葉が面白いです。

Wikipediaの記載によるとレントシーキングは「民間企業などが政府や官僚組織へ働きかけを行い、法制度や政治政策の変更を行うことで、自らに都合よく規制を設定したり、または都合よく規制の緩和をさせるなどして、超過利潤（レント）を得るための活動を指す」とされています(https://ja.wikipedia.org/wiki/レントシーキング)。

ということは、「新自由主義」は「政治の経済への不介入」だけでなく、「経済の政治への介入」すらも生み出す可能性があるということです。「賄賂」、「利権」、「利益誘導」などの問題はここに起因します。「ルールを無くして自由に競争しよう」というのが「新自由主義」だったはずが、「ルールを作って儲けよう」にだんだんと変わってきます。「政治家への賄賂」で話題になるのは数十万〜数千万くらいの場合が多いのですが、この程度の金額で国益や国民の利益を売り渡されるという事態にもなりかねません。

レントシーキングやそれに伴う民営化については別途論じようと思います。本題に戻って、「新自由主義」が機能しなくなるリスクとしては「モラルハザード」が起きる可能性です。これを防ぐにはどうしたら良いのでしょう。続く4節で防ぐにあたっての「機会平等」を実現する社会について論じてみます。

4. 「機会平等」を論じる意義
3節では「新自由主義」がモラルハザードを引き起こす可能性について論じてきましたが、4節ではそれを受けて「機会平等」について考えていければと思います。Wikipediaでは機会平等(機会均等; Equal opportunity)は「全ての人々が同様に扱われるべきであるという観念で、特に人為的な障壁・先入観・嗜好などを「明らかに合理的と見なされているもの」以外全て取り除くべきである」とされています(https://ja.wikipedia.org/wiki/機会均等)。

機会平等についての解説で下記も重要であると思われたので抜粋しておきます。

・重要な仕事は『最も優秀な者』にゆだねられるべきだという考えに基づく考え方
・選定プロセスから恣意性を排除し、事前に合意を経た公平性に基づく、個々の専門性に関連した評価過程を元にした手続き・法的理念を重要視する

この「機会平等」という考え方は「リベラル」が論じがちな「結果平等」とは異なり、社会主義的な経済に現れがちな停滞にはなりづらいことから比較的支持されやすいかと思います。

5. まとめ
今回は「リベラル」の「新自由主義」や「格差社会」批判が支持を得られない理由について考察してきましたが、「結果平等」は多数の支持は得られづらいのではという点を指摘しました。おそらく「結果平等」を求めている人は世の中それほど多くはいないのではないかと思います。

一方で、行き過ぎた「新自由主義」は結局はレントシーキングを引き起こし、だんだんと「不自由」な世の中を構成していくリスクがあります。とはいえある程度現状が「自由な社会を実現する過程」に見えている可能性があります。が、昨今の入試改革の話などを見る限り、「機会平等」というよりは「階級固定」的な方向に向いているように見えます。保守は元々「前例を大事にする」考え方なのである程度「階級固定」的な話は仕方がないのかもしれません。（というよりは「新自由主義」的な考え方は本来の意味での保守にはなじまないのだと思います。）

結論としては「リベラル」は「競争社会の否定」ではなく、「機会平等に基づく競争社会を肯定する一方でそこから外れた際の支援を重視すべき」ではないかということです。「保守」と「リベラル」については関連する文脈が多すぎるので改めて別途論じられればと思いますが、少なくとも「結果平等」を重視するだけが「リベラル」ではないのでは、というのを再考する必要はあると思います。