EMアルゴリズムの論理構成の全体像|Python実装で理解する変分推論(VariationalInference) #4

当シリーズはPython実装を通して変分推論を理解していこうということで進めています。下記などを主に参照しています。
Pattern Recognition and Machine Learning | Christopher Bishop | Springer
#3では変分推論の枠組みにおけるEMアルゴリズムを混合正規分布(Gaussian Mixture Models)を題材にしながら確認しました。
#3の論理展開が若干わかりづらいとも思われたため、#4ではEMアルゴリズムの論理構成の全体像について再度確認を行えればと思います。
以下、目次になります。
1. EMアルゴリズムの全体像まとめ
2. 変分推論への展開
3. まとめ
1. EMアルゴリズムの全体像まとめ
1節ではEMアルゴリズムの全体像のまとめについて行えればと思います。まず抑えておきたいのが正規混合分布(Gaussian Mixture)における、各正規分布の平均()と分散(
)、そして混合させるにあたってのそれぞれの割合(
)のパラメータを推定するという問題設定です。

EMアルゴリズムは、上記における(9.14)式や(9.36)式のようなそれぞれのパラメータに関する尤度(Likelihood)の最適化のアルゴリズムであり、基本的には微分などを用いたアプローチによりパラメータの推定を行います。通常の流れでの正規混合分布における尤度は(9.14)式のようになるのですが、の中に
があるためこの式は少々取り扱いづらく、(9.14)を起点に(9.24)〜(9.27)の導出を行うのはなかなか大変です((9.14)から(9.24)のベースになる(9.16)式の導出の計算が1行で済んでいるのですが、目の錯覚ということでポジティブに解釈しましょう)。

さて、(9.14)式のようにだけを元に尤度を取り扱うと計算が複雑になるので、それぞれのサンプルにおける分布の配分に関係する
も導入し、
と同様に考えることで尤度の式が(9.36)式のように尤度の式をシンプルに変更しています。が、ここで
については観測の
とパラメータの
がわかっている状況での事後分布としてしか表現できないため(Zは観測できない)、(9.40)式のように尤度の期待値を考えるということをします。(9.14)式、(9.40)式のどちらにおいても
の事後分布である負担率(
; responsibility)を固定した上でそれぞれのパラメータに関して最適化を行えば、(9.24)〜(9.27)を導出することができます。

負担率については上記で示した(9.13)式で表されています。要は観測値のがある上で、各分布のパラメータを固定すれば得られるということで、K-meansにたとえるなら各クラスタの平均ベクトルに基づいてサンプルの割り当てを決めるのと同様な操作を行います(ここがEステップに相当します)。
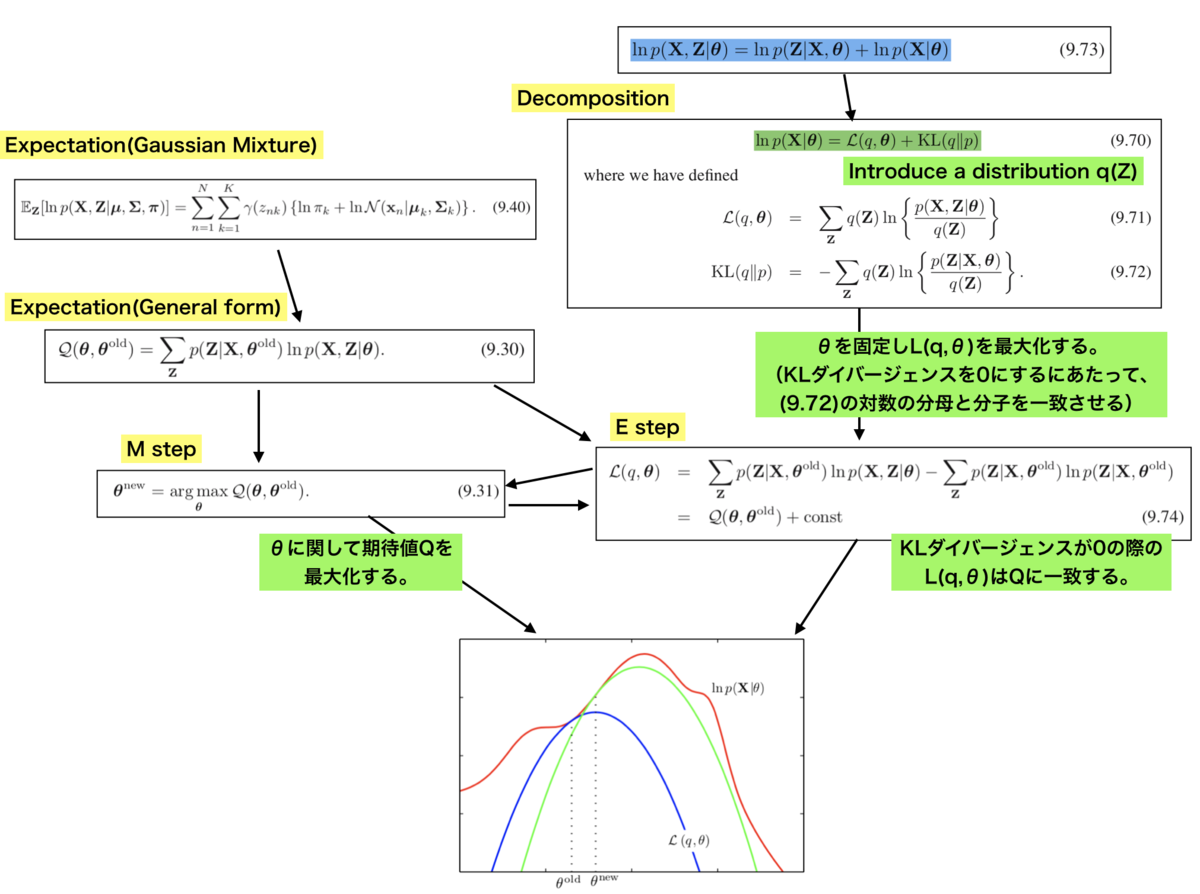
また、対数尤度の期待値については正規混合分布における(9.40)式から、一般的な式として上記の(9.30)式のように書き直すことができます。が(9.13)式の負担率の定義と対応しています。この(9.30)式において
に関して最適化を行っているのが(9.31)式で示したMステップです。
また、ここでの議論を解釈するにあたって確率分布のを導入し、(9.70)式のような分解を行っています。(9.70)式については(9.71)式〜(9.73)式を用いることで導出が可能です。ここで重要なのが、(9.70)式において
を最大化するにあたってKLダイバージェンスを0にする条件として、
を導出し、これを(9.71)に代入した結果として(9.74)式が得られるということです。これがEステップに相当するのですが、(9.74)式と(9.31)式の繰り返しとして全体のアルゴリズムを見ることにより、図におけるEMアルゴリズムの解釈が導出できます。Eステップでは
の値を固定して
をアップデートしていくため、青を緑に移動させるようなイメージです。また、Mステップでは
を最大化する
を導出します。
2. 変分推論への展開
2節ではここまでのEMアルゴリズムに関する議論をベースに、変分推論への展開を確認します。

上記のように、変分推論では(9.70)式で導入したに関しての取り扱いを考えていきます。(9.70)〜(9.72)を(10.2)〜(10.4)のように書き直して、
について議論を行っています。考え方としてメジャーなものとして、(10.5)のように
を積の形に分解したmean-field的な考え方が紹介されています。
変分推論に関して詳しくは#5以降で取り扱うとして、今回はここまでとします。
3. まとめ
#4ではEMアルゴリズムの全体像について再度まとめながら変分推論への展開について簡単に確認しました。
#5以降では引き続き、変分推論について確認していければと思います。