分散共分散行列の固有値問題と主成分分析(PCA)|スクラッチ実装で理解する機械学習アルゴリズム #1

データ分析や機械学習を行う上で、必ずしも全ては必要ないにしても最低限の理論の理解は欠かせません。とはいえ、とっつきづらかったり数学がネックになったりで学習に挫折するケースをよく拝見します。
こういった挫折のケースの要因は読み手の知識不足の際もあるのですが、本によっては説明が不十分だったり読みにくかったり誤植があったりと単に理解しやすい文面で書かれていないというのもあります。また、実装本の中にはライブラリの使い方の説明がメインのケースもあります。
そこで、本シリーズではあえてスクラッチ実装を元に機械学習のアルゴリズムを実装していくことで、アルゴリズムの概要を掴んだり理論の流れを掴んだりできるようにできればと思います。実装のほとんどが車輪の再発明に近くなりますが、ベーシックなアルゴリズムをあえて一から自分で追ってみるというのは引き出しを増やすという意味で非常に有意義です。
#1では主成分分析について実装を通して理解を深めていければと思います。以下目次になります。
1. 主成分分析とは、分散最大化による定式化
2. 分散共分散行列と固有値・固有ベクトル
3. 実装で理解するPCA
4. まとめ
1. 主成分分析とは、分散最大化による定式化
主成分分析(PCA; Principal Component Analysis)は、次元削減、非可逆データ圧縮、特徴抽出、データの可視化などに広く適用される手法です。主成分分析を定義するにあたっては二つの異なる方法がありますが、両者とも同じアルゴリズムを与えるとされているので、当座のところはメジャーな分散最大化による定式化だけ知っておけば十分だと思われます。先に結論だけ述べておくと、分散共分散行列の最大固有値に対応する固有ベクトルを主成分と考えるのが主成分分析です。以下の定式化の話は初学の際は難しいと思いますので、余裕がなければ飛ばしていただけたらと思います。
分散最大化にあたっての定式化は、ある軸に射影されたデータの分散を最大化するように考えます。まず、射影されたデータの分散を下記のように与えます。
ここでSはデータの分散共分散行列です。この分散の最大化にあたって制約条件としてを課した際にラグランジュの未定乗数法を用いて
に関する微分を0とおくと、
が導出できます。これはuがSの固有ベクトルとならねばならないことを述べています。また、左からをかけて
を用いると、
となるので、分散は
を最大固有値
に対応するように選んだ時に最大となり、この際の固有ベクトルは第一主成分と呼ばれます。
最低限の理解にあたって必要だと思われる内容については説明を行いましたが、主成分分析の詳細については「パターン認識と機械学習 下(C・M・ビショップ)」の12章が詳しいので、詳しく知りたい方はそちらを参照ください。(数式の説明は12.1.1から抜粋しました)
パターン認識と機械学習 下 - 丸善出版 理工・医学・人文社会科学の専門書出版社
2. 例題における分散共分散行列
1節で主成分を求めるにあたっては分散共分散行列の最大固有値に対応する固有ベクトルを求めれば良いということがわかりました。とはいえ、1節の論理展開は抽象的で難しいので、2節では具体的な例題を用いて話を進めていければと思います。
import numpy as np
import matplotlib.pyplot as pltnp.random.seed(87655678)
x = (np.random.rand(100)-0.5)*2
y_1 = x
y_2 = x + (np.random.rand(100)-0.5)*0.4
y_3 = (np.random.rand(100)-0.5)*2plt.subplot(221)
plt.scatter(x,y_1)
plt.subplot(222)
plt.scatter(x,y_2)
plt.subplot(223)
plt.scatter(x,y_3)
plt.show()
解説にあたっては上記の実行結果を元に話を進めます。実行結果は下図になります。

3つのデータセットを生成しており、y_1はxと同じ値、y_2はxの値にノイズを加えたもの、y_3は無相関で生成したものになります。また、分散共分散行列は下記のように求めることができます。
Sigma_x_y_1 = np.cov(x,y_1)
Sigma_x_y_2 = np.cov(x,y_2)
Sigma_x_y_3 = np.cov(x,y_3)
print(Sigma_x_y_1)
print(Sigma_x_y_2)
print(Sigma_x_y_3)
実行結果は以下になります。

3. 実装で理解するPCA(分散共分散行列の固有値、固有ベクトルを求める)
2節で求めた分散共分散行列の最大固有値に対応する固有ベクトルを求めることで、第一主成分を抽出できます。
la_1, v_1 = linalg.eig(Sigma_x_y_1)
la_2, v_2 = linalg.eig(Sigma_x_y_2)
la_3, v_3 = linalg.eig(Sigma_x_y_3)slope1 = v_1[0,0]/v_1[1,0]
slope2 = v_2[0,1]/v_2[1,1]
slope3 = v_3[0,1]/v_3[1,1]
slope1_ = v_1[0,1]/v_1[1,1]
slope2_ = v_2[0,0]/v_2[1,0]
slope3_ = v_3[0,0]/v_3[1,0]plt.grid()
plt.subplot(221)
plt.scatter(x,y_1)
plt.plot(x,slope1*(x-np.mean(x)),color='red')
plt.plot(x,slope1_*(x-np.mean(x)),color='green')
plt.subplot(222)
plt.scatter(x,y_2)
plt.plot(x,slope2*(x-np.mean(x)),color='red')
plt.plot(x,slope2_*(x-np.mean(x)),color='green')
plt.subplot(223)
plt.scatter(x,y_3)
plt.plot(x,slope3*(x-np.mean(x)),color='red')
plt.plot(x,slope3_*(x-np.mean(x)),color='green')
plt.show()
実行結果は以下のようになります。
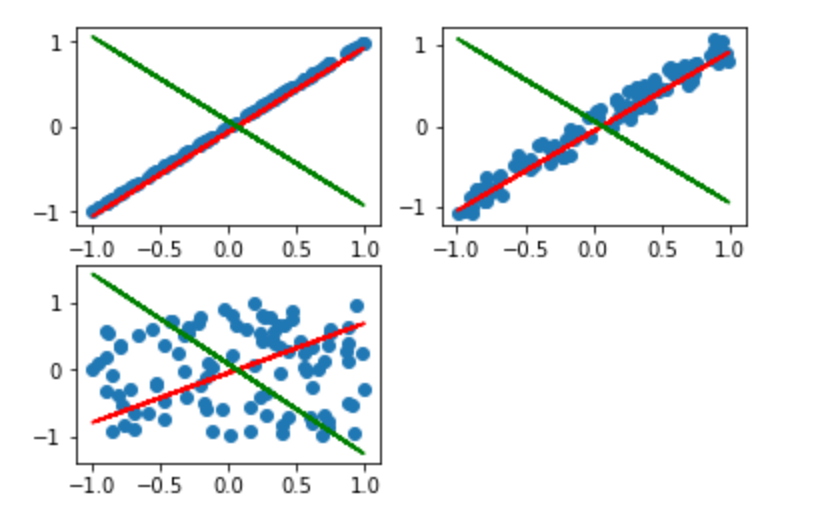
赤が第一主成分、緑が第二主成分になります。
4. まとめ
#1では1節で主成分分析の概要と分散最大化による導出、2節で例題における分散共分散行列、3節では主成分の計算と図式化を行いました。このように実際に実装しながら見ることによって、イメージが掴みやすくなったのではと思います。