類題を用いた行列の計算とMLPの推論の問題演習｜高校数学の演習を通して理解するニューラルネットワーク #9

f:id:lib-arts:20190527195235p:plain

当連載は、高校数学の演習を通して機械学習のアルゴリズムの一つであるニューラルネットワークを理解しようというものです。連載の経緯につきましては#1にまとめましたので下記をご覧ください。

関数・微分の演習と解説｜高校数学の演習を通して理解するニューラルネットワーク #1 - lib-arts’s diary
#1~#6では6題の例題の解説とそれをベースにした回帰分析の学習の流れとモデルの数式のMLPやCNNへの拡張について取り扱いました。

畳み込みネットワーク(CNN)へのモデルの拡張｜高校数学の演習を通して理解するニューラルネットワーク #6 - lib-arts’s diary
#6までで解説的な話題は一通り取り扱えたと思いますが例題だけだとしっくりこないと思いますので、#7以降では問題演習について取り扱っています。(#7では関数と微分について、#8では最小値問題や最適化について取り扱いました。）

#9では行列の計算とMLPの推論について問題演習として取り扱います。

Math Exercises
以前セミナーを行った際に上記のサポートページを作っていただいたので、こちらから何題か抜粋しつつ足りないところは改めて作成できればと思います。
以下、目次になります。

1. 行列の計算に関する問題演習
2. MLPの推論に関する問題演習
3. まとめ

1. 行列の計算に関する問題演習

https://kenchaaan.github.io/exercises_math/exercises/exercise1.html (Exercise 1)
より、1,2,5,8,10を取り扱えればと思います。

問題. 以下の行列の積の計算を行え。
Q.15 $\left(\begin{array}{rr}2　-1\\3　　1\\\end{array}\right)$ $\left(\begin{array}{rr}-3　　2\\4　-1\\\end{array}\right)$
Q.16 $\left(\begin{array}{rr}4　　0\\9　-5\\\end{array}\right)$ $\left(\begin{array}{rr}-5　　6\\3　-9\\\end{array}\right)$
Q.17 $\left(\begin{array}{rr}w_{11}　w_{12}\\w_{21}　w_{22}\\\end{array}\right)$ $\left(\begin{array}{rr}x\\y\\\end{array}\right)$

解答.
A.15
$\left(\begin{array}{rr}2　-1\\3　　1\\\end{array}\right)\left(\begin{array}{rr}-3　　2\\4　-1\\\end{array}\right)=\left(\begin{array}{rr}-6-4　4+1\\-9+4　　6-1\\\end{array}\right)=\left(\begin{array}{rr}-10　5\\-5　　5\\\end{array}\right)$

A.16

$\left(\begin{array}{rr}4　　0\\9　-5\\\end{array}\right)\left(\begin{array}{rr}-5　　6\\3　-9\\\end{array}\right)=\left(\begin{array}{rr}-20+0　　24+0\\-45-15　54+45\\\end{array}\right)=\left(\begin{array}{rr}-20　24\\-60　99\\\end{array}\right)$

A.17

$\left(\begin{array}{rr}w_{11}　w_{12}\\w_{21}　w_{22}\\\end{array}\right)\left(\begin{array}{rr}x\\y\\\end{array}\right)=\left(\begin{array}{rr}w_{11}x+w_{12}y\\w_{21}x+w_{22}y\\\end{array}\right)$

解説.
行列の積の計算については慣れるしかないので、数をこなして手が勝手に動くようにすると良いと思います。
ニューラルネットワークに限らず、機械学習の様々なアルゴリズムは行列の計算をベースにしています。それどころか理工系のだいたいの分野は行列や線形代数の簡単な知識を必要とするので、慣れるまで取り組んでも損はない内容です。

https://kenchaaan.github.io/exercises_math/exercises/exercise1.html
上記のページでは10題演習問題があるので、1節で取り扱った3題の演習でまだしっくりきていない方は上記のページで演習していただけたらと思います。

2. MLPの推論に関する問題演習

https://kenchaaan.github.io/exercises_math/answers/answer6.html (Exercise 6)
より、1,2,4を取り扱えればと思います。

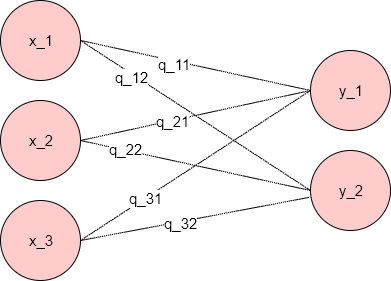
問題. 以下の図を行列の積を用いて表せ。注 ... "x_a"は $x_{a}$ を表している(例: x_0 => $x_{0}$ 、q_12 → $q_{12}$ )
Q.18

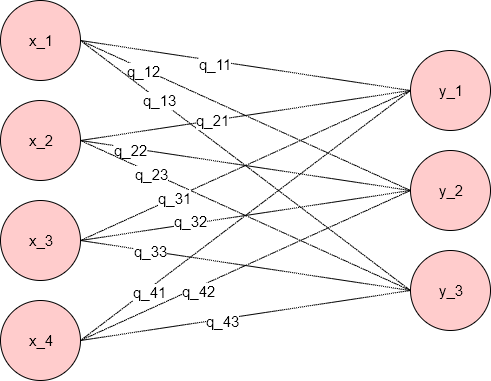
Q.19

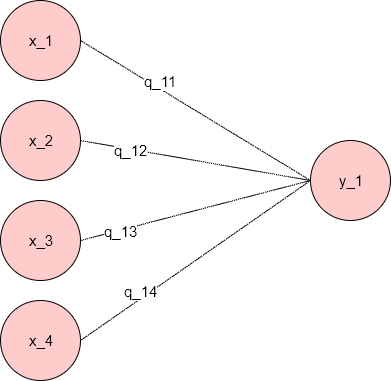
Q.20

解答.
A.18

$\left(\begin{array}{rr}q_{11}　q_{21}　q_{31}\\q_{12}　q_{22}　q_{32}\\\end{array}\right)\left(\begin{array}{rrr}x_{1}\\x_{2}\\x_{3}\\\end{array}\right)=\left(\begin{array}{rr}y_{1}\\y_{2}\\\end{array}\right)$
A.19

$\left(\begin{array}{rrr}q_{11}　q_{21}　q_{31}　q_{41}\\q_{12}　q_{22}　q_{32}　q_{42}\\q_{13}　q_{23}　q_{33}　q_{43}\\\end{array}\right)\left(\begin{array}{rrrr}x_{1}\\x_{2}\\x_{3}\\x_{4}\\\end{array}\right)=\left(\begin{array}{rrr}y_{1}\\y_{2}\\y_{3}\\\end{array}\right)$
A.20