最小値問題と最適化｜高校数学の演習を通して理解するニューラルネットワーク #2

f:id:lib-arts:20181228181633p:plain

当連載は、高校数学の演習を通して機械学習のアルゴリズムの一つであるニューラルネットワークを理解しようというものです。連載の経緯につきましては#1にまとめましたので下記をご覧ください。

簡単な6題の例題をもとにニューラルネットワークの仕組みに現れる基礎的な数学についてフォーカスします。
#1では関数と微分について取り扱いましたのsw、それを受けて#2では最小値問題と最適化について取り扱えればと思います。
以下、目次になります。

1. 例題③ 最小値問題
2. 例題④ 勾配降下法と等比数列（最適化）
3. まとめ

1. 例題③ 最小値問題

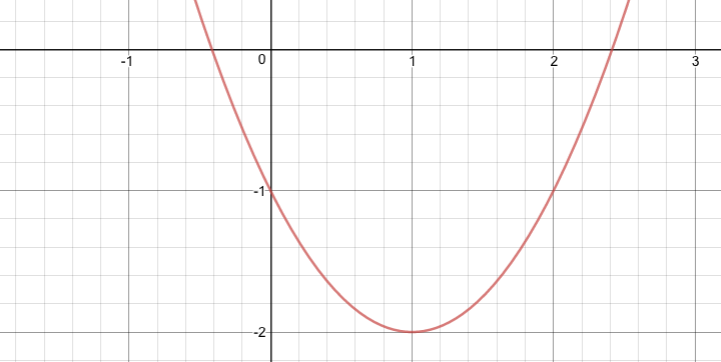
1節では最小値問題について取り扱います。二次関数の最小値問題なので、平方完成や微分など様々な単元で出てきた問題なのではないかと思います。ベーシックな問題ではあるのですが、ここでの理解が最適化と呼ばれるニューラルネットワークの学習の処理の理解の手助けとなります。

ex.03

$f(x) = x^2 + 2x + 3$ が最小値をとる際のxを導関数（微分）を用いて求めよ。

Answer.

与えられた関数が下に凸である二次関数のため、最小値を取る際に傾きの $f'(x) = 0$ となるので、

$f'(x) = 2x+2 = 0$

したがって $x = -1$

解説.

与えられた関数は下に凸な関数なので、 $f'(x)$ は単調増加します。このため、 $f'(x) = 0$ の点を境に $f(x)$ の値は減少から増加に変わります。この点で最小となります。

また、この問題には平方完成を用いた別解があるのですが、この後の話に繋がりやすいようにあえて微分で解いています。問題自体は二次関数の最小値問題と非常に簡単な問題なのですが、この問題の理解がex.04で解説する勾配降下法の理解に繋がってきます。

2. 例題④ 勾配降下法と等比数列（最適化）

上記の記事でも取り扱ったのですが、イメージをつかむのに秀逸なのでよく用いている問題です。ex.03の最小値問題は微分=0を解きましたが、それを行わなくても微分の値を用いて最小値を求めることができるというのをex.04を通して抑えていきます。

ex.04

$f(x)=x^2$ 、 $f'(x)=2x$ 、 $α=0.25$ 、 $x_{0}=2$ のとき、
${\large x_{n+1} = x_{n}-α f'(x_{n})}$ ・・(※)

を用いて、 $x_{1}$ 、 $x_{2}$ 、 $x_{n}$ 、 $\displaystyle \lim_{n \to \infty} x_{n}$ を求めよ。

Answer.

$x_{n+1} = x_{n}-0.25 × 2x_{n}$ ・・(1)

上記は(※)に $α=0.25$ 、 $f'(x_{n})=2x_{n}$ を代入したものになる。

$x_{n+1} = 0.5x_{n}$ ・・(2)

(1)を変形すると(2)のようになる。(2)は高校数学の数列で習う漸化式であり、n+1番目がn番目の0.5倍になっているので{ $x_{n}$ }は公比0.5の等比数列になる。そのため、数列の基本的な解き方に基づいて下記のように解いていくことができる。

$x_{1}=0.5×x_{0}=0.5×2=1$

$x_{2}=0.5×x_{1}=0.5×1=0.5$

$x_{n}=0.5×x_{n-1}=0.5^2×x_{n-2}=...=0.5^n×x_{0}=0.5^n×2$

$\displaystyle \lim_{n \to \infty} x_{n}$ = $\displaystyle \lim_{n \to \infty} 0.5^n×2=0$

それぞれが題意を満たす答えとなっている。

解説.

参照記事でも述べましたが、問題に出てきた(※)の式は実は勾配降下法の式です。ex.04ではこの勾配降下法の式を用いて最小値問題を解いています。 $\displaystyle \lim_{n \to \infty} x_{n}$ は実は $f(x)$ が最小値となる $x$ の値と一致します。（数値的な解を求めるにあたっての都合上極限は大きな値となるのでこれは近似解です）

また、なぜ勾配降下法を用いることで最小値を求めることができるかですが、こちらについては傾きの逆方向に動くと言うのがポイントです。傾きが負の際は正の向きに進むと $f(x)$ の値は小さくなるし、傾きが正の際は負の向きに進むと $f(x)$ の値が小さくなります。これに $α$ を学習率としてかけることで更新の度合いを制御します。

直感的な式の理解については上記のようにまとめています。

また、この勾配降下法の式ですが、ニューラルネットワークの学習時などによく用いられます。近年ではAdamと呼ばれるより複雑な最適化なども用いられていますが、ベースには勾配降下法の考え方があるため、ベースの原理さえつかんでおけば同様に理解することが可能です。

3. まとめ

#2の記事では二通りの方法で最小値問題を解く方法について解説しました。一つはex.03のように $f'(x)=0$ を解く方法、もう一つはex.04のように近似的な手法を用いて解く方法です。また、最適化という言葉が出てきましたが、ある目的関数(objective)を最小化(マイナスをつけるだけなので最大化も同義)する変数の値を求める問題を最適化問題と言います。最適化問題においてex.03のように厳密に解ける場合もありますが、多くのケースでそれが解けないケースも存在するのでex.04のように近似的な手法を用いて解くケースもあります。

詳しくは追々掴むとして、#2の段階では一旦上記のような最小値問題の二つの解き方を把握しておいていただければと思います。