確率分布を可視化する①（基本的な分布）｜Python実装で視覚的に理解するベイズ統計 #1

f:id:lib-arts:20190419173312p:plain

ベイズ統計は統計や機械学習の文脈ではややとっつきづらいトピックになるかと思います。TreeベースのアルゴリズムやDeep Learningなどの関数近似の方が理解しやすいかつ、最近のトレンドに占める割合が多い印象です。とはいえ、ベイズ統計の理論の枠組みで考察すると面白いことも多く、是非使いこなしたい考え方です。
ベイズ統計は入門書レベルで数式が多いこともあり挫折しがちなトピックでもあるのですが、当シリーズではそういった問題意識の下で、ベイズ統計の各コンポーネントをPythonを用いて実装し可視化を試みることで、ベイズ統計を視覚的に理解していこうと思います。読者想定としては、「ベイズの定理はわかるけど結局ベイズ統計が何なのかありがたみがわからない」、「事前分布を事後分布に更新するのはわかるけど、実際結果としてどうなるのかがわからない」というレベルを想定します。そのため、基本事項は原則として説明しませんが、基本事項を実装を用いて考察するなどは行う予定です。
#1ではまずは基本的な確率分布の可視化から行なっていきます。
以下目次になります。
1. 前提知識整理、参考本の紹介
2. 基本的な離散確率分布の可視化（二項分布、ポアソン分布）
3. 基本的な連続確率分布の可視化（正規分布、ガンマ関数、ベータ分布）
4. まとめ

1. 前提知識整理、参考本の紹介
1節では前提知識の整理と参考本の紹介を行えればと思います。まず、基礎統計（統計検定二級）レベルは基本的に既知として取り扱っていきますので、自信のない方は先に下記をご確認ください。

Pythonで実装する推測統計①（統計量）｜スクラッチ実装で理解する基礎統計 #4 - lib-arts’s diary

Pythonで実装する推測統計②（点推定、区間推定）｜スクラッチ実装で理解する基礎統計 #5 - lib-arts’s diary

Pythonで実装する推測統計③（統計的仮説検定）｜スクラッチ実装で理解する基礎統計 #6 - lib-arts’s diary

上記がわかれば大体わかると思いますが、所々説明は省略しますので説明不足の点やわかりづらい点などありましたら下記の書籍などを参考にしていただくと良いかと思います。
・データ解析のための統計モデリング入門

データ解析のための統計モデリング入門 - 岩波書店
通称緑本。ざっと眺めてとっかかりを掴むには良い本ですが、数式があまり出てこなかったり細部の記述がいい加減だったりで少々厳密性には欠けます。教科書というより入門にあたっての読み物としておすすめ。

・ベイズ推論による機械学習入門

ベイズ推論による機械学習入門機械学習スタートアップシリーズ | 書籍情報 | 株式会社講談社サイエンティフィク
コンパクトな一冊。入門者向けとありますがあくまでベイズの入門であって、統計や機械学習の視点で見るなら中級者向けだと思います。

・パターン認識と機械学習上（by C.M.ビショップ）

パターン認識と機械学習上 - 丸善出版理工・医学・人文社会科学の専門書出版社
言わずと知れたPRML。余裕のある際に挑戦するで十分だと思います。

2. 基本的な離散確率分布の可視化（二項分布、ポアソン分布）
2節では離散確率分布の中でも基本的な内容である、二項分布とポアソン分布について可視化を行います。
まず、二項分布(Binominal distribution)ですが、N回の試行において一回あたり確率 $\mu$ で観測される事象がk回観測される確率を表します。こちらを数式で表すと下記です。
$P(k|N,\mu)={}_N C_k \mu^k(1-\mu)^{N-k}$
下記を実行することで、N=50、p=0.3,0.5,0.8で二項分布を描くことができます。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom

k = np.arange(0,50,1)
p_1 = binom.pmf(k, 50, 0.3, loc=0)
p_2 = binom.pmf(k, 50, 0.5, loc=0)
p_3 = binom.pmf(k, 50, 0.8, loc=0)

plt.plot(k,p_1)
plt.plot(k,p_2, color="orange")
plt.plot(k,p_3, color="green")
plt.show()

実行結果は下記のようになります。実装にはscipy.statsを用いました。使用しているbinom.pmfのpmfは確率質量関数(probability mass function)のことで、確率密度関数の離散バージョンと捉えておくと良いです。

f:id:lib-arts:20190610155945p:plain

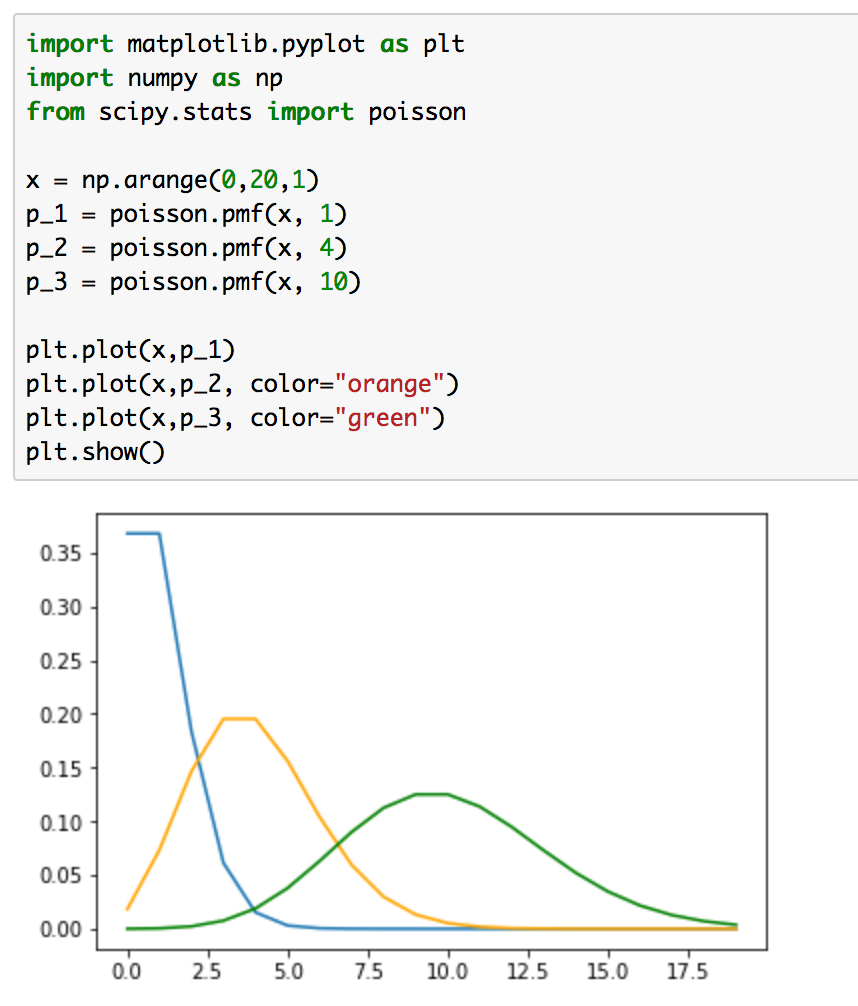
次にポアソン分布(Poisson distribution)について取り扱います。ポアソン分布を数式として表すと以下のようになります。
$P(x|\lambda)=\frac{\lambda^{x}e^{-\lambda}}{x!}$
下記を実行することで[\lambda=1,4,10]についてのポアソン分布を描くことができます。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import poisson

x = np.arange(0,20,1)
p_1 = poisson.pmf(x, 1)
p_2 = poisson.pmf(x, 4)
p_3 = poisson.pmf(x, 10)

plt.plot(x,p_1)
plt.plot(x,p_2, color="orange")
plt.plot(x,p_3, color="green")
plt.show()

実行結果は下記のようになります。こちらも実装にはscipy.statsを用いました。

f:id:lib-arts:20190610160027p:plain

3. 基本的な連続確率分布の可視化（正規分布、ガンマ関数、ベータ分布）
2節では離散確率分布について取り扱ったので、3節では連続確率分布について取り扱っていきます。
まずは様々なケースで用いられる正規分布に関してです。正規分布を数式で表すと下記のようになります。
$P(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(x-\mu)^2}{2\sigma^2})$
下記を実行することで、 $\mu=0,4$ 、 $\sigma^2=1,4$ について4つの正規分布を描くことができます。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

x = np.arange(-10,10,0.2)
p_1 = norm.pdf(x, 0, 1)
p_2 = norm.pdf(x, 0, 2)
p_3 = norm.pdf(x, 2, 1)
p_4 = norm.pdf(x, 2, 2)

plt.plot(x,p_1)
plt.plot(x,p_2, color="orange")
plt.plot(x,p_3, color="green")
plt.plot(x,p_4, color="red")
plt.show()

実行結果は下記のようになります。

f:id:lib-arts:20190610162039p:plain

次に、ガンマ関数ですが、ベイズ統計のコンポーネントとしてよく出てくるベータ分布がガンマ関数に基づいて作られているのでベータ分布について取り扱う前にガンマ関数を取り扱います。数式で表現すると下記のようになります。

$\Gamma(x)=\int_0^{\infty} t^{x-1}e^{-t} dt$
なかなか複雑なので一旦は下記のコードでグラフを描いて直感的に掴むのが良いかと思います。

import math
import numpy as np
import matplotlib.pyplot as plt

def gamma_vec(input_vector):
res = np.zeros(input_vector.shape[0])
for i in range(input_vector.shape[0]):
res[i] = math.gamma(input_vector[i])
return res

x = np.arange(0.05,5,0.05)
y = gamma_vec(x)

plt.plot(x,y)
plt.show()

下記が実行結果になります。

f:id:lib-arts:20190610165015p:plain
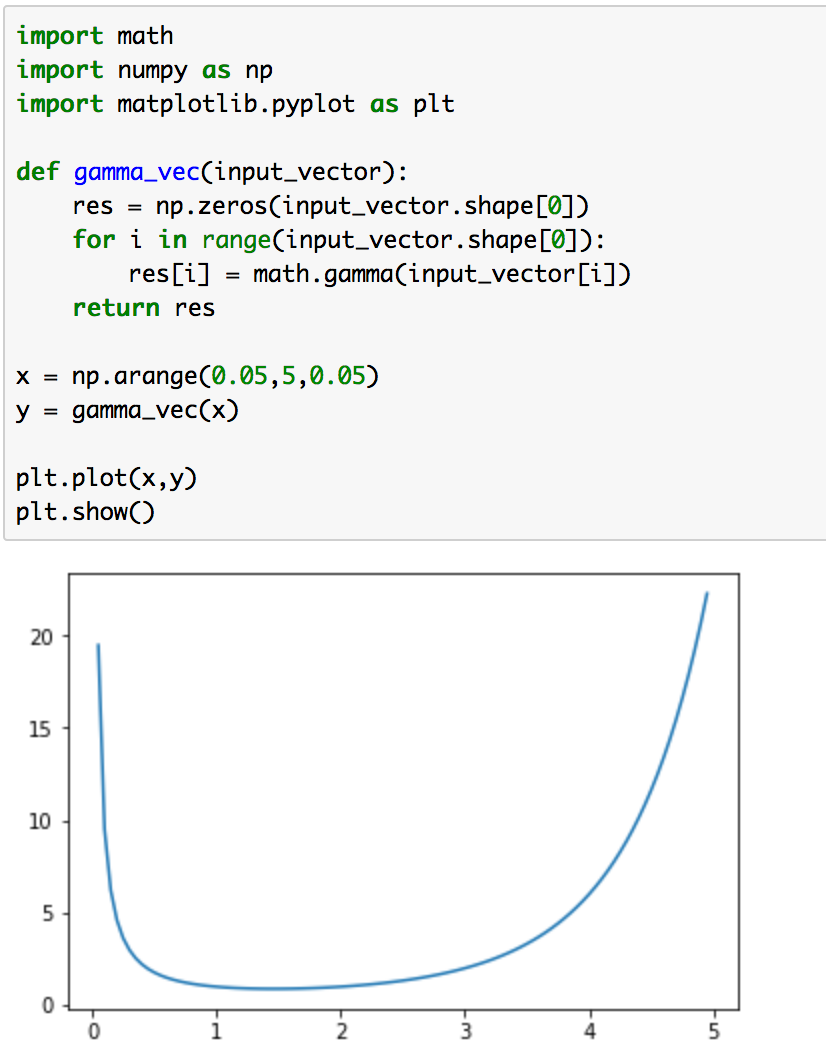
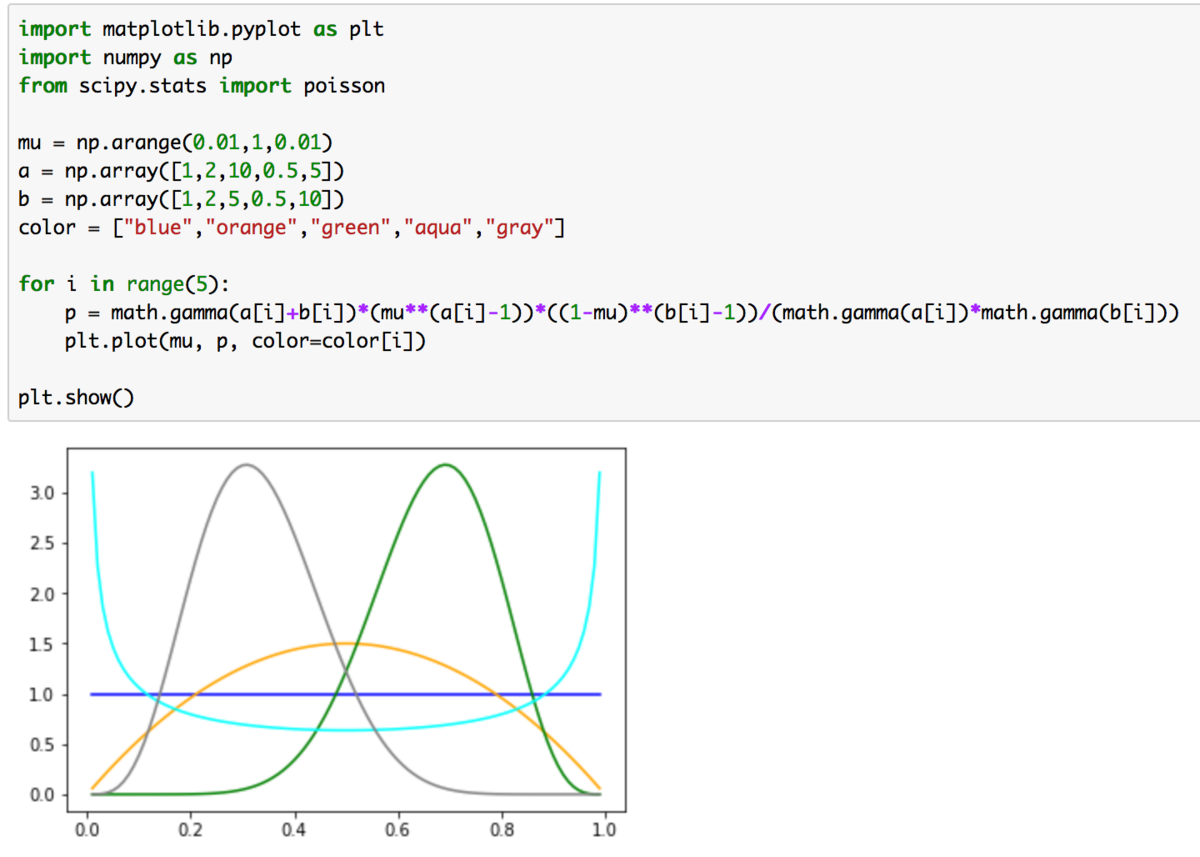
下に凸の関数になっていることが確認できます。このガンマ関数を用いて計算されるのがベータ分布(beta distribution)になります。ベータ分布の数式は以下になります。
$P(\mu|a,b)=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1}$
ベータ分布の可視化は以下の実装で行うことができます。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import poisson

mu = np.arange(0.01,1,0.01)
a = np.array([1,2,10,0.5,5])
b = np.array([1,2,5,0.5,10])
color = ["blue","orange","green","aqua","gray"]

for i in range(5):
p = math.gamma(a[i]+b[i])*(mu**(a[i]-1))*(1-mu)**(b[i]-1)/(math.gamma(a[i])*math.gamma(b[i]))
plt.plot(mu, p, color=color[i])

plt.show()

実行結果は下記のようになります。

f:id:lib-arts:20190610165044p:plain

4. まとめ
#1ではベイズ統計を考えるにあたってベース知識として知っておきたい確率分布に関して可視化を行いました。特にガンマ関数、ベータ分布については解析的に捉えにくい関数のため、Python実装によって可視化を行うことでイメージがつきやすいかと思われます。
#1では1次元の確率分布を主に取り扱ったので、#2では多変量の確率分布について取り扱っていければと思います。