線形回帰処理のパフォーマンス比較①（解析解）｜Pythonにおける処理高速化をラフに考える #5

このシリーズではPythonの処理高速化についてラフに取り扱っています。
#4ではリストの生成と内包表記について取り扱いました。

#5では単回帰分析の解析解を求める処理について、scikit-learnなどを中心にパフォーマンス比較を行いたいと思います。
以下、目次になります。
1. 問題設定＆サンプル数を変えてscikit-learnを実行する
2. NumPyを用いた実装との処理時間の比較
3. まとめ

1. 問題設定＆サンプル数を変えてscikit-learnを実行する
1節では問題設定と処理のパフォーマンス比較を行います。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
%matplotlib inline

np.random.seed(0)

x = np.arange(-1, 9, 0.1)
x_ = x.reshape(x.shape[0],1)
y = x*2 + 1 + np.random.normal(0, 0.1, x.shape[0])

plt.scatter(x,y)
plt.show()

問題設定としては上記のように回帰分析の問題を設定するとします。ここで、上記ではxの区間が10かつ、各サンプルの幅が0.1なので100個のサンプルを生成しています(サンプル数はx.shape[0]で確認が可能)。
まずはこちらについてscikit-learnを用いて回帰分析を計算してみます。

%%time

print(x_.shape[0])
reg = LinearRegression().fit(x_, y)

print(reg.coef_)
print(reg.intercept_)

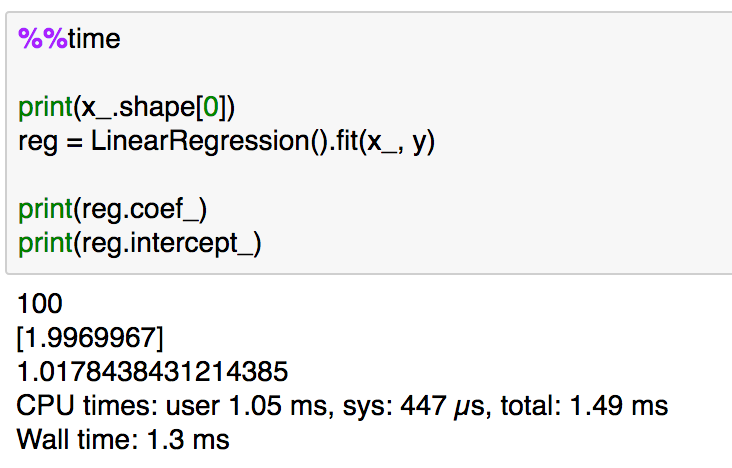
処理時間は大体1msとなっていることが確認できます。以下、サンプルを増やすとどうなるかについて実験してみます。

10倍ずつ増やして、1,000、10,000、100,000で実験した結果が上記です。少しずつ処理時間自体は増えていますが、ここまでは100サンプルと比較した際に5倍以内に収まると考えておいて良さそうです。もう少しサンプル数を増やして実験してみます。

同様に10倍ずつ増やして、1,000,000、10,000,000、100,000,000サンプルについてそれぞれ実行を行ってみました。1,000,000サンプルあたりから、サンプルの増加に比例して処理時間が伸びているとある程度考えて良さそうです(さらに10倍の10億サンプルはサンプルの生成がデフォルトだと難しかったので、1億サンプルを最大とし打ち切るものとしました)。

scikit-learnの処理の確認と、サンプルを増やしての実験について概ね確認できたので1節はここまでとします。

 
2. NumPyを用いた実装との処理時間の比較
2節では1節でscikit-learnを用いて行った実装を他の実装手法を用いて行ってみたいと思います。

上記の記事における実装を用いたパフォーマンス測定を行ってみたいと思います。

100サンプルの実行結果としては上記のように、scikit-learnよりも1.5〜2倍程度速い結果となりました。基本的には処理時間の増加の度合いはscikit-learnを用いた際とそれほど変わらなかったため、以下1億サンプルの場合のみをご紹介します。

1億サンプルを用いた処理としては、上記のようになりました。1節のscikit-learnを用いた実装と比較すると5倍程度高速化が実現されています。サンプル数はそれほど関係なくNumPyを用いて数式ベースで実装した方が数倍程度速いので、高速化が実現できた理由としてはscikit-learnだとロバストに書かれた処理(エラーチェックなど)を省略しているので、少しばかり高速化できたと考えて良いのではと思います。

3. まとめ
#5では回帰分析に関連して、scikit-learnのlinear_modelと数式をNumPyで実装するパターンで解析解の計算にあたってのパフォーマンス比較を行ってみました。数式をNumPyベースで実装する方が数倍程度速くなったので、理論を理解するメリットについてもわずかながら提示できたのではないかと思います。
引き続き#6では勾配法(Gradient Descent)を用いた回帰モデルについて取り扱っていきます。