Pythonで実装する記述統計②（散布図、共分散、回帰分析）｜スクラッチ実装で理解する基礎統計 #2

f:id:lib-arts:20190418215135p:plain

上記のシリーズで機械学習アルゴリズムの実装を行っているのですが、他の内容もできればということで同様のイメージで基礎統計を実装していければと思います。
#1ではデータの整理と要約の方法を取り扱う記述統計学の中から、1変数（1次元）データを取り扱った非常にシンプルな概念であるヒストグラム、平均、分散などを取り扱いました。

#2では記述統計学の中から、2変数（2次元）データを取り扱う考え方である、散布図、共分散、相関係数、回帰分析をご紹介します。
以下目次になります。

1. 前回の復習
2. 散布図の概要とPythonでの実装
3. 共分散や相関係数とPythonでの実装
4. 回帰分析とPythonでの実装
5. まとめ

1. 前回の復習
前回は記述統計学の中から、1変数（1次元）データの取り扱いを行いました。
サンプルデータとしてiris（アヤメ）のデータを用いて、データの外観を俯瞰するヒストグラム、代表的な値を抽出する平均や中央値、データの散らばりを抽出する分散などの概念について定義と実装について追いました。

2. 散布図の概要とPythonでの実装
1節で#1の復習を行いましたので、2節からは今回のメインの内容に入っていければと思います。
まず2節では、1次元のデータの取り扱いにおけるヒストグラムに似た目的で用いられる散布図という概念についてご説明します。散布図は二つの変数に着目して観測された値を2次元平面上に点でプロットを行った図と考えると良いです。
説明だけだとわかりにくいので、前回のirisデータで可視化を行ってみます。下記のコードを実行することによって、散布図を描くことが可能になります。

import matplotlib.pyplot as plt
import pandas as pd
from sklearn import datasets

iris = datasets.load_iris()
X = pd.DataFrame(iris.data, columns=iris.feature_names)

plt.scatter(X["sepal length (cm)"],X["sepal width (cm)"])
plt.show()

上記を実行すると下記のような図を描くことができます。

f:id:lib-arts:20190418203937p:plain
これにより、二つの変数の関係性を可視化することができます。より関係性のある例もある方がこの後の説明上望ましいので、恣意的に二変数が関係するような散布図も用意しておきます。以下のコードも実行してみてください。

import numpy as np

np.random.seed(87655678)
x = (np.random.rand(100)-0.5)*2
y = x + (np.random.rand(100)-0.5)*0.4

plt.scatter(x,y)
plt.show()

コードを実行すると以下のような図を描くことができます。

f:id:lib-arts:20190418203957p:plain
こちらの方が二つの変数が関係あるような図になっているというのは図を見ることで確認できます。

3. 共分散や相関係数とPythonでの実装
2節では散布図を描くことで二変数の関連性を定性的に確認することができました。3節では変数の関係性を定性的な形ではなく、定量的に分析できればと思います。二変数の関係性の指標としては、共分散や相関係数という指標があります。それぞれ以下の数式で表すことができます。
$Cov(x,y)=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\overline{x})(y_{i}-\overline{y})$
$Cor(x,y)=\frac{1}{N}\sum_{i=1}^{N}\frac{(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{Cov(x,x)Cov(y,y)}}$
ここでCovはCovarianceの略で共分散を、CorはCorrelationの略で相関を表しています。数式だけ見てもわけがわからないと思いますので、実装を見ていきましょう。

def calc_cov(x1,x2):
shift_x1 = x1-np.mean(x1)
shift_x2 = x2-np.mean(x2)
res = np.sum(shift_x1*shift_x2)/x1.shape[0]
return res

def calc_cor(x1,x2):
res = calc_cov(x1,x2)/np.sqrt(calc_cov(x1,x1)*calc_cov(x2,x2))
return res

print(calc_cov(X["sepal length (cm)"],X["sepal width (cm)"]))
print(calc_cor(X["sepal length (cm)"],X["sepal width (cm)"]))
print("=====")
print(calc_cov(x,y))
print(calc_cor(x,y))

上記では2節で取り扱った二つのデータについてそれぞれ共分散と相関係数の計算を行っています。結果は以下のようになります。（ソースが若干異なるのははてなの注釈で判断されたため書き直しています。）

f:id:lib-arts:20190421143147p:plain
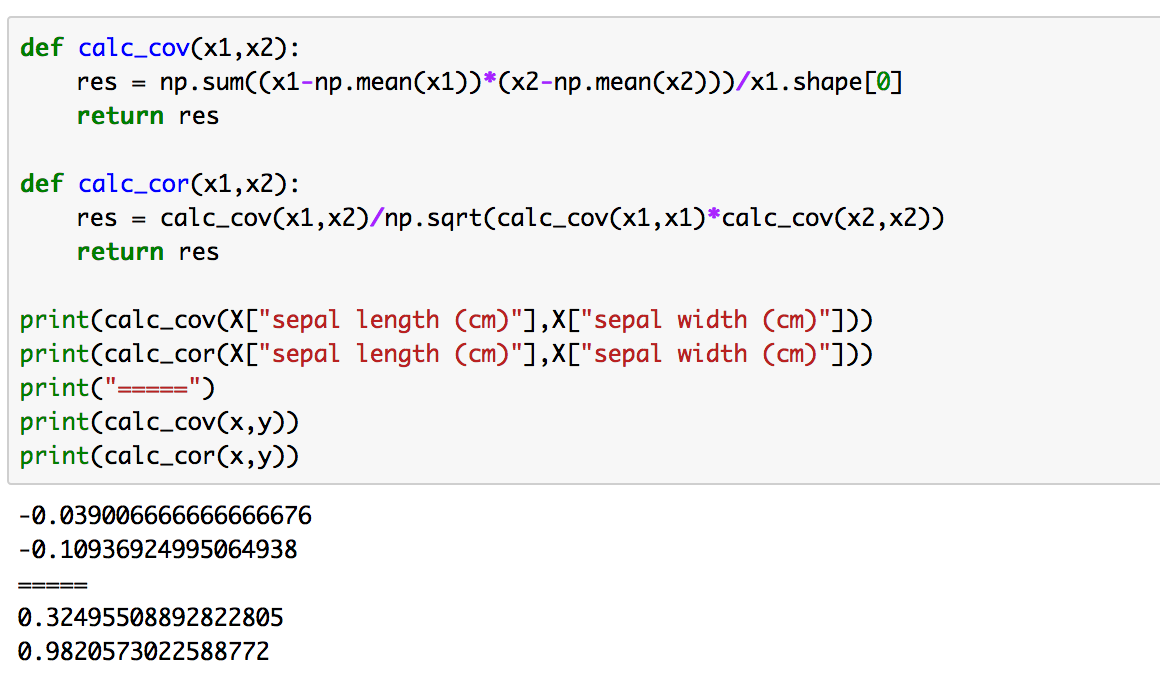
ここで相関係数は-1〜1の値を取る指標で、0.7〜1の値を取っている場合において相関が高いと見ることができます。そのため、二つ目の例は相関係数が0.98なので、相関が強いと考えることができます。

4. 回帰分析とPythonでの実装
4節では回帰分析を取り扱います。回帰分析は、3節で扱った相関係数の値が高い時などに片方の変数（説明変数）でもう片方の変数（目的変数）を予測する問題と考えると良いです。最も簡単な回帰分析は、1次関数である $y=ax+b$ で近似を行う方法です。3節の二つ目の例において相関係数が0.98と高かったので、回帰分析を行ってみましょう。
1次関数で回帰を行うにあたってはパラメータを求める公式が求まっています。（導出にあたっては最小二乗法を用います。）aとbはそれぞれ下記のように計算することができます。

$a=\frac{N\sum_{k=1}^Nx_{k}y_{k} - \sum_{k=1}^Nx_{k}\sum_{k=1}^Ny_{k}}{N\sum_{k=1}^Nx_{k}^2 - (\sum_{k=1}^{N}x_{k})^2}$
$b=\frac{1}{N}(\sum_{k=1}^{N}y_{k}-a\sum_{k=1}^{N}x_{k})$
上記を実装したのが下記になります。

a = (100*np.sum(x*y) - np.sum(x)*np.sum(y))/(100*np.sum(x**2) - np.sum(x)**2)
b = (np.sum(y)-a*np.sum(x))/100
print(a,b)

plt.scatter(x,y)
plt.plot(x,a*x+b,color="green")
plt.show()

上記を実行すると以下のようになります。

f:id:lib-arts:20190502145234p:plain
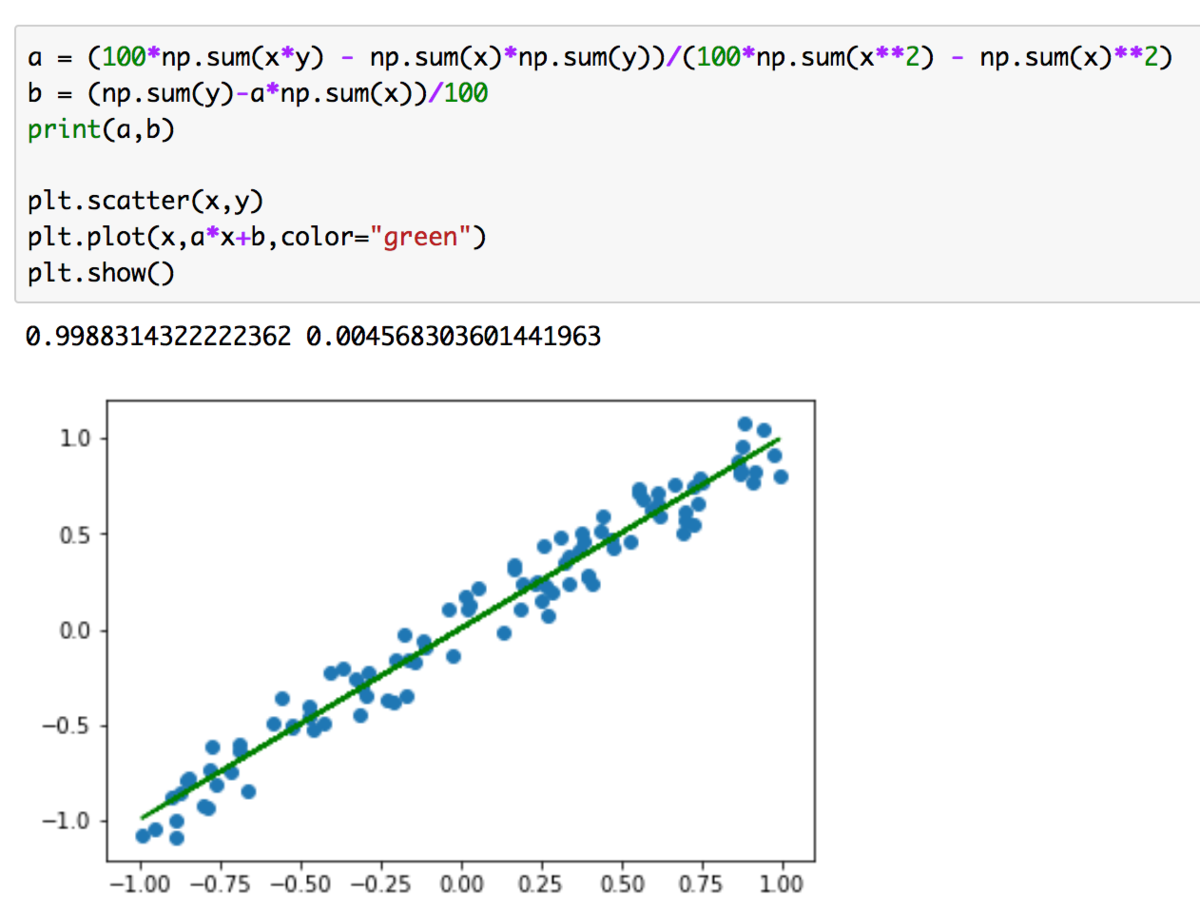
サンプルの中心を通っていることが確認できるので、予測のための規則ができていることがわかります。