2020-11-15

教養(Liberal Arts)の意義とエリートの役割について｜Liberal Artsを考える #1

LiberalArts

f:id:lib-arts:20201115200216j:plain

現代社会では「スキルアップの必要性」があちこちで主張されるのをよく目にします。が、そのうちの多くは「インスタント食品やサプリメントを食べて、健康になりましょう」のような内容を表面上だけ変えての内容であることもあり、それらについての反論なども目にします。
関連の質問をいただくこともあるので時折回答しているのですが、この際に重視しているのは当ブログのタイトルでもある、「Liberal Arts」です。結局のところ、「〇〇を知ったら良い」というスキルはすぐにコモディティ化するなど、本質的にあまり意味のあるものではありません。一方で、「Liberal Arts」的な視点を持っていると、学習が有機的に結びついてくるので、知らないことを学習する際にも大きなアドバンテージを持つことが可能になります。
また、近年エリート(いわゆるインテリや上級国民)から「Liberal Arts」的な視点が抜けているようにも見えるので、「Liberal Arts」について論じた後に改めてエリートの役割についても考えてみたいと思います。
以下、目次になります。
1. 「Liberal Arts(教養)」とは何か
2. 「Liberal Arts」を学ぶ意義
3. エリートに求められる「Liberal Arts」的な視点
4. 「豊かさの追求」としての「Liberal Arts」
5. まとめ

1. 「Liberal Arts(教養)」とは何か
1節では「Liberal Arts(教養)」とは何かについて簡単に確認したいと思います。Wikipediaの記載だと、「個人の人格や学習に結びついた知識や行いのこと。これに関連した学問や芸術、および精神修養などの教育、文化的諸活動を含める場合もある」が概要とされています(https://ja.wikipedia.org/wiki/教養)。また、リベラルアーツ(LiberalArts)も同様の文脈で論じられることが多いので確認します。リベラルアーツは「ギリシャ・ローマ時代に理念的な源流を持ち、ヨーロッパの大学制度において中世以降、19世紀後半や20世紀まで、人が持つ必要がある技芸（実践的な知識・学問）の基本と見なされた自由七科のこと」のように記載されています(https://ja.wikipedia.org/wiki/リベラル・アーツ)。

詳しくはそれぞれのリンク先を参照いただければと思いますが、ざっくりいうと「一般常識や世の中の事象を学術的な(論理的にある程度の正統性がある)視点を取り入れつつ洗練したもの」くらいの認識で良いのではと思います。

・数学(理系の高校〜大学2年生レベル)、統計
・語学(英語＋第二外国語の簡単なレベル)
・政治経済(憲法、政治学、ミクロ経済、マクロ経済、会計)
・理科(物理、化学、生物、地学の中学〜高校レベル)
・工学(各分野の概論、グラフ理論、ゲーム理論、プログラミング基礎)
・歴史(中学〜高校レベル)
・論理学(必要条件・十分条件、集合、三段論法、詭弁など)

現代社会に照らし合わせて具体的に挙げるとするなら上記でしょうか。当記事では概ね上記を基盤としたその他汎用性の高い学術的知見をイメージするものとします。得意不得意もあると思いますが、どれもある程度のレベルでは抑えておくのが良いのではと思います。

2. 「Liberal Arts」を学ぶ意義
1節では「Liberal Arts」とは何かについて確認しましたが、2節ではそれを受けて「Liberal Arts」を学ぶ意義について考えたいと思います。「スキルアップ」としてよりも「Liberal Arts」として学ぶ方が有意義な点はどの辺にあたるのでしょうか。

① 汎用性の度合いが違う
-> スキルアップとして学ぶ際は「知識」として身につけることが多いですが、「Liberal Arts」として学ぶ際は「理解」として身につけることが多いです。「知識」と「理解」を比較した際に、「理解」の方が広い範囲に適用できるため、汎用性が圧倒的に高いです。「数学の演習」などがわかりやすい例ですが、「教科書の内容を知っている」のと「教科書の内容を理解している」だと大幅にテストの点数が違ったかと思います。

② シンプルに考えることができるようになる
-> 「知識」よりも「理解」として身につけると、一度に考えなければならない内容を減らすことができます。数学の「微分」一つ取っても、定義式から派生して「理解」しておけばほとんどの内容は関連で把握することが可能になります。

③ 大局的な視野を持てる
-> 社会で生じる問題は様々な要素が関連した非常に複雑な問題であることが多く、一つの視点からだけ考えても意味がないということが多くあります。こんな時に単なる「知識」では異なる分野から派生する「知識」間の整合性を調整することができません。このような時に「Liberal Arts」的な視点で様々な分野について「理解」しておくことで、異なる分野の知見を優先順位をつけながら結びつけることが可能になります。

筆者の考えを上記にざっくりとまとめました。思いついた内容でまとめたので、MECEにはなっていないと思いますが、イメージとしては十分だと思います。有機的に様々な分野の知見を組み合わせて複雑な問題に取り組みやすく、新しい知識の獲得が速いくらいのイメージでご理解いただけたら良いのではと思います。

3. エリートに求められる「Liberal Arts」的な視点
3節ではエリートに求められる視点としての「Liberal Arts」について考えてみたいと思います。題材として面白いのは「コロナショック」のような不測かつ複雑な事態への対応です。たとえば50年前の日本の政治家や官僚であればもう少しうまく対処できていたのではないかと筆者は考えているのですが、いかがでしょうか。アジア圏では何らかの理由である程度被害が少なくなっており、その中でも日本の被害は比較的大きくかつ経済的なダメージも大きいという結果になったというのがある程度一般的な評価ではないでしょうか。
対案を出さないとフェアではないので、理由について考えてみます。

① 検査と隔離を徹底しないことでリスクを放置した(現状把握を重視しなかった)
② メリハリのない自粛要請(個々人の自粛に頼り過ぎるとオオカミ少年のような状況が生じる)
③ 自助中心(平時対応とは切り分けるべき)

これにより、ある程度社会全体がダメージを受けたのではないかと思います。

以前の記事でも論じましたが、「財政破綻」については「名目上の国債残高」よりも「主権国家の構成員のコンセンサス」が重要だと思います。無論、「自己責任」という目線も大事ですが、たとえば国民の10％が生活の基盤をなくすと考えると経済へのダメージはいかほどでしょうか。また、外国人労働者(技能実習生)の一部が失職に際し犯罪を犯しているという話も、ある程度全体の流れを元に考えたらそうなるだろうと予測できるはずです。

ということで、現在のエリート(官僚のようなインテリや政治家のような上級国民を指すものとします)は少し調べて考えればわかることを全く考慮していないように見えます。何のためのエリートなのでしょうか。清廉潔白であり過ぎる必要はないですが、「エリートとは地位ではなく役割である」ということはせめて理解して欲しいものです。

もう少し突っ込むなら大局的な視野を持てていないということもあるのではと思います。関連として昨今の教育において、「専門性」がやたら注目されているというのも少し危惧しなければならないのかもしれません。何か一つで結果が出せればそれで良いのでしょうか、コスパとしては良いのかもしれませんがロボットみたいに「部分最適化」しかできない人間の育成を重視して、適切な社会の運用ができるのでしょうか。

4. 「豊かさの追求」としての「Liberal Arts」
3節は少々批判的な内容になりましたので、4節では改めて「豊かさの追求」として「Liberal Arts」について論じてみようと思います。「スキルアップが必要」のような文脈での学習はあまり望ましいものではないと思いますが、「〇〇さえやればいいんでしょ」的な考えが裏にあるからなのではないかと思います。
一方で「Liberal Arts」はどうでしょうか。確かに、すぐに役に立つ内容ではないかもしれませんが、学生時に身につけた内容であっても本質を抑えた内容は今だに役に立つということは多くはないでしょうか。ちょっとした算数が日常生活でも役に立つのとは同様に、一度学んだ内容が様々な状況で関係してくるなど、「Liberal Arts」は非常に奥の深いものです。

また、「豊かさの追求」についてはいかがでしょうか。「民主主義(Democracy)」という発想が現代社会における「豊かさ」を実現するための考え方ではないか、というのが筆者の考えです。

というのも、上記でもまとめましたが「結果平等」的な社会よりも、「機会平等」的な社会の方が健全ではないか、と考えるためです。身分や資産、能力に関わらず、「一人一票」を行使できるこの仕組みは、「機会平等」を実現するための重要な制度ではないかと思います。

とはいえ、「民主主義(Democracy)」の運用にあたって、一人一人が意思決定をするというのは大変難しい話です。広告などによるプロパガンダにもある程度左右されるかもしれません。ですが、やはり一人一人が考えて意思決定を行なっていく仕組みというのは重要で、そのための判断基準として「Liberal Arts」は大きな指針になるのではないかと思います。

上記では「選択の自由がない」ことをある程度「奴隷」的にみなしました。「選択の自由」こそが「豊かさ」であり、「自由を行使するための学問」こそが「Liberal Arts」だと思います。

5. まとめ
当記事では「Liberal Arts」の意義やエリートに求められる視点、そして「豊かさの実現手段」としての「Liberal Arts」について考えてきました。「民主主義(Democracy)」的な集団の意思決定にとどまらず、個々人の意思決定など、様々な状況において「Liberal Arts」的な考え方とは参考になるのではないかと思います。
#1では概論的にまとめましたが、#2以降ではもう少し具体的な内容について論じていけたらと思います。

2020-11-13

パフォーマンス測定とNumPyを用いた簡単な高速化｜Pythonにおける処理高速化をラフに考える #1

Python NumPy SpeedUp

f:id:lib-arts:20201113203327j:plain

基本的にプログラミングは動けば良い派で可読性の高さを優先することが多いですが、処理の高速化が必要な際もあるので、Pythonを用いた処理高速化について考える新規シリーズを作成いたしました。
最初から難しく考えると大変なので、しばらくは緩めに進め、徐々に内容を本格化していければと思います。（しばらくは体系立った解説にはしませんので、そういう意味ではあまり参考にしないようにお願いします）
#1では繰り返し文の処理をmapを用いて置き換えた際の簡単なパフォーマンス比較を行います。
以下、目次になります。
1. パフォーマンス測定に関して
2. mapを用いた繰り返し文の置き換えについて
3. まとめ

1. パフォーマンス測定に関して
1節ではパフォーマンス測定に関して取り扱います。Jupyterでは「%%time」を用いるとある程度簡単に処理にかかった時間の計測ができるので、当シリーズでは一旦「%%time」を用いるものとし、以下簡単にご紹介します。

%%time

a = 1
print(a)

まずは上記を実行してみます。実行結果は下記のようになります。

f:id:lib-arts:20201113203529p:plain
上記ではtotalが87µsとなっており、ほぼ一瞬で終了していることがわかります。あまり軽い処理だとパフォーマンス測定には適していないので、以下、繰り返し文を用いて少し処理の負荷を大きくしてみます。

%%time

a = 0
for i in range(10000):
idx = i+1
a += idx

print(a)

f:id:lib-arts:20201113203622p:plain

上記ではtotalが1.86msとなっており、最初のプログラムより若干時間がかかっていることがわかります。以下、ループの数を増やしてもう少し実験してみます。

f:id:lib-arts:20201113203932p:plain

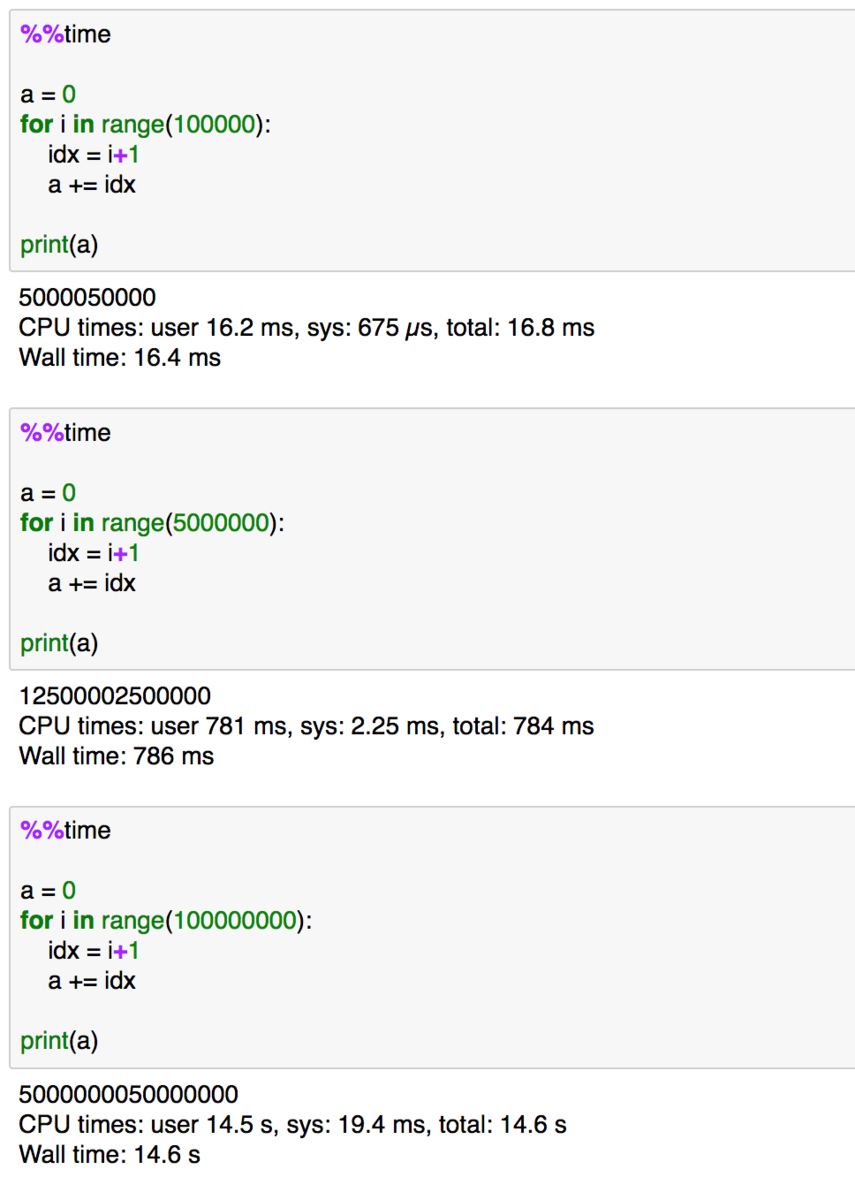
上記は、ループ回数をそれぞれ10万、500万、1億にして実験してみた結果です。徐々に時間がかかるようになり、ループが1億だと10秒以上かかる結果となりました。このように「%%time」を用いることで、Jupyter上で簡単に計測を行うことができるので、しばらくはこちらを用いてパフォーマンス測定を行なっていくものとします。

パフォーマンス測定について簡単な確認はできましたので1節はここまでとします。

2. NumPyを用いた簡単な高速化
2節では1節のプログラムの高速化について考えます。Pythonにおいては繰り返し文(for文など)は遅いと言われることが多いので、NumPyを用いて1節で取り扱ったプログラムの高速化を試みてみます。

%%time

x = np.arange(100000000)+1
print(np.sum(x))

上記を実行すると下記のようになります。

f:id:lib-arts:20201113204935p:plain

計算結果自体は1節の1〜1億までの和を計算した結果と同じですが、処理時間についてはtotalで849msと、1節の15分の1程度に抑えられていることがわかります。このようにちょっとした処理を書き換えるだけでも、高速化が可能になります。もう少し実験を行なってみます。

f:id:lib-arts:20201113210717p:plain
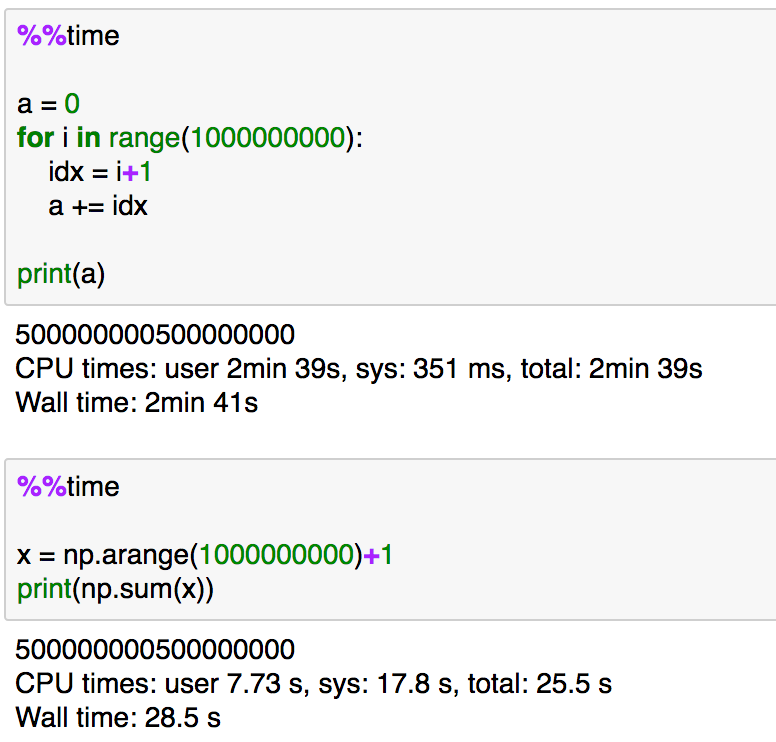
上記はさらにもう1桁上げ、1〜10億までの結果を計算して比較した結果です。繰り返し文を用いた実装の方が時間はかかっていますが、NumPyの方もそれなりにかかっていることがわかります。

f:id:lib-arts:20201113210042p:plain

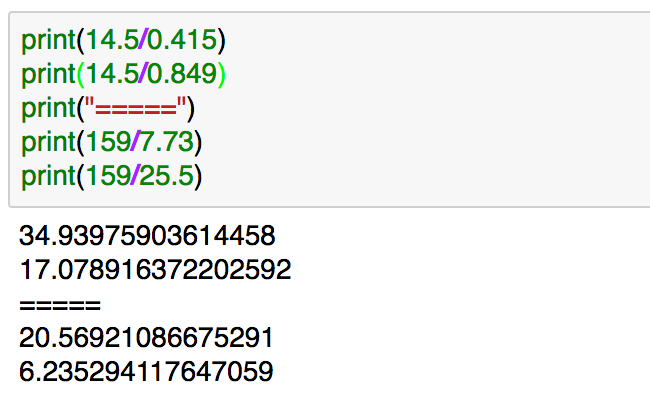
確認するとNumPyの実装の方がsysにかかる時間が多いので、totalの比とuserの比に分けて計算してみた結果が上記です。NumPyはuserよりもsysに時間がかかりやすいことがある程度見て取れます。

このように単純な和を計算するプログラムでも様々な要素が絡んでくるので、色々と試しつつ内部処理なども含めて高速化を行なっていくのが良さそうです。今回はラフに確認を行えれば十分だったのでここまでとします。

3. まとめ
#1では「%%time」を用いたパフォーマンス測定と、NumPyを用いた簡単な処理の高速化について取り扱いました。
#2ではmapを用いた繰り返し文(for文)の書き換えについて確認します。

2020-11-05

周辺正規分布(Marginal Gaussian distributions)｜改めて理解する多次元正規分布 #3

PRML Machine Learning statistics

f:id:lib-arts:20201105153023p:plain

当シリーズは多次元正規分布を改めて理解しようということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

上記テキストのSection2-3の"The Gaussian Distribution"を中心に関連文脈の確認を行なっていきます。

参照テキストは2次元に限らない形式で記述されている項目もありますが、多次元に関連する一般的な式で議論するとややこしいので、当シリーズでは基本的に2次元ベースで考えていきたいと思います。
#1ではマハラノビス距離の図的な意味合いについて、#2では条件付き正規分布について確認しました。

#3では周辺正規分布(Marginal Gaussian distributions)について確認します。

以下、#3の目次になります。
1. 理論の流れの把握
2. Python実装による確認
3. まとめ

1. 理論の流れの把握
1節では参照テキストのSection2-3-2の"Marginal Gaussian distributions"の把握を行います。計算が複雑ですが、論理の流れ自体は基本的には平方完成がベースでシンプルなので、大元の記載が難しい場合は2次元に置き換えて大枠を掴むことを優先するのが良いかと思います。

f:id:lib-arts:20201105153518p:plain

さて、まず周辺分布(Marginal distributions)の定義ですが上記の(2.83)式のようになります。少しややこしいですが、 $x_b$ について積分し、 $x_a$ についての確率分布を得ていることを念頭に把握しておくと良いかと思います。また、議論の流れとして、条件付き分布と同様に指数関数の中の二次形式(quadratic form)を考えることで、周辺分布の $p(x_a)$ の平均(mean)や共分散(covariance)を考えるとしています。

f:id:lib-arts:20201105161649p:plain

$x_b$ に関する積分を考えるにあたって、上記の(2.84)式ではマハラノビス距離を $x_b$ に関する項だけ抜き出し、 $x_b$ に関して平方完成(completing the square)を行っています。ここで式を整理するために、(2.85)式のように $m$ という文字を定義しています。

f:id:lib-arts:20201105162044p:plain

f:id:lib-arts:20201105163030p:plain

さて、(2.84)式をベースにした積分を考えるにあたって、 $x_b$ に関する項は(2.84)式の右辺の第1項のみなので、この積分を上記の(2.86)式で考えています。これは正規分布のせい聞かされていない状態とも見ることができるので、積分後の値はこの後に $x_a$ について考えていくにあたっては考慮しなくて良いとされているようです(本文のニュアンスが掴み切れてないのですが、その後の式展開を見ると(2.86)式は考慮されていないのでこの記述で正しいと思います)。したがって(2.84)式の右辺の第2項と、(2.70)の式からこれまで考慮しなかった式を引っ張ってきて(2.87)式を導出しています。(2.87)式を $x_a$ の関数と見た際に、(2.88)式と(2.89)式がそれぞれ共分散(2次元で考えた場合は分散)と平均を表しています。

f:id:lib-arts:20201105163413p:plain

残りの議論は省略しますが、周辺分布の平均と共分散は上記の(2.92)式と(2.93)式になり、これは元々の $x_a$ の平均と共分散( $x_a$ がスカラーの場合は分散)に一致しているということがここで確認できます。

2. Python実装による確認
実装については#2と図の内容が同様なので、改めて比較として載せます。

from scipy.stats import norm

x = np.arange(-1, 2, 0.01)
y_1 = norm.pdf(x, loc=0.64, scale=0.51)
y_2 = norm.pdf(x, loc=0.5, scale=1)

plt.plot(x, y_1, color='red')
plt.plot(x, y_2, color='blue')
plt.show()

上記を実行すると下記のようになります。

f:id:lib-arts:20201104171626p:plain

上記の青が周辺分布、赤が $x_b=0.7$ における条件付き分布となっています。

3. まとめ
#3では周辺正規分布(Marginal Gaussian distributions)について取り扱いました。
#4では参照テキストSection2-3-3のベイズの定理の導入について確認します。

2020-11-04

条件付き正規分布(Conditional Gaussian distributions)｜改めて理解する多次元正規分布 #2

PRML statistics Machine Learning

f:id:lib-arts:20201103221132p:plain

当シリーズは多次元正規分布を改めて理解しようということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

上記テキストのSection2-3の"The Gaussian Distribution"を中心に関連文脈の確認を行なっていきます。

参照テキストは2次元に限らない形式で記述されている項目もありますが、多次元に関連する一般的な式で議論するとややこしいので、当シリーズでは基本的に2次元ベースで考えていきたいと思います。
#1では参照テキストのSection2-3の冒頭部を参考に、マハラノビス距離の図的な意味合いを掴みました。

#2では条件付き正規分布(Conditional Gaussian distributions)について確認します。

以下、#2の目次になります。
1. 理論の流れの把握
2. Python実装による確認
3. まとめ

1. 理論の流れの把握
1節では理論の流れについての把握を行います。

f:id:lib-arts:20201103222208p:plain

まずは問題設定の確認から行います。上記では多次元正規分布を仮定した設定になっていますが、2次元とみなして話を見ていくで十分だと思いますので、当記事では基本的に2次元前提で考えていきます。共分散行列(covariance matrix)について取り扱った(2.67)については、共分散行列が対称行列であることから $\Sigma_{ba}=\Sigma_{ab}^{T}$ が成立するとされています(転置が入るのはD-M次元とM次元を考慮しているためです)。

f:id:lib-arts:20201103222939p:plain

次に、式中で共分散行列の逆行列を取り扱う手間を減らすために、上記の(2.68)式のように精度行列(precision matrix)を導入しています。また、(2.69)式では共分散行列の(2.67)式と同様な意味で行列を分割(partition)して考えています。

f:id:lib-arts:20201103223604p:plain

ここまでの定義を元にした際に、マハラノビス距離は上記の(2.70)式のように表すことができます。(2.70)式を $\mathbf{x}_{a}$ の関数と見た際に、二次形式の形になっているので、条件付き分布の $p(\mathbf{x}_{a}|\mathbf{x}_{b})$ は正規分布(Gaussian)であろうことがわかります。そこで、議論における目標を $p(\mathbf{x}_{a}|\mathbf{x}_{b})$ の平均と共分散行列を求めることにおく、とここでは記載されています。

f:id:lib-arts:20201103225055p:plain

$\mathbf{x}_{a}$ の二次形式として(2.70)を考えるにあたって、上記の(2.71)式のようにみなして平方完成(completing the square)を考えることで、分布の中心(mean)の導出を行なっています。

f:id:lib-arts:20201103225627p:plain

f:id:lib-arts:20201103225654p:plain

上記の議論で $\mathbf{\mu}_{a|b}$ を(2.75)式において、Λを用いた形で導出しています。(2.75)式ではxの係数が $\mathbf{\Sigma}_{a|b}^{-1} \mathbf{\mu}_{a|b}$ に一致することを用いて導出を行なっています。難しく書かれていますが、計算のイメージとしては $(x-a)^2$ の形に平方完成して、 $a$ を平均とみなすという議論を行なっているというだけです。また、 $\mathbf{\Sigma}_{a|b}$ については(2.73)式でΛの式で導出されています。

f:id:lib-arts:20201103230951p:plain

(2.73)式と(2.75)式はどちらも精度行列Λを用いて表されているので、これを共分散行列Σの形式にするにあたって、上記は議論を行なっています。結果として、(2.75)式は(2.81)式、(2.73)式は(2.82)式を導出しています。

大まかな議論の流れを抑えることはできましたので、1節はここまでとします。

2. Python実装による確認
2節では1節の内容を具体的な例のPython実装を通して改めて確認を行います。

f:id:lib-arts:20201103221132p:plain

冒頭にもありました上記の再現をPythonを用いて行うというのをここでの目標としたいと思います。下記が問題設定になります。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.stats import multivariate_normal
%matplotlib inline

mu = np.array([0.5, 0.5])
sigma = np.array([[1, 0.7], [0.7, 1]])

x, y = np.mgrid[0:1.01:0.01, 0:1.01:0.01]
pos = np.dstack*1
rv = multivariate_normal(mu, sigma)

plt.contour(x, y, rv.pdf(pos), colors='g', linewidths=1)
plt.plot(x, x*0+0.7, color='red')
plt.show()

f:id:lib-arts:20201104151309p:plain

上記の問題において、条件付き正規分布を確認していきます。上記は、 $\mathbf{\mu} = \left(\begin{array}{c} 0.5 \\ 0.5 \end{array}\right)$ 、 $\mathbf{\Sigma} = \left(\begin{array}{c} 1.0　0.7 \\ 0.7　1.0 \end{array}\right)$ の2次元正規分布の確率密度関数をPythonを用いて図式化したものになります。

ここで(2.81)式と(2.82)式を二次元で解釈すると、
$\displaystyle \mu_{x_a|x_b} = \mu_{a} + \frac{\sigma_{ab}}{\sigma_{bb}} (x_{b} -\mu_{b})$

$\displaystyle \sigma_{x_a|x_b} = \sigma_{aa} - \frac{\sigma_{ab}^2}{\sigma_{bb}}$

のようになります。ここに具体的に数字を入れて計算すると下記のようになります。
$\displaystyle \mu_{x_a|x_b} = 0.5 + \frac{0.7}{1} (x_{b} - 0.5) = 0.15 + 0.7 x_{b}$

$\displaystyle \sigma_{x_a|x_b} = 1 - \frac{0.7^2}{1} = 0.51$
これを元にPython実装を行います。

f:id:lib-arts:20201104171626p:plain

実行結果は上記のようになります。参照テキストと同様に $x_{b}=0.7$ の際のグラフを赤で記しました。また、青についても参照テキストと同様に平均0.5、分散1の正規分布を描きました。

結果が多少異なって見えるのは参照テキストでは多次元分布を取り扱っているのが大きいと思います(途中で導出ミスがある可能性もありますが、それ以上に2次元と多次元の違いが大きいのではという印象です)。

3. まとめ
#2では条件付き正規分布(Conditional Gaussian distributions)について確認しました。
続く#3では周辺正規分布(Marginal Gaussian distributions)について取り扱っていきます。

*1:x, y

2020-11-03

マハラノビス距離(Mahalanobis distance)と多次元正規分布｜改めて理解する多次元正規分布 #1

PRML statistics Machine Learning

f:id:lib-arts:20201103155414p:plain

正規分布は様々なモデリングで前提として使用する、基本かつ非常に便利な分布ですが、1次元だと比較的シンプルに取り扱うことができますが、多次元正規分布となると様々なトピックが出てきて少し難しそうな印象を受けます。
とはいえ、多次元正規分布関連の導出は非常に重要なものが多く、多くの理論展開のベースとなりやすいです。そこで、多次元正規分布を改めて理解できるように、新規でシリーズを作成しました。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer

参考としては、上記のSection2-3の"The Gaussian Distribution"を中心に確認していきます。

参照テキストは2次元に限らない形式で記述されている項目もありますが、多次元に関連する一般的な式で議論するとややこしいので、当シリーズでは基本的に2次元ベースで考えていきたいと思います。
#1では参照テキストのSection2-3の冒頭部を参考に、マハラノビス距離の図的な意味合いを掴みたいと思います。

以下、#1の目次になります。
1. 正規分布の数式とマハラノビス距離
2. 座標変換による分布の回転
3. まとめ

1. 正規分布の数式とマハラノビス距離
1節では正規分布の数式の確認と、数式中に出てくるマハラノビス距離(Mahalanobis distance)について取り扱います。

f:id:lib-arts:20201103164400p:plain

参照テキストにおいて正規分布の数式は上記のように表されており、(2.42)式が1次元、(2.43)式が多次元(参照テキストではD次元となっている)の式を表しています。少し式の形は違うものの、基本的には同じ数式の形になっていることは抑えておくと良いと思います。また、(2.42)式は変数がスカラー $x$ である一方で、(2.43)式はベクトルを変数として取り扱います。が、左辺の値自体はどちらも確率密度関数の値でスカラー関数となっていることは間違えないように気をつけると良いです。

f:id:lib-arts:20201103165851p:plain

f:id:lib-arts:20201103165910p:plain

さて、(2.43)式の解釈にあたって、expの中身を取り出したのが上記の(2.44)式で表されたマハラノビス距離(Mahalanobis distance)です。またこの際に分散共分散行列のΣが単位行列(identity matrix)の場合は、マハラノビス距離はユークリッド距離(Euclidean distance)と一致します。また、(2.44)式のマハラノビス距離の式は、ベクトルxに関する二次形式(quadratic form; xに関して二次の形)であることも、抑えておきたいところです。

この(2.44)式で表したマハラノビス距離は、(2.43)式における指数関数(exp)の中身となっていることを強調した上で、1節はここまでとしたいと思います。

2. 座標変換による分布の回転
2節では1節で確認したマハラノビス距離の数式を考えることで、座標変換によって分布を回転させると考えることができることについて確認していきます。

f:id:lib-arts:20201103155414p:plain

上記は冒頭の図と同じですが、こちらを導出するのが2節の主な流れです。要はxをベースとする数値をyをベースとする数値に変換する(回転させる)ことで、共分散が0でない際の計算を行うようなイメージです。

f:id:lib-arts:20201103171832p:plain

論理展開の流れとしては、1節で取り扱ったxについての(2.44)式を上記の(2.50)式のようなyを元にした式に変換するという流れです。以下、固有値ベクトルなどの考え方を用いた(2.44)式から(2.50)式への導出を確認していきます。

f:id:lib-arts:20201103171941p:plain

まず上記では、(2.45)式で分散共分散行列のΣの固有値、固有ベクトル(eigenvectors)のuを考えています。ここで、固有ベクトルは向きが議論上重要で、スカラーについてはある程度恣意的に決めて良いことから、正規直交系（orthonormal system; 難しければ固有ベクトルの大きさが1であるとざっくり抑えておいてください）を仮定しているのが(2.46)式と(2.47)式です。

f:id:lib-arts:20201103172809p:plain

次に上記では、固有ベクトルのuについて論理展開を行なっています。(2.51)式のようにyを定義することで、(2.44)式のマハラノビス距離を(2.50)式のように変換することができます。これを元に、(2.52)式のように行列Uによってxに関する座標を回転させ、yに変換すると考えることができます。

3. まとめ
#1ではマハラノビス距離の中身に着目して、座標変換による正規分布の回転について見てきました。この辺の議論は主成分分析にもつながってくるので、必見です。
#2では多次元正規分布における条件付き確率分布を取り扱いたいと思います。

2020-11-02

変分推論の概要と簡単な実装例｜Python実装で理解する変分推論(VariationalInference) #5

Machine Learning EM-Algorithm statistics VariationalInference

f:id:lib-arts:20201022172002p:plain

当シリーズはPython実装を通して変分推論を理解していこうということで進めています。下記などを主に参照しています。

Pattern Recognition and Machine Learning | Christopher Bishop | Springer
#3、#4ではEMアルゴリズムについて確認しました。

基本的な論理展開については大体抑えられたかと思いますので、#5からは変分推論の内容に入っていきます。
以下、今回の目次になります。
1. 変分推論の概要
2. 簡単な実装例
3. まとめ

1. 変分推論の概要
1節では変分推論の概要について簡単に取り扱います。

f:id:lib-arts:20201024183044p:plain

#4で上記を確認しましたが、EMアルゴリズムを考えるにあたって導入した確率分布 $q$ ですが、変分推論では同様の数式に対し、 $q$ に対する最適化を考えます。変分推論のベースとなっている変分法では関数を入力とする汎関数に対する最適化を行いますが、変分推論では確率分布 $q$ に関する最適化を行います。

f:id:lib-arts:20201102002124p:plain

f:id:lib-arts:20201102002319p:plain

さて、汎関数の最適化にあたってのアプローチとして、参照テキストでは主に上記の2つのアプローチが紹介されています。ざっくりまとめるなら、「①確率分布のq(Z)に制約を設ける(restricted family of distributions)」、「②パラメトリックな確率分布のq(Z|ω)を設定する」の2つが紹介されています。参照テキストのSection10-1-1では①のアプローチが取られているので、以下そちらについて確認していきます。

f:id:lib-arts:20201102002745p:plain

分布の分解にあたっては、上記の式(10.5)のように、同時分布を独立した確率分布の積で表すことで、各次元の相関を取り除いています。

f:id:lib-arts:20201102003012p:plain

(10.5)式を(10.3)式に代入し、数式変形を行っているのが(10.6)式です。また、(10.7)式と(10.8)式は式の定義なので、抑えておきましょう。一見難しく見えますが、単に(10.6)式の第1項の置き換えを試みているだけですので、単にそういう風に定義して式を整理しただけと理解すれば十分です。ここで、(10.6)式が負のKLダイバージェンス(negative Kullback-Leibler divergence)を表していることに着目すると、 $q_{j}$ の最適解を得ることができます。

f:id:lib-arts:20201102004022p:plain

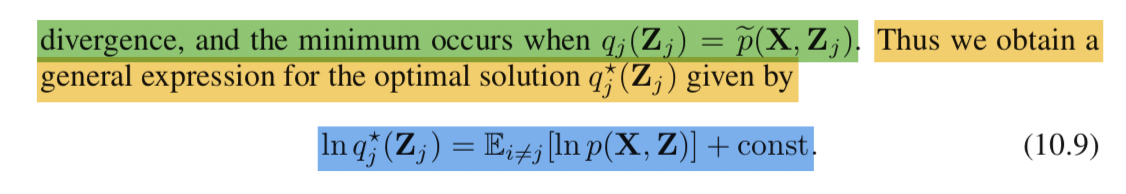
$q_{j}$ の最適解は上記の(10.9)のように求めることができます。

ここまでで分布の分解を利用した変分推論の一般的な導出の流れについて確認できたかと思います。続く2節ではこの例を2次元の正規分布に適用した例の理論展開と簡単な実装を確認していきます。

2. 簡単な実装例
2節では2次元の正規分布における分布の分解を利用した変分推論について確認していきます。

f:id:lib-arts:20201102004525p:plain

まず問題設定ですが、上記のように2次元の正規分布を $q_{1}(z_{1})q_{2}(z_{2})$ のように分解して変分推論を行うとしています。

f:id:lib-arts:20201102004814p:plain

f:id:lib-arts:20201102004832p:plain

(10.9)式に基づき $q_{1}(z_{1})$ と $q_{2}(z_{2})$ についてそれぞれ最適解を求めると上記のようになります。(10.13)式と(10.15)式を交互に用いることで推論を行っていくことができます。ここで $z_{1}$ と $z_{2}$ の期待値はそれぞれ、その時点での $m_{1}$ と $m_{2}$ に該当しています。

少し数式が並んで大変なので、以下具体的にPython実装で確認していきましょう。

f:id:lib-arts:20201102005327p:plain

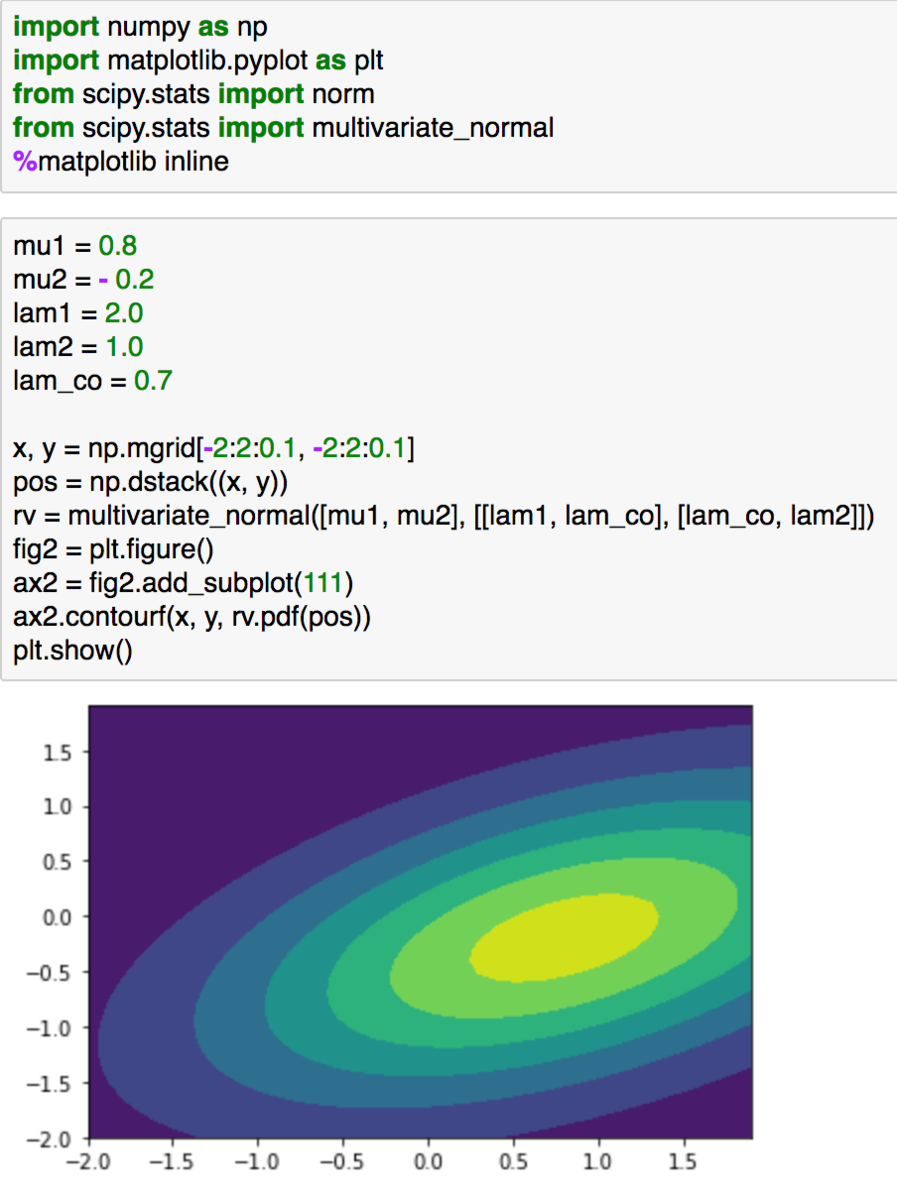
まず、問題設定としては上記のように2次元の正規分布を考えるとします。平均と共分散行列を与えており、共分散に0.7が入っていることで分布が傾いていることが確認できるかと思います。

f:id:lib-arts:20201102005546p:plain

続いて上記は $m_{1}$ と $m_{2}$ に初期値の0を与えた上で、(10.13)式と(10.15)式を交互に実行することであたいの計算を行った結果です。 $m_{1}$ が0.8、 $m_{2}$ が-0.2に収束することで2次元の正規分布と同じ中心を求めることができたと確認ができるかと思います。

このように、分布の分解を用いた変分推論では、各次元に対し交互に値をの更新を行うことで元の確率分布 $p$ をよりシンプルな分布である $q$ で近似を行います。

3. まとめ
#5では変分推論の概要と、分布の分解を用いた確率分布の近似の手法、2次元の正規分布を題材にした実装の確認を行いました。詳しく式の導出についてまでは追いませんでしたが、大体の流れはつかめたかと思います。

2020-10-31

現代社会における奴隷の作り方

Society

f:id:lib-arts:20201031145649p:plain

昨今の「コロナ関連の無利子無担保融資」について、あまり政策としては意味がないのではないかと思っていたのですが、何かに似ているなと思ったら「奨学金」に近いのではと思い至り、少し納得しました。この両者に共通するのは、「見通しがはっきりしない状況でありがたいと思いつつお金を借りる」です。
もちろん、「借金」というのは必ずしもネガティブな側面だけで考えるべきではないかもしれません。たとえば良い大学に進学し、高収入を得られるようになれば、「奨学金」は意味のあるものにはなるでしょう。が、全員が返済できる見込みはあるのでしょうか、返せない場合はどうなるのでしょうか。

今回のタイトルは「現代社会における奴隷の作り方」としましたが、結局はこれは「奴隷」を作り出す話に構造的には近いのではないかと考えたためです。「奴隷」という言葉自体はあまり良くないかもしれませんが、「奴隷的な状況」を生み出す構造については議論しておくと良いと思われたため、タイトルは少し過激になりました。

さて、批判的な論調は昨今あまりよろしくないとされるので、むしろ肯定的に考え、「奴隷をどのように作り出すか」という視点で考えたいと思います。「奴隷的な状況」が陥る人が多ければ多いほど、社会は良くなる、だから、より多くの人間をそのような状況に置くにはどうしたら良いのか、という視点でこの記事では論じていきます。

以下、目次になります。
1. そもそも奴隷とは何か
2. 不確定な状況における「借金」が意思決定範囲を狭める可能性
3. 逆に「借金」をいかにポジティブに見せるか
4. 過剰供給による「需要と供給」の均衡の崩壊
5. 奴隷が多い社会の素晴らしさを考える

1. そもそも奴隷とは何か
まず、1節では「そもそも奴隷とは何か」について言葉の意味を改めて抑えようと思います。「奴隷」は比喩的に使われることも多いため、意外と意味を抑えている方は少ないのではないでしょうか。
Wikipediaの記載によると、「奴隷」は「人間でありながら所有の客体即ち所有物とされ、人間としての名誉、権利・自由を認められず、他人の所有物として取り扱われる。所有者の全的支配に服し、労働を強制され、譲渡・売買の対象とされた」とされています(https://ja.wikipedia.org/wiki/奴隷)。
ここでポイントを下記にまとめたいと思います。

① 他者の所有物とされ、人間としての権利を認められない
② 所有者の全的支配に服し、労働を強制される
③ 譲渡・売買の対象とされる

ポイントをざっくりとまとめると主に上記の3点として良いかと思います。①権利(人権)がなく、②労働を強制され、③売買の対象とされる、です。

もう少し考えてみましょう。①の人権については日本国憲法などの「基本的人権」などを参考にして考えて良いかと思います。たとえば、自由権とされる、「自由に物事を考え、自由に行動できる権利」なども基本的人権に含まれています。

②も③も「自由に選ぶ権利がない」というのが入っているので、「奴隷」をざっくりまとめて「選択の自由がない」と解釈してもそれほど異論はないかと思います。ということで、当記事において、「奴隷とは選択の自由がない人」と解釈するものとし、以下論じていきます。
（少し論理展開に飛躍がありますが、あまり前提を詳しくすると話が進まないのでこのようにざっくりと総括しました。）

2. 不確定な状況における「借金」が意思決定範囲を狭める可能性
1節では「奴隷」とは「自由に選ぶ権利がない状況に置かれた人間」という解釈をしましたが、2節ではこの解釈を踏まえて不確定な状況における「借金」が意思決定範囲を狭める可能性について考えてみたいと思います。

少し具体的に考えてみます。たとえば、次の週までに必ず返さないといけない借金がある場合、皆様はどのように考えますでしょうか。「必ず返さなくては」というのも色々とありますが、「返さないことにより大きな不利益」を被る状況です。自宅まで取り立てが来る、などが例としてはわかりやすいでしょうか。身の危険を感じる状況であれば、「なんとしてでもお金を作らなくてはいけない」と考えると思います。

さて、この際に取り得る行動としては「お金を手に入れる」ということですが、株式などの資産を持っていれば売却も可能ですが、ない際は労働が必要になります。ここで労働が問題になってくるのは、稼ぐことができれば良いとして、どう考えても稼げる金額ではない際は非常に厳しい状況に置かれるということです。

これは一個人にとって物凄く厳しくて難しい問題です。何かしらの選択が強いられることでしょう。無理矢理働いて返したり、親戚から借りたり、自己破産したりと人によって様々です。ですが、これらは少なくとも「借金」がなければ行わなくて良い内容になります。

このように「借金」は意思決定範囲を狭めたり何かしらの行動を強いられたりと、ある程度選択の自由を奪います。1節で「奴隷」について確認しましたが、「選択の自由」がある程度狭められていたらマイルドな意味で「奴隷」とみなして良いと思います。ということで、「借金」によって立ち行かなくなると、「奴隷ライク」な状況(準奴隷とも呼ぶことにします)に置かれるようになるとしても良いと思います。

とはいえ、企業などは多かれ少なかれ「借り入れ」を行なっていたり「リスク」を取ることを良しとする風潮があったりもします。では「借りる側」が「借金」すべき時と「借金」すべきではない時はどのように判断するのが良いでしょうか。

一つの判断基準として、「プラスになってリターンが返ってくる見込みがあるか」というのが良いのではと思います。事業投資に回して回収できるならポジティブだし、ただ漫然と借りて使ってしまうのであればネガティブです。逆に言うと、「明確なリターンが不確定」の際の「借金」はあまり良いものではありません。「借金」で「ギャンブル」したり「浪費」したりするのは駄目だという認識は皆それなりに持っていますが、これも「明確なリターンが不確定」だからです。

ですが、皆が堅実な場合、「明確なリターンが不確定」なものに誰も手を出してくれなくなります。こうなると、「準奴隷(奴隷ライクな人)」を作り出すには不都合です。これをどのように解決したら良いのでしょうか。一つの解決策として、「借金」をポジティブに見せる手法があり、これについては3節で取り扱います。

3. 逆に「借金」をいかにポジティブに見せるか
2節によって、「借金」によって相手を追い込むことにより、「準奴隷」を作り出せる可能性について論じてきました。ですが、皆堅実になってしまってはなかなか「奴隷」の多い素晴らしい世界を実現することが難しいです。そこで3節では「逆に借金をポジティブに見せてしまえば良いではないか」ということで「ポジティブな見せ方」について考えていきます。

物事をたとえ良いものでなくても「ポジティブに」見せるにはどうしたら良いのでしょうか。一つの方法が、「名前を変える」です。たとえば、住民サービスを削りたい際にそのまま言っては反対される状況でも、「既得権益の打破のために」と言うだけで賛同者が増えます。同様に、「学業のための借金」と言われたら避ける条件でも、「奨学金」と言われると良いもののように見えます。「コロナに関連する無利子無担保の融資」も、支援としてのポジティブな印象が強いです。しかし、本当に「奨学金」や「コロナ融資」は無条件にポジティブに見て良いものなのでしょうか。

2節では「借りる側」が「借金」すべきかすべきでないかを判断する基準として、「明確なリターンが見込めるかどうか」について記載しましたが、こちらを踏襲します。「奨学金」や「コロナ融資」は本当に「明確なリターン」が見込めるでしょうか。この辺の判断は「自由」に決めても良い反面、結果については「自己責任」だったりします。ですが、借りる際になんとなく「皆借りているようだし...」と流される人は多いのではないでしょうか。

このように、一見評価が難しいことでも「ポジティブに」見せることで、人は警戒を緩める可能性があります。結果として、全員が奨学金を返せているでしょうか、コロナ融資は全企業が返せるでしょうか。もちろんしっかりとしたリターンを得る人もいると思いますが、おそらくは一定比率で無理な人も出てくるかと思います。

ということで、このように名称をポジティブに見せるだけでも、実は意外とリスクのあるタイミングで、「借金」をする人は一定数生じます。これによって奴隷作りの第一段階は突破できるわけです。

4. 過剰供給による「需要と供給」の均衡の崩壊
3節では「ポジティブに借金させる」方法について考えてきたわけですが、奴隷がたくさん欲しい我々上級国民にとっては、一人でも多くの金銭的なやり繰りを破綻させなければなりません。どうすれば良いでしょうか。

一番簡単なのはデフレを作ることです。過剰供給社会においては「需要と供給」の均衡が大きくなり、あらゆる「供給サイド」が弱い立場になります。こうなってくると、「労働」という「供給」自体の本質的な価値も下がります。こうなると、「たまたま良い職に就けなかった」だけで、「奨学金」の返済は難しくなります。また、生活にかかる最低限のコストを可能な限り上げるという手法もあります。消費税を上げるように政治に圧力をかける、家賃を高騰させる(家賃保証会社なども含む)、などやり方は様々です。他にもレジ袋の導入や社会保障の負担額を上げ手取りを減らすなど、様々な手法があります。

さて、このように「借金」を多く抱え、「収入」も上がらない状況が続けば、一定の確率でやり繰りが破綻する人が出てきます。「自己責任」の論調も強いですが、それは「戦術」的な視点であり、「戦略」的な視点ではありません。要は、破綻しやすい状況に多くの人間を一定期間置くだけで、誰かしら破綻してくれます。

一度生計が破綻してしまえば基本的に立て直しが難しいですが、ここで上級国民として気をつけなければいけないのが「窮鼠猫を嚙む」という状況にはしないということです。必ず逃げ道を用意して、「準奴隷」に「自分で決めている」という実感は与えねばなりません。本当に追い詰められると「基本的人権を盾に取った自己破産的な逃げ方」や、「弱者同士の連帯」につながる可能性があります。いわゆる「革命」というのは「弱者同士の連帯」が基盤になりやすいかと思います。本来10選べる手段を望ましくない3つほどに絞るくらいでとどめるというのが長く「準奴隷」を維持するための秘訣です。

ちなみに改憲によって、「基本的人権」をなくしてしまえればもっと良いですが、国民投票で過半数を取るのはなかなか大変です。「少数による多数の支配」があくまで理想なので、過半数に取って都合の良い内容であっては困るのです。「公共の福祉」を「公の秩序」に変えるなどで、うまく権力に都合の良い方向に持って行ったり、「法解釈の変更」や「緊急事態条項」である程度押し切るのも一つの手ですが、世論をうまくコントロールする必要も生じてきます。

5. 奴隷が多い社会の素晴らしさを考える
ここまでは「奴隷の作り方」について考察してきました。最後に、「奴隷社会の素晴らしさ」について上級国民の視点で論じたいと思います。

某漫画に「金は命より重い」という名言がありますが、まさに「金は命より重い」のです。何故ならば「金は命より重いからです」という「循環論法」はさておき、「金が命より重い状況」を作り出すことができれば「奴隷」を作り出すことができます。

このような社会になった際に、上級国民にとって楽園的な世界を実現することができます。どこに行っても人を安く使える、金を払って言う事を聞かせれば良いのです。また、一等地に居を構え、別荘などを保持し、高級食材を独占し、贅沢の限りを尽くせます。なんて素晴らしい世界でしょうか。

ここで記したノウハウが「奴隷イノベーション2.0」の実現に向けてのバイブルとなれば大変幸いですと述べた上で、当記事の締めといたします。

※ 当記事はあくまでも考察であり、筆者の信条を反映させたものではありません。そのため、このように考えられるのではという範囲を超えるものでないことは強調します。