モンテカルロ木探索(MCTS; Monte Carlo Tree Search)の概要
https://www.andrew.cmu.edu/course/10-703/textbook/BartoSutton.pdf
上記のSutton本を読み進めているのですが、Ch.8が若干説明がややこしくなってきて読みづらくなってきたので、関連知識として気になったモンテカルロ木探索(MCTS; Monte Carlo Tree Search)について概要をまとめたいと思います。
主に参考としては上記のWikipediaの記載を参考にしたいと思います。
以下目次になります。
1. モンテカルロ木探索の概要
2. model-based強化学習との関連
3. まとめ
1. モンテカルロ木探索の概要とアルゴリズム
1節ではモンテカルロ木探索の概要とアルゴリズムについてまとめます。

まずはWikipediaの冒頭を確認します。モンテカルロ木探索(MCTS; Monte Carlo Tree Search)は、モンテカルロ法を用いた木の探索のことであるとされています。ヒューリスティクスな探索アルゴリズムとされており、ヒューリスティクスは近似の文脈でも聞く言葉ですがここでは「途中で不要な探索をやめ、ある程度の高確率で良い手を導ける」アルゴリズムであるとされています。モンテカルロ木探索の主要な利用例としては、囲碁やチェス、将棋などが挙げられています。

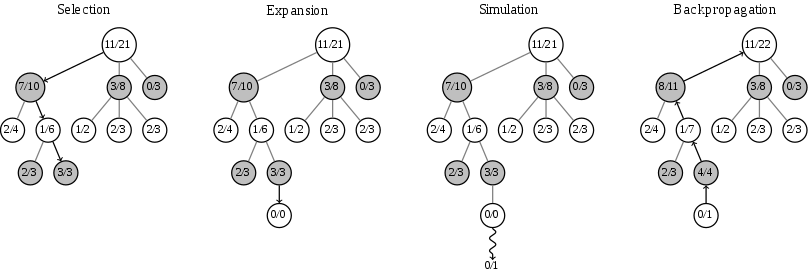
上記は冒頭の図とも同様ですが、モンテカルロ木探索のステップとしては(1)選択(Selection)、(2)展開(Expansion)、(3)シミュレーション(Simulation)、(4)逆伝播(BackPropagation)の4ステップが挙げられています。

それぞれの4ステップは上記のように説明されています。図と見比べながら把握すると良いと思います。

展開で一つ先の局面を作成した後に、シミュレーションでランダムにゲームをプレイングした後、逆伝播で遡って勝敗を記録するとされています。モンテカルロ木探索では計算の制限時間に到達するまでこれを反復し、最も勝率が高い手を選択するとされています。

モンテカルロ木探索の課題としては、子ノードを選択するにあたって、高い勝率であるという知識利用(exploitation)と新たな局面の探索(exploration)のバランスをどのように取るかの点があるとされています。こちらに対する解決策として、UCT(Upper Confidence Tree)やPUCT(Polynomial Upper Confidence Tree)などの手法が提案されています。また、近年話題になった2017年のAlphaZeroはPUCTの手法を改変して用いているとされています。

この中で比較的シンプルなUCT(Upper Confidence Tree)について、上記を元に確認しておきます。UCTでは第1項で知識利用、第2項で探索を表現することで、ノードの探索の優先順位をつけるというアルゴリズムとなっています。
2. model-based強化学習との関連
2節ではmodel-based強化学習に関連付けながらモンテカルロ木探索について確認します。強化学習において環境のモデルを想定するかしないかでmodel-freeとmodel-basedにアプローチが分けられるとされています。

Sutton本のCh.8ではこのmodel-freeとmodel-basedを上記のように表現していました。modelを介して価値や方策を決めるのをplanning、experienceを元にそのまま学習させるdirectRLはlearningとされています。
モンテカルロ木探索では、環境のモデルを仮定した上でプランニングに近い計算を行っていると一旦考えておけば十分そうです。
3. まとめ
今回はWikipediaの記載を元にモンテカルロ木探索について取り扱いました。
Sutton本の記載も含めて大分model-based強化学習については理解が進んできたので、次ステップとしては最近公開されたmodel-basedなアプローチのMuZeroについて確認していければと思います。MuZeroはAlphaZeroなどのように囲碁のようなゲームで高いパフォーマンスを保ったまま、Deep Q-Network系のmodel-freeのアプローチが中心だったAtariのベンチマークを更新しており、現在注目を集めているモデルです。
MuZeroについて確認しながら今回の話は都度振り返られればと思います。