ガウス過程の実装①（動径基底関数カーネルを用いたガウス過程からのサンプリング）｜スクラッチ実装で理解する機械学習アルゴリズム #6

f:id:lib-arts:20190603234751p:plain

連載の経緯の詳細は#1でまとめましたが、本シリーズではあえてスクラッチ実装を元に機械学習のアルゴリズムを実装していくことで、アルゴリズムの概要を掴んだり理論の流れを掴んだりできるようにできればと思います。

実装のほとんどが車輪の再発明に近くなりますが、ベーシックなアルゴリズムをあえて一から自分で追ってみるというのは引き出しを増やすという意味で非常に有意義です。
#2、#3、#4、#5では一般化線形モデル(GLM; Generalized Linear Model)の具体例としてロジスティック回帰やポアソン回帰に対しニュートンラプソン法や勾配法、MCMC法での実装を通して理解を深める手助けとしました。

一般化線形モデル(GLM)の理論と実装①【ロジスティック回帰_前編】｜スクラッチ実装で理解する機械学習アルゴリズム #2 - lib-arts’s diary

一般化線形モデル(GLM)の理論と実装②【ロジスティック回帰_後編】｜スクラッチ実装で理解する機械学習アルゴリズム #3 - lib-arts’s diary

一般化線形モデル(GLM)の理論と実装③【ポアソン回帰編】｜スクラッチ実装で理解する機械学習アルゴリズム #4 - lib-arts’s diary

#6以降では下記の本を最近読んでいて面白かったのでガウス過程について取り扱っていきます。

ガウス過程と機械学習 | 書籍情報 | 株式会社講談社サイエンティフィク

#6では「動径基底関数カーネルを用いたガウス過程からのサンプリング」について解説と実装の紹介を行います。
以下目次になります。

1. 動径基底関数カーネルと共分散行列の計算
2. コレスキー分解と多変量ガウス分布からのサンプリング
3. ガウス過程からのサンプリングの実装
4. まとめ

1. 動径基底関数カーネルと共分散行列の計算
以前の『ガウス回帰と機械学習』の読解メモでも記しましたが、ガウス過程では $\mathbf{y}$ 〜 $N(0,\mathbf{K})$ に従ってサンプルの $\mathbf{y}$ が生成されます。

また、このサンプルの生成にあたって『ガウス回帰と機械学習』の3.2.4で図3.8のように値を生成しているのですが、こちらについて今回は再現していければと思います。
再現にあたって、まず以下で表す動径基底関数(RBF; Radial Basis Function)カーネル
$k(x,x')=\theta_{1}exp(-\frac{|x-x'|^2}{\theta_{2}})$
において $\theta_{1}=1$ 、 $\theta_{2}=1$ を仮定してサンプリングを行います。上記の関数において $(x_{1},x_{2},x_{3},x_{4})=(1,2,3,4)$ を考えた際に共分散行列を計算すると下記のようになります。（実装の解説は後ほど行います）

f:id:lib-arts:20190604000700p:plain
今回はこの共分散行列を元にサンプルの生成を行います。サンプルの生成にあたっては『ガウス回帰と機械学習』の2.3.2で解説されているコレスキー分解を用いる必要があるので、そちらについては2節で取り扱います。

2. コレスキー分解と多変量ガウス分布からのサンプリング
2節ではコレスキー分解とサンプリングの話についてまとめます。1次元データのサンプリングであれば確率密度関数に基づいてデータを生成すれば良いのですが、多変量となるとそうはいきません。多変量でも無相関のデータであれば1次元データと同様に生成できるのですが、相関がある場合は共分散行列を考慮する必要があります。コレスキー分解によって $\mathbf{\Sigma}=\mathbf{L}\mathbf{L}^T$ のように変換できるとすると、
$p(\mathbf{y})=p(\mathbf{L}\mathbf{x}) \propto exp(-\frac{1}{2}\mathbf{y}^T(\mathbf{L}^{-1})^T\mathbf{L}^{-1}\mathbf{y}) = exp(-\frac{1}{2}\mathbf{y}^T\mathbf{\Sigma}^{-1}\mathbf{y})$
上記のようになるので、多変量ガウス分布 $N(\mathbf{0},\mathbf{\Sigma})$ に従うベクトル $\mathbf{y}$ を生成するには、 $\mathbf{x}=(x_{1},x_{2},...,x_{n})$ をランダムに生成して、 $\mathbf{y}=\mathbf{L}\mathbf{x}$ と変換すれば良いです。

3. ガウス過程からのサンプリングの実装
2節までで問題定義やサンプリングについての方針についてまとめたので、3節では実際に実装コードを動かしていければと思います。まず下記を実行してカーネル行列を生成します。

import numpy as np
import matplotlib.pyplot as plt

theta = np.array([1,1])
x = np.array([1,2,3,4])

K = np.array([[1.,2.,3.,4.],[1.,2.,3.,4.],[1.,2.,3.,4.],[1.,2.,3.,4.]])
for i in range(K.shape[0]):
K[:,i] = theta[0]*np.exp(-(K[:,i]-x)**2/theta[1])
print(K)

実行結果は下記のようになります。

f:id:lib-arts:20190604003557p:plain
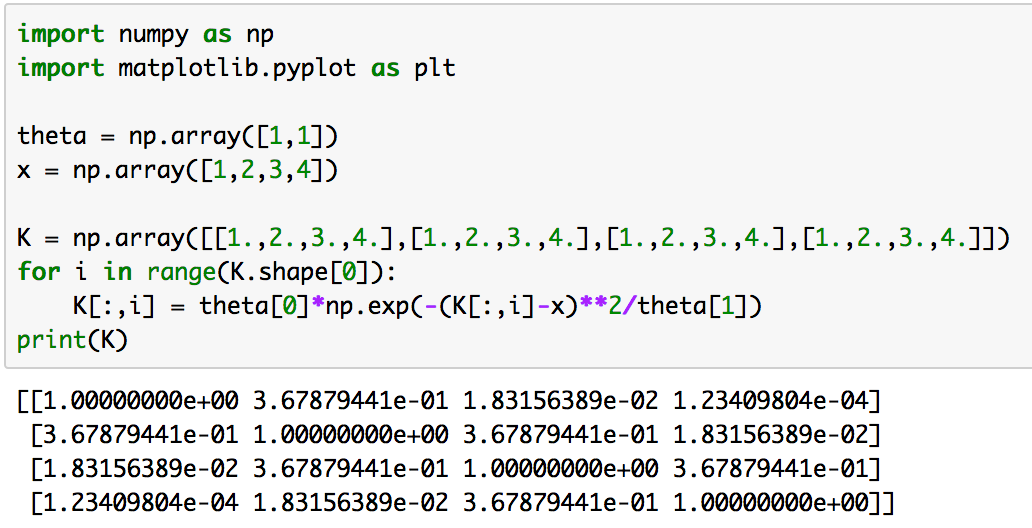
次に下記のコードでコレスキー分解を実行し、サンプルを生成し、プロットを行います。

L = np.linalg.cholesky(K)
np.random.seed(10)

y1 = L.dot(np.random.rand(4))
y2 = L.dot(np.random.rand(4))
y3 = L.dot(np.random.rand(4))

plt.plot(x,y1)
plt.plot(x,y2,color="green")
plt.plot(x,y3,color="red")
plt.show()

実行結果は下記のようになります。

f:id:lib-arts:20190605163038p:plain