微分と最適化｜初心者向け_ディープラーニングの仕組み #1

f:id:lib-arts:20181228181633p:plain

1.1 中学高校数学の復習：微分を使って二次関数の頂点を求める

以下のような問題は中学・高校の頃に解いたことがあるかと思います。

問題

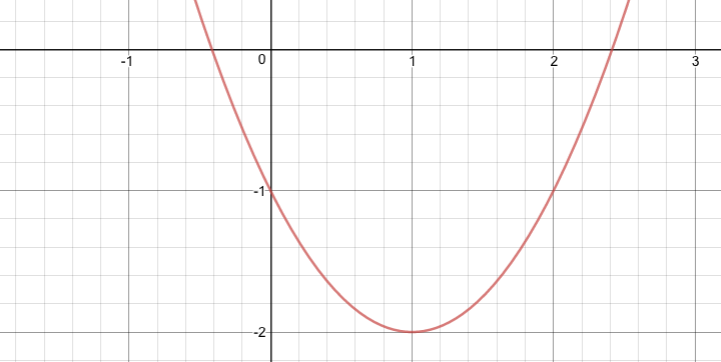
以下の関数f(x)が最小値をとる時のxを、微分を用いて求めてください。

$f(x)=x^2-2x-1$

解答

関数f(x)を微分すると

$f'(x)=2x-2$

となるので、関数f(x)が最小値をとる時は f'(x)=0 をとる時、すなわち

$2x-2=0$
$x=1$

の時に $f(x)$ は最小値をとります。

学生時代、こんなこと勉強してなんの役に立つんだと疑問を持ちながらも鼻をつまんでとっとと解いてた方も多いかと思います。

しかし、この概念こそが機械学習の仕組みを知る上でとても重要なポイントになります。

1.2 これが機械学習にどう役に立ってるの？

このシンプルな問題は機械学習を理解する出発地点として重要な役割を持っています。
それを理解するために機械学習（教師あり学習）が適切なアウトプットを出すために行っている基本的なアルゴリズムを見ていきましょう。

現在機械学習は大きく教師あり学習、教師なし学習、強化学習の３つに分類されることが多く、その中でも教師あり学習は異常検知や画像認識など幅広い技術になくてはならない手法であるといます。今回は具体的にイメージを掴んでいただくために教師あり学習の一番基本的な手法である線形回帰の例に沿って解説します。

教師あり学習の一般的な仕組みは「訓練データ」と呼ばれる一定量のデータセットから私たちが出したいと思っているアウトプットが実際にどのような規則（パターン）で出ているかを学習する「予測モデル」を作ります。そして、その「予測モデル」に「テストデータ」、すなわちまだアウトプットが未知のデータセットを当てはめると、どのようなアウトプットが行われるかを予測することができるというわけです。

（予測モデルの関数を「h」としたのは、このような関数がhypothesis functionと呼ばれることがあるためです Machine Learning | Coursera）

f:id:lib-arts:20181228165647j:plain

例えば私たちがマンションの家賃を予測したいとしましょう。

今回は単純に広さのみで家賃の高さを予測することにします。

例えば「訓練データ」には７件の物件の広さと価格が保持されているとします。

価格をy、広さをxとして散布図に表すと下図のように書けます。

f:id:lib-arts:20181228195839j:plain

直感的に、物件が広ければ家賃が高いというパターンが掴めそうです。

直線を引こうと思えば右肩上がりの直線が引けそうです。家賃の予測値はその直線式に個々の部屋の広さ(x)を代入すれば求められます。これが単回帰による予測の流れです。

しかし、その直線式h(x)の切片と傾きはどのように決めればよいでしょうか。

これは与えられた訓練データを用いた「最小二乗法」によって求めることができます。

下図を使って説明します。

f:id:lib-arts:20181228171829j:plain

散布図の傾向を「直線」で表そうとするとき、どうしても全ての点を完璧に通る直線を引くことはできません。ではどのようにして「最適な」直線を引くかというと、各データと引いた直線との「ギャップ」が最も少ない直線を目指せば良いです。

最小二乗法はこの「ギャップ」を「予測値と実際の値との距離」で表します。

$J = \sum_{i=1}^n (y_i-h(x_i))^2$

距離は絶対値ではなく差の二乗によって表す「ユークリッド距離」を扱っています。（距離の種類については別の記事で説明します。）

この距離の総和(=J)が、最小になるような切片bと傾きaを持つ直線hこそが、「訓練データの傾向を最もよく表した単回帰直線」となります。

関数Jは、関数hの「損失関数」と呼ばれます。

今回の回帰分析による「学習」とは、「損失関数Jが最小値をとるような関数hを求めること」といえます。

その時に使われるのが、先ほど解いたような導関数で最小値を求める計算です！

それでは、実際に手計算で「訓練データから学習した予測モデル」を作ってみましょう。

1.3 最小二乗法を手計算で求めてみよう！

訓練データの値などはスタンフォード大学が提供しているMachine Learning | Courseraで受けることができるweek1のquiz2から拝借しました。

問題

以下のように与えられたデータから、 $h(x)=ax+b$ という予測モデルを考えるとします。最小二乗法を適用した時、aとbはいくつになると考えられるでしょうか？

x	y
1	0.5
2	1
4	2
0	0

解答

これを解く手順は以下の通りです。

xの値をh(x)に代入し、その結果 $h(x)$ をaとbを使って表す
同様に $(y-y~)$ 、 $(y-h(x))^2$ をaとbで表す
$(y-h(x))^2$ を全て足しあげる（これで損失関数Jをaとbで表せる）
関数Jが最小値をとるようなaとbを偏微分式を使って求める

1、2までの値を求めると、以下の表になります。

x	y	h(x)	(y-h(x))	(y-h(x))^2
1	0.5	a+b	0.5-(a+b)	$0.25-(a+b)+(a+b)^2$
2	1	2a+b	1-(2a+b)	$1-2(2a+b)+(2a+b)^2$
4	2	4a+b	2-(4a+b)	$4-4(4a+b)+(4a+b)^2$
0	0	b	-b	$b^2$