簡単な数式で理解する回帰分析の学習の流れ｜高校数学の演習を通して理解するニューラルネットワーク #4

f:id:lib-arts:20181228181633p:plain

当連載は、高校数学の演習を通して機械学習のアルゴリズムの一つであるニューラルネットワークを理解しようというものです。連載の経緯につきましては#1にまとめましたので下記をご覧ください。

簡単な6題の例題をもとにニューラルネットワークの仕組みに現れる基礎的な数学についてフォーカスします。
#1~#3では6題の例題に関して取り扱いました。

#4、#5ではこれまで行った例題の解説の内容を踏まえて、回帰分析の学習の流れの理解からニューラルネットワークへの理解へと繋げていきます。
以下、目次になります。

1. 例題6題の振り返り・総括
2. 回帰分析の学習の流れ
2.1 モデルの数式の定義
2.2 誤差関数の定義
2.3 最適化
3. まとめ

1. 例題6題の振り返り・総括

例題の詳細に関しては#1~#3にまとめていますのでそちらをご確認ください。

6題を振り返ると、ex.01が関数でした。機械学習のアルゴリズムはデータから規則(モデル)を構築するのですが、ニューラルネットワークではこの規則を関数の形で記述します。そのため、関数の考え方が重要になります。

次にex.02が微分、ex.03が微分を用いた最小値問題でした。この後2節でまとめますが、関数近似系の機械学習においては数式を未知のパラメータ（モデルのパラメータ）を用いて定義し、その良し悪しを判断するにあたって誤差関数（評価の指標）を定め、その値の最小とするパラメータを探すという問題に帰着します。この際に関数の傾きの値を利用し、パラメータの値を決めにいきます。

その後のex.04は勾配降下法を用いて最小値（最適化）問題を解きました。ex.03のような傾きが0の点を求めるという手法は方程式が解けることを前提としているのですが、#5で解説するようなニューラルネットワークの関数は複雑でそのまま解くのが困難です。そのため、勾配（各方向の微分の値をベクトル化したもの）を用いて近似的に最適化を行うのが勾配降下法です。

ex.05とex.06は行列の積算とそれをMLP(MultiLayer Perceptron)のようなニューラルネットワークの推論との関係について取り扱いました。こちらに関しては#5で回帰分析の数式の拡張として取り扱います。

以上で、#1~#3の振り返りと#4、#5への導入についてまとめられたので、#4では単回帰分析をベースにした学習の流れ、#5では回帰分析の数式の拡張について諸々取り扱っていきます。

2. 回帰分析の学習の流れ

2節では回帰分析の学習の流れについてまとめていきます。

f:id:lib-arts:20181228195839j:plain

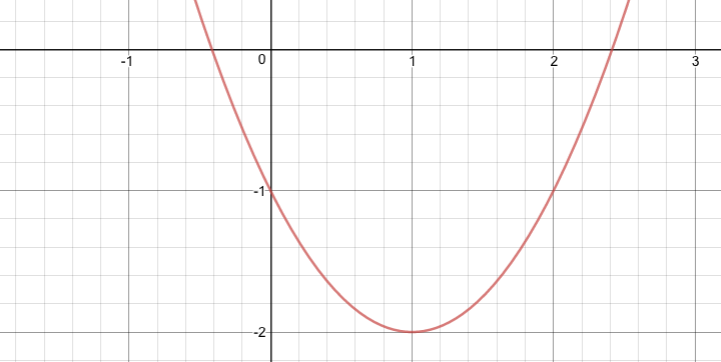
まず前提知識として、回帰分析では上図のような点が与えられた時にxからyを予測する関数を求めます。一旦簡易化のために直線式（一次関数）を前提とします。*1

上記の前提に基づいて一次式でxとyの関係性を近似すると、 $y=ax+b$ という式で近似することができます。この際に近似した $y=ax+b$ を求めることを学習、数式を元に新しいxに対するyの予測を出すことを推論と呼んでいます。この二つのステップは機械学習において重要なポイントなので必ず抑えておいてください。

さて、ここで学習と推論を数学的に考えると推論はxに値を代入するだけなので非常に簡単です。一方で最適なパラメータaとbを求める学習とはどのように行っているのでしょうか。これを解くにあたってex.01~ex.04までの例題で取り扱った内容が役にたちます。具体的にはこの後の2.1〜2.3で解説します。

2.1 モデルの数式の定義

回帰分析の学習（前節で言うならパラメータa,bの推定）にあたっては大まかに分けて3つのステップを踏みます。まず1ステップ目としてモデルの数式を定義します。

具体的には前節で述べたように近似したい関係性を $y=ax+b$ のような数式で表現することです。ここで注意したいのが、問題の定義にあたってはxの値を元にyの値を予測すると言う数式になっているということです。ここでaとbは仮置きしているので任意の実数を取るとします。

とにかく意識したいのが入力した値(x)を元に何らかの値(y)を予測する問題になっているということです。

2.2 誤差関数の定義

2.1ではモデルの数式を定義しました。これによって式の形（単回帰分析では一次関数）を決めることができました。

2.2では $y=ax+b$ のパラメータa,bを決めるにあたって誤差関数を定義します。誤差関数はモデル（ここではパラメータaとbの値）の良し悪しを決める評価の指標で、設定の仕方は様々ですがモデルを介した予測値と実測値の値が近づくと小さくなるように設定します。

ここではシンプルで教科書などで最もよく用いられている最小二乗法（Least-square method）に基づいて説明します。最小二乗法ではモデルの予測値のy（予測値を強調するにあたって以下 $\hat{y}$ と表記します）と実測値の差の二乗を $E(θ) = \sum_{k=1}^{n}(\hat{y_{k}}-y_{k})^2$ のような二乗誤差関数として定義します。ここでEは誤差関数、θは誤差関数のパラメータでここではaとbを表すとします。また、nは観測されたサンプル数、kは観測された各サンプルとします。

この時、 $\hat{y}$ は直線 $y=ax+b$ 上の点なので、 $\hat{y_{k}}=ax_{k}+b$ と表記できます。これにより誤差関数は $E(θ) = E(a,b) = \sum_{k=1}^{n}(ax_{k}+b-y_{k})^2$ と表記できます。 $(x_{k},y_{k})$ は観測されたデータとして与えられるので定数と見做すことができるため、Eをaとbに関して最小化をはかれば良いことがわかります。逆に言うとE(a,b)を最小化するaとbを求める問題であり、Eは評価の指標なのでaとbを最小化するaとbはデータにあてはまりの良いモデルのパラメータとなります。

上記で定義したEを2.3節でaとbに関して最小化（最適化）を行っていきます。

2.3 最適化

2.2で定義した誤差関数の $E(θ) = E(a,b) = \sum_{k=1}^{n}(ax_{k}+b-y_{k})^2$ の最適化（最小化）について2.3節では見ていきます。ここでの最適化を考えるにあたって思い出したいのがex.03とex.04です。これらは関数の最小値問題を二つの見方で解いていました。

・ex.03のような解き方（微分＝０を解く）

まずはex.03の解き方を見ていきます。これを考えるにあたってはE(a,b)の偏微分を考えると良いです。急に偏微分が導入されて難しいかもしれませんが、一旦はaとbのそれぞれの方向に関しての微分だと考えれば良いです。そのため、aの偏微分を考える際はbは定数とみなし、bの偏微分を考える際はaは定数と見なせば良いです。

したがって $\frac{\partial E(a,b)}{\partial a}=0$ と $\frac{\partial E(a,b)}{\partial b}$ の連立方程式を解けば良いです。（詳細の導出は難しいのでここでは省きますが、線形回帰問題ではこの方程式は解くことができ正規方程式と呼ばれています。）イメージとしては山の頂上を探すにあたって、x方向とそれに直角なy方向のそれぞれの傾きが0のポイントを探しているイメージです。

・ex.04のような解き方（勾配降下法）

勾配（各方向の傾き）を用いて解いていくこともできます。ex.04で触れた勾配降下法(Gradient Descent)の内容を元に、 $a_{n+1} = a_{n} - α\frac{\partial E(a,b)}{\partial a_{n}}$ と $b_{n+1} = b_{n} - α\frac{\partial E(a,b)}{\partial b_{n}}$ を用いてaとbを繰り返し演算で近似的に求めていくことで最適なaとbの値を求めることができます。