指数関数・三角関数とオイラーの公式|オムニバスでまとめる大学数学 #4
当シリーズは大学数学をオムニバス形式で取り扱っていきます。
#1、#2では解析学の歴史について取り扱いました。
#3では複素解析(complex analysis)の概要について取り扱いました。
https://lib-arts.hatenablog.com/entry/math_la3
#3が概要中心となってしまったため、#4では具体的なトピックとしてオイラーの公式について取り扱います。
以下のWikipediaの記事をベースにまとめていきます。
以下、目次になります。
1. オイラーの公式の概要
2. 指数関数と三角関数の級数展開による簡単な証明
3. まとめ
1. オイラーの公式の概要
1節ではオイラーの公式(Euler's formula)の概要について取り扱っていきます。オイラーの公式は指数関数と三角関数の間に成り立つ公式で、下記のように表すことができます。
ここでeは指数関数、iは虚数単位、cos,sinはそれぞれ余弦関数および正弦関数であることに注意です。オイラーの公式は任意の複素数に対して成り立つ等式ですが、特に
が実数である場合が重要でありよく使われます。
が実数のとき
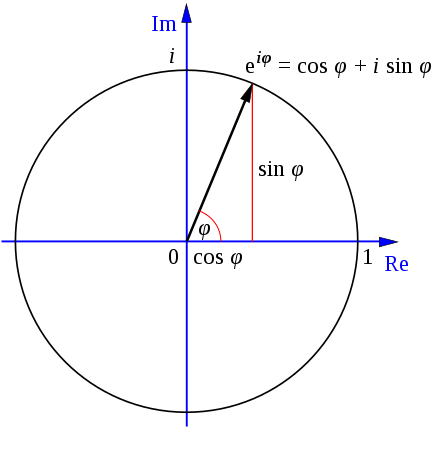
は複素数
がなす複素平面上の偏角(角度
の単位はラジアン)に対応するとされています。

上記はが実数の時のオイラーの公式の図形的な表現となります。
オイラーの公式は複素解析をはじめとする純粋数学の様々な分野や、微分方程式の解析において重要な役割を演じます。物理学者のリチャード・ファインマンに、「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」 だと評されています。
また、オイラーの公式は、変数のが実数である場合には、右辺は実空間上で定義される通常の三角関数で表され、虚数の指数関数の実部と虚部がそれぞれ角度
に対応する余弦関数cosと正弦関数sinに等しいことを表すとされています。
や
などで表すと便利そうです。
ここまでの内容でオイラーの公式の概要についてつかむことができたので1節はここまでとします。
2. 指数関数と三角関数の級数展開による簡単な証明
1節ではオイラーの公式について取り扱いましたが、これが成り立つことはどのように考えていれば良いのでしょうか。公式のイメージを掴むにあたっては証明から再構成するのもヒントになりうるので2節は級数展開による簡易的な証明を見ていきます。厳密さよりも、イメージを掴めるようにというのを優先します。
まず、指数関数、余弦関数(cos)、正弦関数(sin)のマクローリン展開を行います。
ここで、の
を
に置き換え、
の冪級数が絶対収束するために級数の項の順序を任意に交換可能である事を考慮すれば下記が成り立ちます。
この式と三角関数の冪級数展開を比較すれば、オイラーの公式であるを得ることができます。
3. まとめ
#4では複素解析の簡単な具体例としてオイラーの公式について取り扱いました。
#5では今回の導出に用いたマクローリン展開について取り扱っていければと思います。