複素解析のイメージや概要を掴む|オムニバスでまとめる大学数学 #3

当シリーズは大学数学をオムニバス形式で取り扱っていきます。
#1、#2では解析学の歴史について取り扱いました。
#3では19世紀以降の解析学で本格的に利用されるようになってきた複素解析(complex analysis)について取り扱います。
以下のWikipediaの記事をベースにまとめていきます。
以下、目次になります。
1. 複素解析の概要と歴史
2. 複素関数
3. 正則関数
4. 著しい特徴
5. まとめ
1. 複素解析の概要と歴史

複素解析(complex analysis)の概要としては、Wikipediaには上記のように記述されています。「複素数の関数に関わる微分法、積分法、変分法、微分方程式論、積分方程式論の総称」とされています。「現代数学の基礎が複素数であることから、単に解析といえば複素解析を意味することもある」ともされています。また応用分野としては多くの分野が挙げられています。
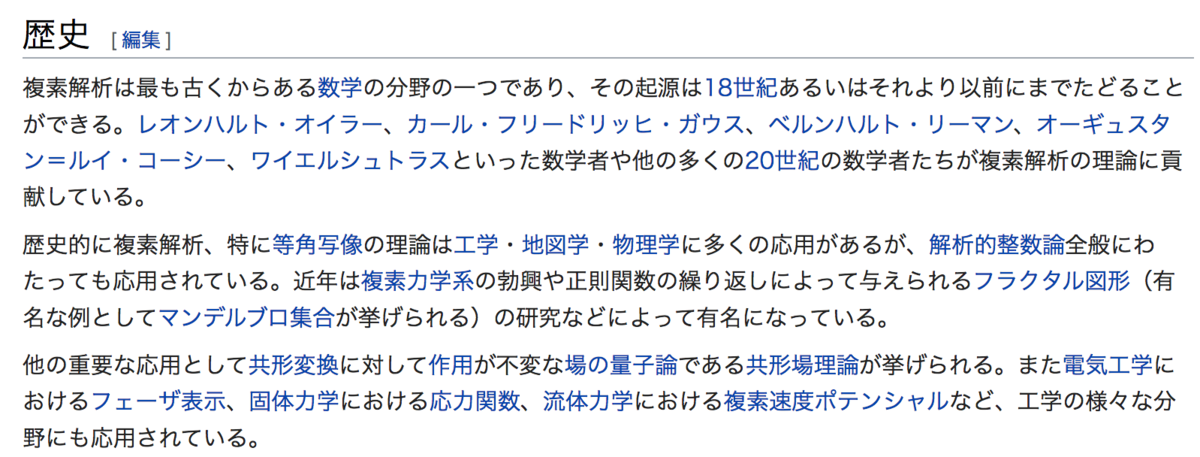
また、歴史としては上記のように記述されています。起源は18世紀もしくはそれ以前とされており、オイラー、ガウス、リーマンなどの有名な数学者の名前が挙げられています。また、20世紀の数学者も複素解析の理論に貢献したとされています。
応用としては、等角写像、フラクタル図形(マンデルブロ集合)、共形場理論、フェーザ表示、応力関数、複素速度ポテンシャルなど様々な応用が挙げられています。

Wikipediaの記述では上記のように書かれています。定義は数式を元に掴んでおくと良さそうです。
上記が2つの実変数、
についての実数値関数だと考えることができる点はなかなか面白いと思います。
のように基本的には実部と虚部にわかれて考えることができるというのにも関連しているかと思われます。
また、複素解析の基本的な概念が「指数関数、対数関数、三角関数などの実関数を複素関数に拡張することにより与えられることが多い」という記述は非常に興味深いです。
有名どころだと上記で表されるオイラーの公式などもこの例であると思われます。
ここまでで大体の内容がつかめたので、3節では正則関数について確認します。
3. 正則関数
3節では正則関数について取り扱っていきます。

上記では正則関数の概要がまとめられています。全体的に興味深い内容ですが、複素関数が定義域全体で複素微分可能というのが定義のようです。また、複素解析においては正則関数(holomoorphic function)、複素微分可能関数(complex differentiable function)、解析関数(analytic function)という用語が同義になることや、複素関数が複素微分可能でない点を特異点(singularity)というなどは押さえておくと良さそうです。

また、上記では複素関数の分類について言及されています。「複素関数が微分可能であるということは、実関数が微分可能であることに比べて遥かに強い条件である。一階微分可能な複素関数は無限階微分可能であり、積分可能であり、解析的である。」というのは意識しておくと良さそうです。
4. 著しい特徴
4節では著しい特徴と記述されているトピックについて取り扱います。

上記がWikipediaでの記載になります。複素解析によく用いられる道具立ての複素線積分において、コーシーの積分定理を用いることにより様々な洞察が得られるようです。また、カゾラーティ・ワイエルシュトラスの定理を用いることで特異点の周りでの関数の挙動はテイラー級数に類似のローラン級数で記述することができるとされています。
三点目としてはリウヴィルの定理によって複素平面全体で誘拐な正則関数は定数関数に限られることがわかるとされています。最後に四点目としては、「正則関数の重要な性質に、正則な関数の連結な領域上全体での挙動が任意のより小さい領域上の挙動によって決定されてしまう(一致の定理)」について言及されています。
ここまでの結果は全て一変数の複素解析であるものの、多変数複素解析に関しても豊かな理論が存在するとされています。
5. まとめ
#3では複素解析について取り扱いました。今回もWikipediaをなぞりながらキーワードを追うのが中心となってしまいましたが、言葉のマッピングがなんとなくつかめれば大体のつながりが見えるようになってくるので、新しい学習をする際の有効なアプローチであると考えています。
#4ではもう少し初歩的な複素解析について取り扱えればということで、オイラーの公式について見ていきたいと思います。