Pythonで実装する関数と微分|Pythonで実装する高校数学 #1

高校レベルの数学は数多くの理工系の分野の基本となり、しっかり理解していると理解していないでは応用力において大きな差がつく分野です。近年流行りの機械学習分野以外でも技術系の多くの専門分野では高校数学の内容を履修していることが必須になります。
とはいえ、どこかで躓いてしまい、そのまま放置としてしまったという方もおられるのではないでしょうか。そのため当シリーズでは高校数学をテーマにしていければと思います。
一方で、数式の羅列だといまいちイメージしにくいというところではあると思うので、当シリーズではPythonで高校数学の内容を実装しながら理解していければと思います。
#1では微分などの分野を行う際にも重要となってくる関数の中から、多項式関数と三角関数について取り扱いたいと思います。
以下目次になります。
1. 関数とは
2. 多項式関数の概要と実装
3. 三角関数の概要と実装
4. まとめ
1. 関数とは
1節では関数の概要についてまとめます。関数という言葉は様々な数学の分野で出てくるだけでなく、プログラミングなどでも関数という言葉が出てくるなど、非常に応用範囲の広い言葉です。ちなみに数学の関数もプログラミングの関数も一見違うようにも見えますが、同じ意味で使用されています。
以下Wikipediaの関数の論述を参考にしていきます。

Wikipediaでは上記のように概要が記述されています。「ある変数に依存して決まるあるいはその対応を表す式」や、「数の集合に値をとる写像の一種」などと難しい記述が並んでいますが、具体的にいえばにおいて、xに1を代入するとyは2になるなど数の対応を表していると捉えると良いです。この対応の規則のことを
と定義していると考えることができます。

横軸で表すxと縦軸で表すy()の対応について上記のように図式化することもできます。上記では
を-5〜5の区間でグラフを描いています。

またこの関数をもう少し抽象化すると上記のようにという関数に入力xを与えて出力の
を得るなどのように図式化できます。この関数の考え方はプログラミングにおける関数の考え方に非常に似ています。
ここまでで大体の関数の概要についてつかめたと思いますので1節はここまでとします。2節、3節では関数の具体例としてそれぞれ、多項式関数と三角関数について取り扱います。
2. 多項式関数の概要と実装
1節では関数の概要について説明したので、2節では関数の具体例として多項式関数を取り扱います。多項式関数は一次関数、二次関数を含む、数学において最初に履修する関数で非常に馴染み深いものです。
まずはWikipediaの記述を元に概要を把握します。

多項式函数 - Wikipedia
上記の記述は少々難しいですが、と考えても良いです。
において
の際は
となるので定数関数、
の際は
となるので一次関数、
の際は
となるので二次関数となります。
ここまでの記述で数式の形や定数関数、一次関数、二次関数についてわかったので、以下は実装を用いて多項式関数を可視化していきます。
・定数関数
まずは定数関数について取り扱います。
import numpy as np
import matplotlib.pyplot as plta0 = 1
x = np.arange(-5,5,0.1)
y = x*0 + a0plt.plot(x,y)
plt.show()
上記を実行すると下記のようになります。
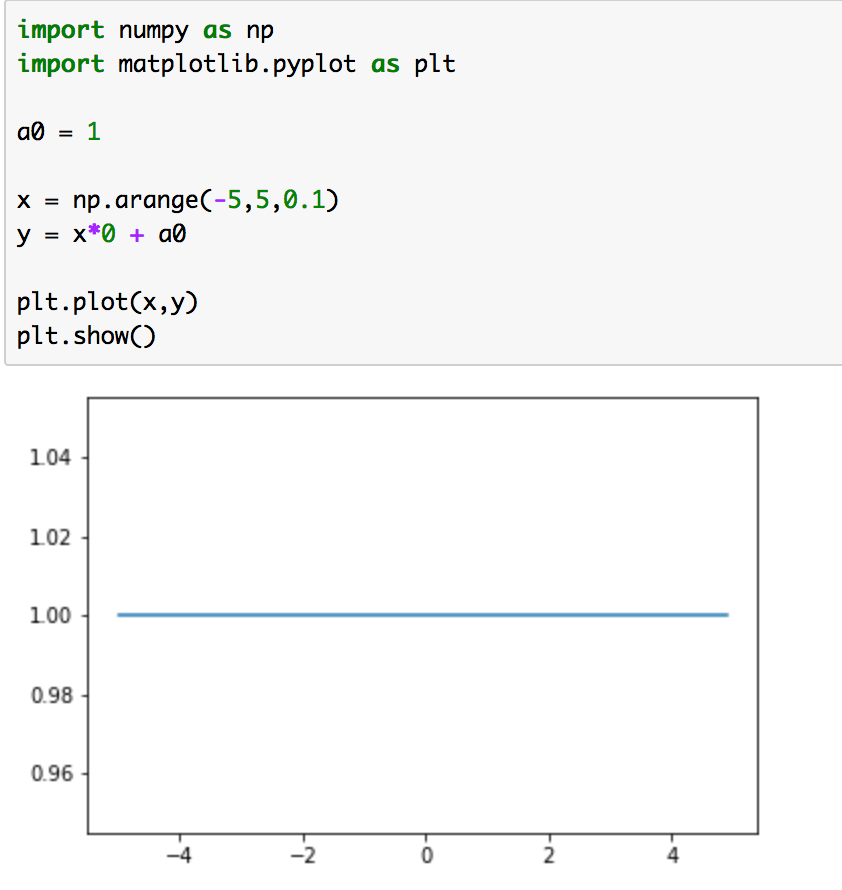
ここで実行コードにおいて"y = x*0 + a0"としたのは単に配列の形を揃えるためなので深い意味はありません。
・一次関数
次に一次関数について取り扱います。
import numpy as np
import matplotlib.pyplot as plta0 = 1
a1 = 1
x = np.arange(-5,5,0.1)
y = a1*x + a0
plt.plot(x,y,label="a0=1, a1=1")
a0 = -1
a1 = 2
x = np.arange(-5,5,0.1)
y = a1*x + a0
plt.plot(x,y,label="a0=1, a1=1")plt.legend()
plt.show()
上記を実行すると下記のようになります。
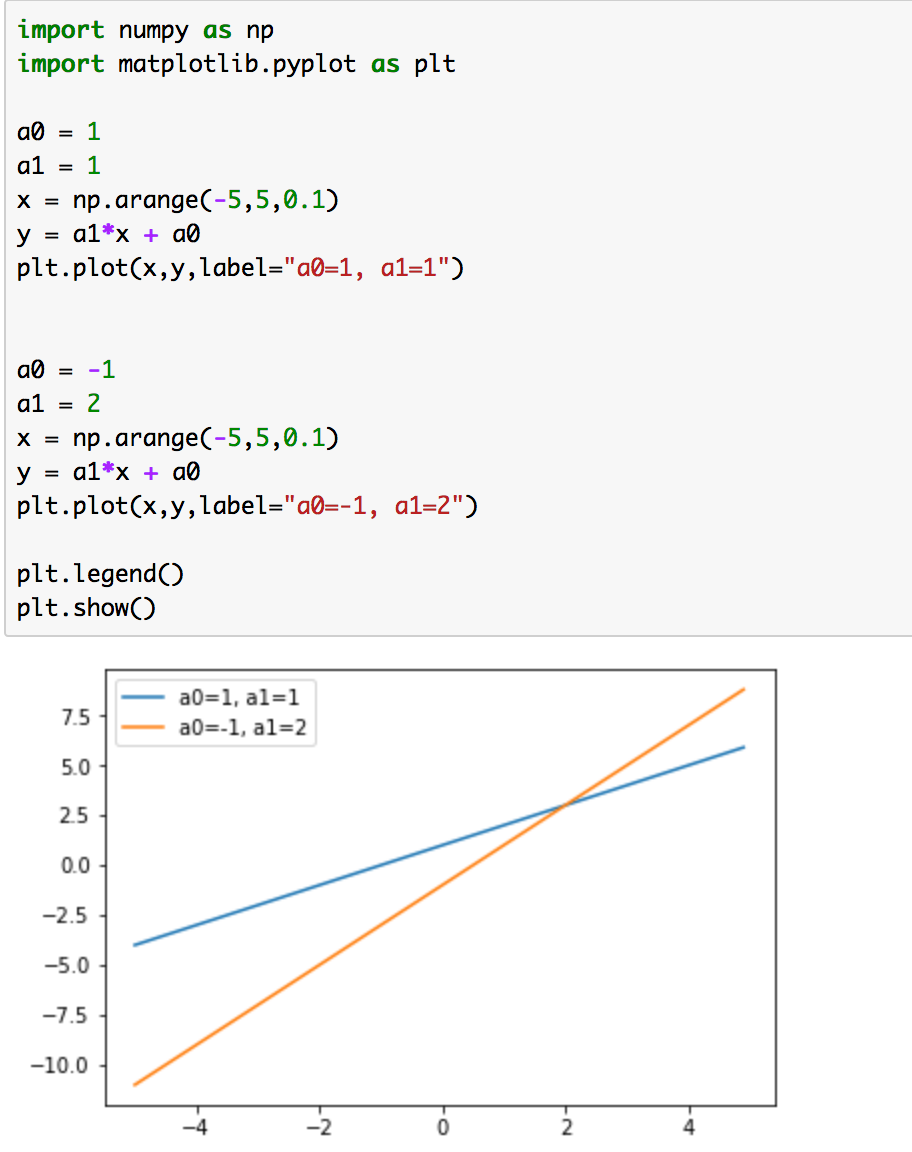
二つの直線を見比べることで、a1が傾きを表しており、a1の値によって関数の上昇度合いが変化することが読み取ることができます。
・二次関数
次に二次関数について取り扱います。
import numpy as np
import matplotlib.pyplot as plta0 = -9
a1 = 0
a2 = 1x = np.arange(-5,5,0.1)
y = a2*x**2 +a1*x - a0plt.plot(x,y)
plt.show()
実行結果は下記のようになります。
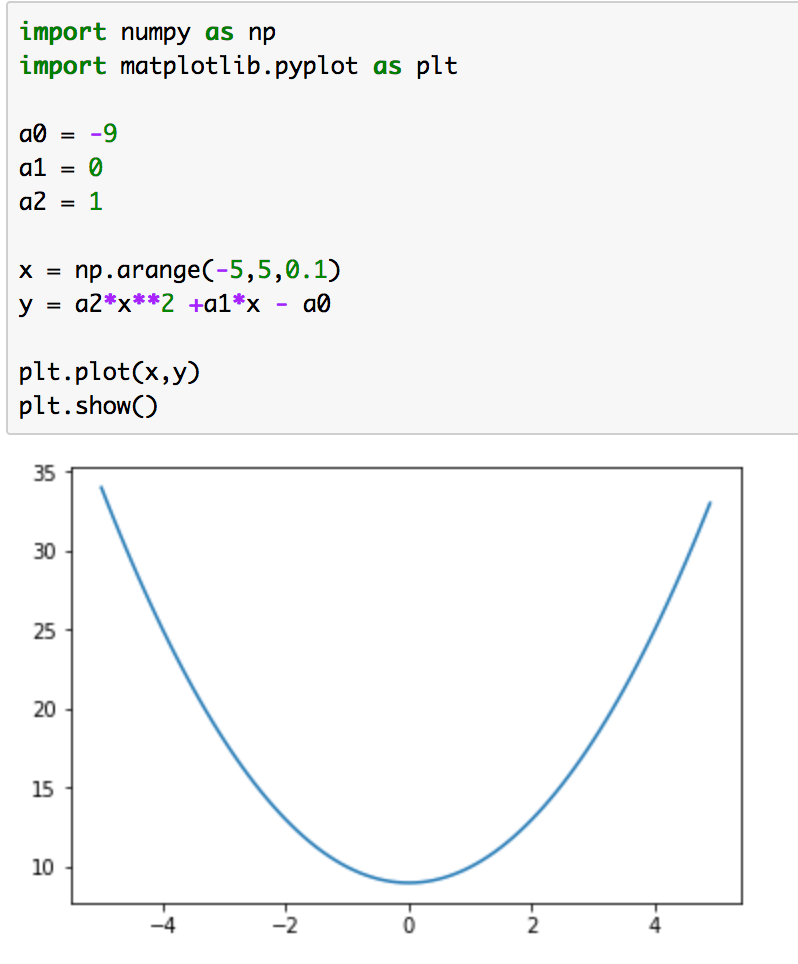
多項式関数については大体のイメージがつかめたと思うので2節はここまでとします。
3. 三角関数の概要と実装
3節では三角関数について取り扱っていきます。三角関数は周期性を持つ関数であることが特徴で、波や電気信号など様々な分野で応用されている関数です。
まずはWikipediaの記述を元に簡単な概要を確認します。

三角関数 - Wikipedia
上記によると、三角関数は「角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称」とあります。また三角関数としては、sin、sec、tan、cos、csc、cotの6つが挙げられています。この中でも高校数学のレベルで特に重要なのが、sin(正弦)とcos(余弦)です。この記述だけだとわかりづらいので図を参照します。

この図を用いることでsinとcosの定義が把握しやすくなります。角Aの角度をとおくと、
と
は下記のように記述できます。
ここまでで大体の定義は確認できたかと思うので、実際にPythonで実装しながらsinとcosを確認します。
下記でsinとcosの値の挙動を確認することができます。
import numpy as np
import matplotlib.pyplot as pltx = np.arange(0,6.28,0.02)
y_sin = np.sin(x)
y_cos = np.cos(x)plt.plot(x,y_sin,label="sin")
plt.plot(x,y_cos,label="cos")
plt.legend()
plt.show()
実行結果は下記となります。
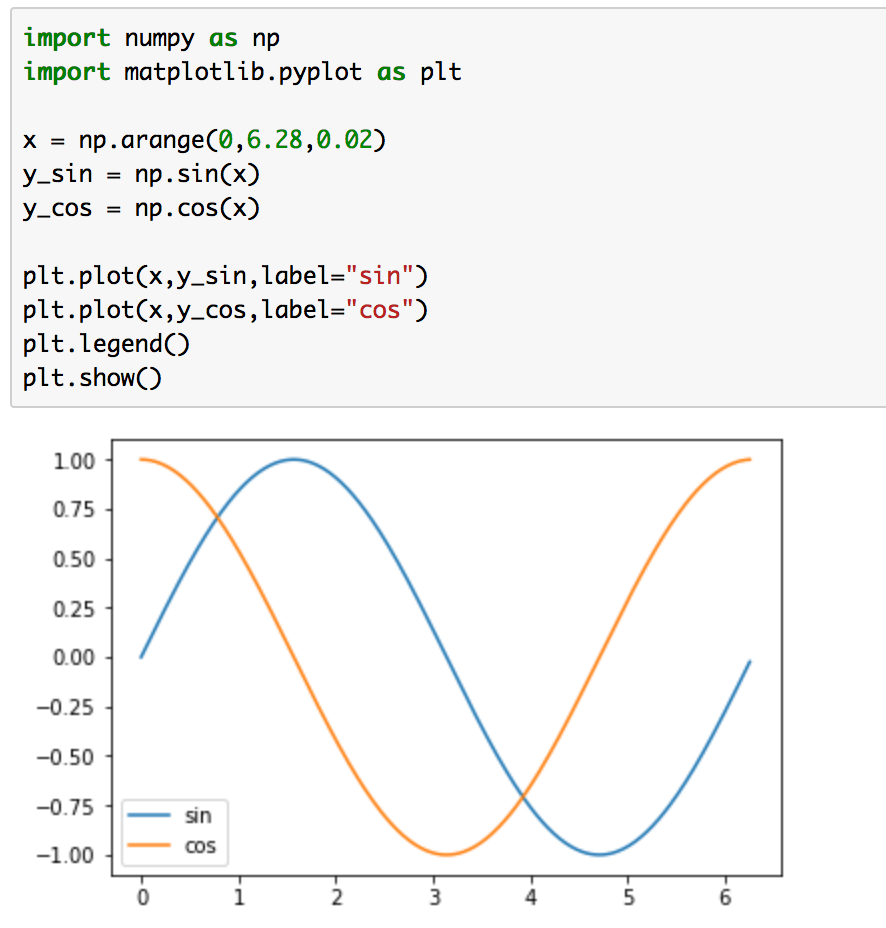
xの値を0〜6.28としているのは、円周率の約2倍という理由があります。三角関数は円周率の2倍である刻みで周期的に同じ結果をとります。また、cosとsinは基本的に同じ形をしていますが、スタート位置が異なっていることに注意です。
ここまでで三角関数の中でもベーシックでよく用いられるsinとcosについて簡単な概要と実装については取り扱えたので、3節はここまでとします。
4. まとめ
#1では多項式関数と三角関数の概要と実装について取り扱いました。
#2では同様に様々な関数を取り扱えればということで、指数関数と対数関数について取り扱います。