Python実装で理解するラプラシアン行列(Laplacian matrix)の概要

f:id:lib-arts:20200215191644p:plain

GNN(Graph Neural Network)関連についていくつか見ていたのですが、ラプラシアン行列はConvolutinal Graph Neural NetworkのSpectral-basedの話に関連して出てくるものの、あまり見たことがなかったのでPython実装を通して簡単にまとめておきます。

[1901.00596] A Comprehensive Survey on Graph Neural Networks

上記のConvolutinal Graph Neural Networkにおいて、正規化ラプラシアン行列(normalized Laplacian matrix)も用いられていますが、概要を掴むのも兼ねてPythonを用いて簡単に実装してみます。
以下目次になります。
1. ラプラシアン行列の概要
2. ラプラシアン行列の実装
3. まとめ

1. ラプラシアン行列の概要
1節ではラプラシアン行列の概要についてまとめます。

f:id:lib-arts:20200215191725p:plain

ラプラシアン行列 - Wikipedia
上記はWikipediaのラプラシアン行列の冒頭部の記載になります。グラフ理論の数学的分野における考え方で、グラフの行列表現を表すとされています。
$\mathbf{L}=\mathbf{D}-\mathbf{A}$
ここで、数式な定義としてはラプラシアン行列の $\mathbf{L}$ は上記のように、グラフの次数行列の $\mathbf{D}$ から隣接行列の $\mathbf{A}$ を引いた行列として定義されています。

f:id:lib-arts:20200215192517p:plain

具体的な値に関しては上記のように、 $L_{i,j}$ が与えられるとされています。 $i=j$ のとき、 $L_{i,j}$ は頂点 $i$ の次数に一致、 $i \neq j$ の際は頂点 $i$ と $j$ が隣接していれば $-1$ に一致、 $i \neq j$ で $i$ と $j$ が隣接していなければ $0$ に一致するとされています。
同様にConvolutinal Graph Neural NetworkのSpectral-basedに出てくる正規化ラプラシアンについても確認しておきます。

f:id:lib-arts:20200215193151p:plain

正規化ラプラシアンは上記のように記載されています。ラプラシアン行列がノード(頂点)の次数で正規化されたと考えておけば良さそうです。 $deg(v_{i})$ や $deg(v_{j})$ は二つのノードが隣接している前提であれば最小値 $1$ を取り、この時 $-\frac{1}{\sqrt{deg(v_{i})deg(v_{j})}}$ は最小値 $-1$ を取ります。 $deg(v_{i})$ や $deg(v_{j})$ は頂点 $i$ と $j$ が他のノードと多く連結していればしているほど値が大きくなるので、-1≦ $-\frac{1}{\sqrt{deg(v_{i})deg(v_{j})}}$ <0の値を動くとだけ把握しておくと良さそうです。
正規化ラプラシアンまで把握できたので1節はここまでとします。

2. ラプラシアン行列の実装
2節ではPythonを用いたラプラシアン行列の簡単な実装を行います。

import numpy as np

a = np.array([[0,1,0,0,1,0],[1,0,1,0,1,0],[0,1,0,1,0,0],[0,0,1,0,1,1],[1,1,0,1,0,0],[0,0,0,1,0,0]])
d = np.diag(np.sum(a,axis=0))
l = d-a

print(a)
print("===")
print(d)
print("===")
print(l)

上記はトップ画像にも貼っているWikipedia記載のラプラシアン行列の実装での表記になります。実行結果は下記のようになります。

f:id:lib-arts:20200215200924p:plain

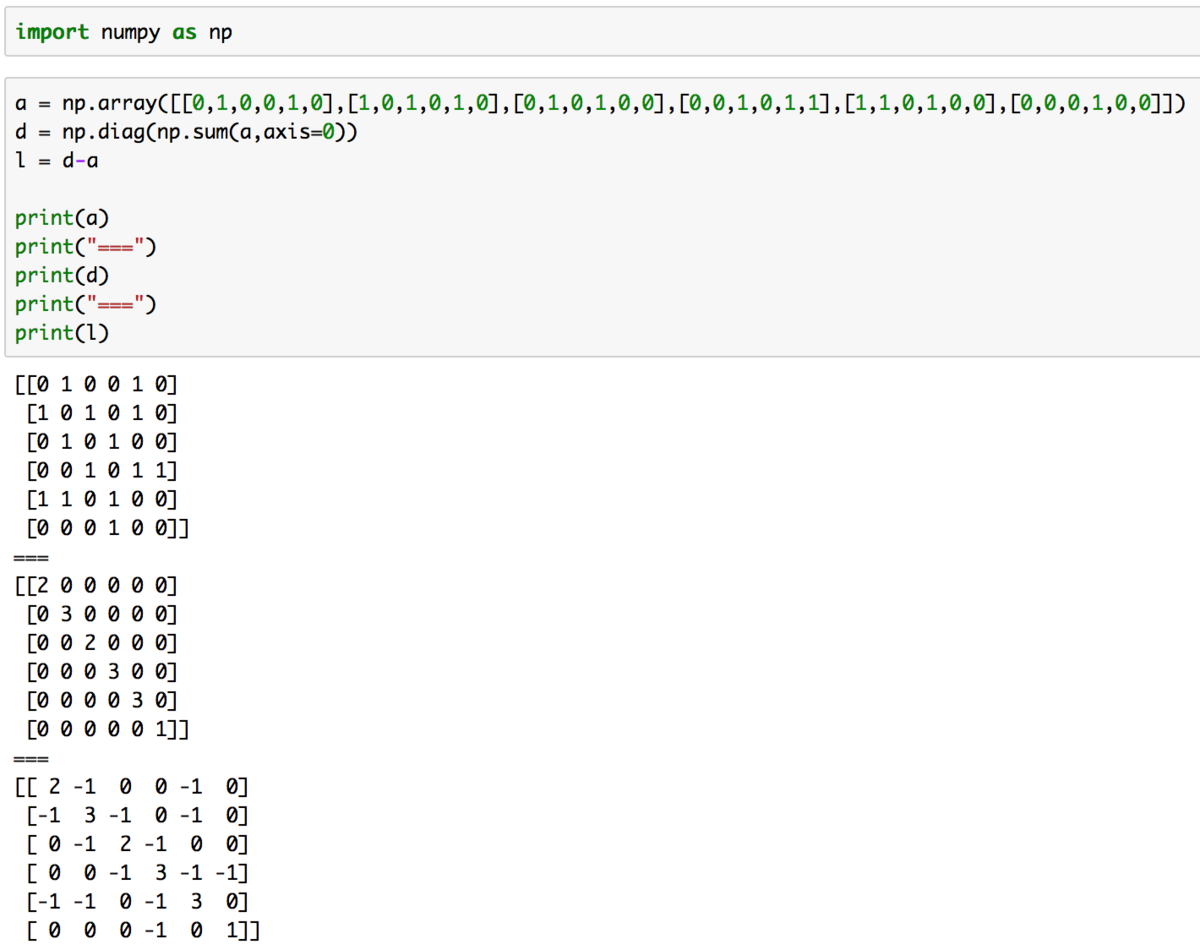
次に正規化ラプラシアン行列について確認してみます。

import numpy as np
from scipy import linalg

a = np.array([[0,1,0,0,1,0],[1,0,1,0,1,0],[0,1,0,1,0,0],[0,0,1,0,1,1],[1,1,0,1,0,0],[0,0,0,1,0,0]])
d = np.diag(np.sum(a,axis=0))
l = d-a

l_norm = np.dot(np.sqrt(linalg.inv(d)),np.dot(l,np.sqrt(linalg.inv(d))))
np.set_printoptions(precision=3)
print(l_norm)

上記の実行結果は下記になります。

f:id:lib-arts:20200215202609p:plain

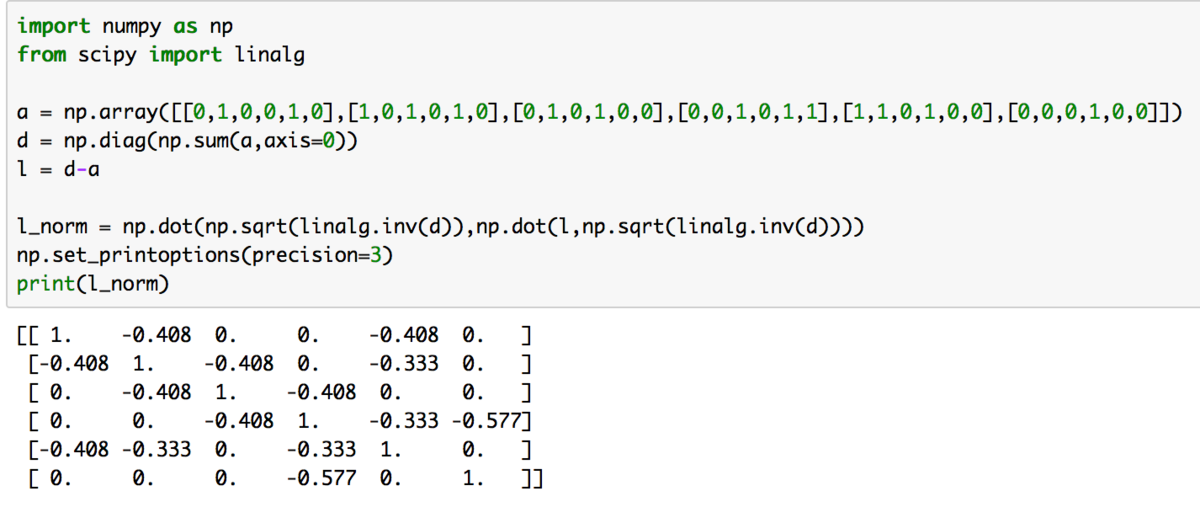
ここでは逆行列の計算としてscipy.linalg.inv、-1/2乗の計算としてはnp.sqrtを用いました(対角行列で結果だけざっくり確認できれば良いという前提だったため、最適な実装ではないかもしれません)。
1節で確認した数式通りの結果が得られ、大枠については確認できたので2節はここまでとします。

3. まとめ
当記事ではGNNで出てくる正規化ラプラシアン行列について取り扱いました。
行列の積などが色々と出てきて複雑そうに見えますが、ラプラシアン行列では $\mathbf{D}$ が対角行列だったため、計算上は比較的取り扱いやすい内容でした。