2021-06-24

双曲線関数の概要を確認する（解析学基礎）｜式と曲線を把握する #4

Math

f:id:lib-arts:20210618183529p:plain

数学Cなどで取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#1〜#3では「楕円」、「放物線」、「双曲線」の方程式とその導出について取り扱いました。

#4では#3の「双曲線」に関連して「双曲線関数」について取り扱います。主に下記を参考にします。

解析学基礎/双曲線関数 - Wikibooks

以下当記事の目次になります。
1. 双曲線関数とその概要について
2. 双曲線関数を用いた双曲線の描画
3. まとめ

1. 双曲線関数とその概要について
1節では「双曲線関数」とその概要について取り扱います。まずは双曲線関数の定義から確認します。

$\displaystyle \sinh{x} = \frac{e^x-e^{-x}}{2}$
$\displaystyle \cosh{x} = \frac{e^x+e^{-x}}{2}$

上記が双曲線関数の定義ですが、sinhはハイパーボリックサイン(hyperbolic sine)、coshはハイパーボリックコサイン(hyperbolic cosine)の略を意味します。

式の定義について確認できたので、次に双曲線関数の性質について確認します。

$\displaystyle \cosh^{2}{x} - \sinh^{2}{x} = 1$ ...①
$\displaystyle \sinh{(a+b)} = \sinh{a}\cosh{b}+\cosh{a}\sinh{b}$ ...②
$\displaystyle \cosh{(a+b)} = \cosh{a}\cosh{b}+\sinh{a}\sinh{b}$ ...③
$\displaystyle \frac{d}{dx}\sinh{x} = \cosh{x}$ ...④
$\displaystyle \frac{d}{dx}\cosh{x} = \sinh{x}$ ...⑤

上記はどれも三角関数に似た性質を持つので三角関数と同様の記号が用いられています。また、①の性質より、 $(x,y) = (\cosh{t},\sinh{t})$ のように双曲線関数を用いて双曲線上の点を表すことができます。これは通常の三角関数が $(x,y) = (\cos{t},\sin{t})$ のように単位円上の点を表すことができることと対応づけておくと良いです。

双曲線関数の式定義と簡単な性質について把握できたので1節はここまでとします。

2. 双曲線関数を用いた双曲線の描画
2節では双曲線関数を用いた双曲線の描画について取り扱います。1節でも簡単に取り扱いましたが、①の式が成立することの確認や具体的に双曲線を描画することで、双曲線関数について把握できればと思います。まずは①の式が成立することを確認します。

$\displaystyle \cosh^{2}{x} - \sinh^{2}{x} = \left( \frac{e^x+e^{-x}}{2} \right)^2 - \left( \frac{e^x-e^{-x}}{2} \right)^2$
　　 $\displaystyle = \frac{e^{2x}+2e^xe{-x}+e^{-2x}}{4} - \frac{e^{2x}-2e^xe{-x}+e^{-2x}}{4}$
　　 $\displaystyle = \frac{4e^xe{-x}}{4}$
　　 $\displaystyle = \frac{4}{4}$
　　 $= 1$

上記より①の式が成立することが確認できました。

次に、 $(x,y) = (\cosh{t},\sinh{t})$ のように双曲線関数を用いて双曲線の描画を行います。ここでは概要を掴むにあたって $=-2,-1,0,1,2$ の値を計算し、グラフを描画します。

・ $t=-2$
$\displaystyle (\cosh{-2},\sinh{-2}) = (\frac{e^{-2}+e^{2}}{2},\frac{e^{-2}-e^{2}}{2})$
　　 $= (3.762195691083631, -3.6268604078470186)$

・ $t=-1$
$\displaystyle (\cosh{-1},\sinh{-1}) = (\frac{e^{-1}+e^{1}}{2},\frac{e^{-1}-e^{1}}{2})$
　　 $= (1.5430806348152437, -1.1752011936438014)$

・ $t=0$
$\displaystyle (\cosh{0},\sinh{0}) = (\frac{e^{0}+e^{0}}{2},\frac{e^{0}-e^{0}}{2})$
　　 $= (1, 0)$

・ $t=1$
$\displaystyle (\cosh{1},\sinh{1}) = (\frac{e^{1}+e^{-1}}{2},\frac{e^{1}-e^{-1}}{2})$
　　 $= (1.5430806348152437, 1.1752011936438014)$

・ $t=2$
$\displaystyle (\cosh{2},\sinh{2}) = (\frac{e^{2}+e^{-2}}{2},\frac{e^{2}-e^{-2}}{2})$
　　 $= (3.762195691083631, 3.6268604078470186)$

計算結果から $(x,y)=(1,0)$ を通り、徐々に $x$ と $y$ の値が近づくことから双曲線が描けそうだということが確認できます。

また、以下ではPythonでの描画で確認してみます。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

t1 = np.arange(-2,2.1,0.1)
t2 = np.arange(-2,3,1)

plt.plot( (np.e**(t1)+np.e**(-t1) )/2., (np.e**(t1)-np.e**(-t1))/2., color="limegreen")
plt.scatter( (np.e**(t2)+np.e**(-t2) )/2., (np.e**(t2)-np.e**(-t2))/2.)

plt.show()

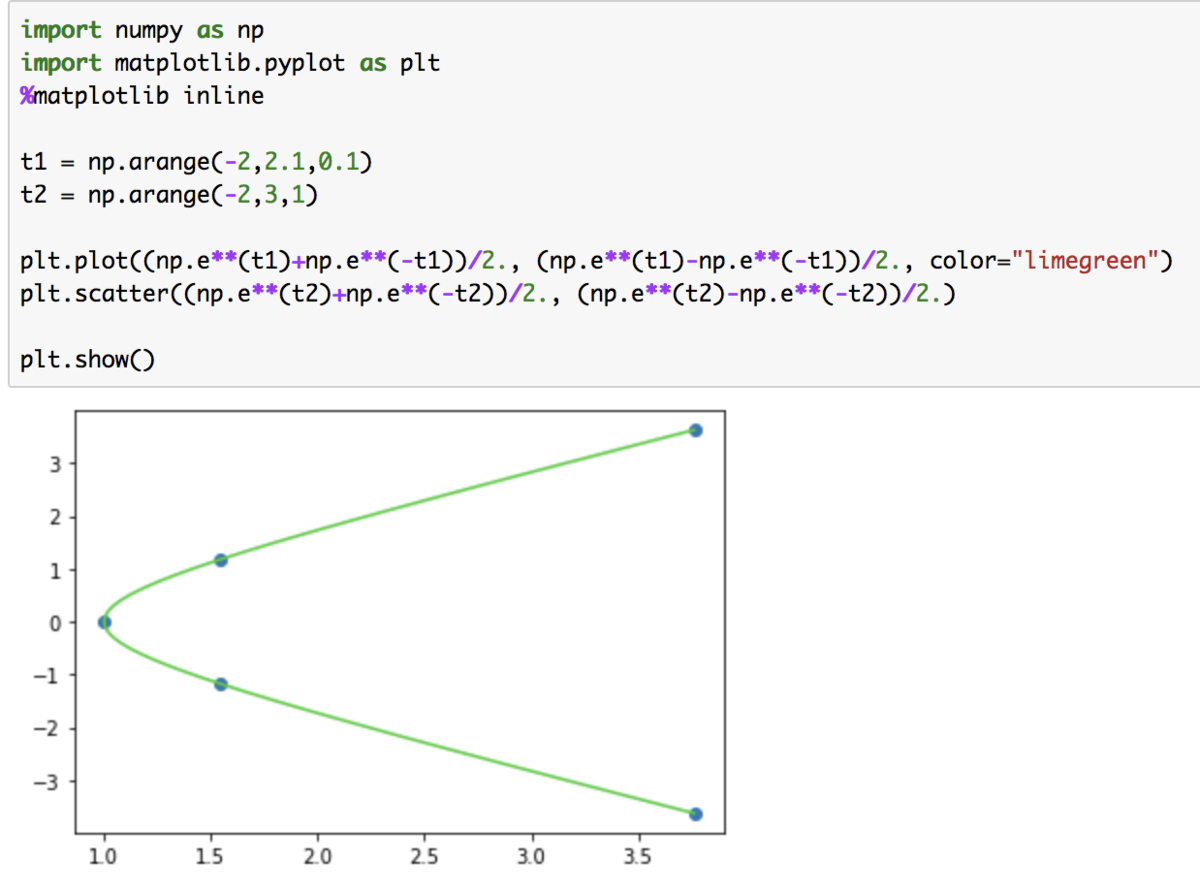
f:id:lib-arts:20210623171602p:plain

上記のように、グラフが確認できます。また、 $(x,y) = (\pm \cosh{t},\sinh{t})$ を考慮することで反対側も同時に描画できます。

f:id:lib-arts:20210623171623p:plain

上図が双曲線のグラフの描画にあたって紹介されることが多いと思います。

双曲線関数を用いた双曲線の描画について取り扱えたので2節はここまでとします。

3. まとめ
#4では解析学の基礎より双曲線関数の概要を確認しました。
#5では下記を参考に円錐曲線と離心率について取り扱います。

円錐曲線 - Wikipedia

2021-06-23

双曲線の方程式と導出｜式と曲線を把握する #3

Math

f:id:lib-arts:20210618183529p:plain

数学Cなどで取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#1では「楕円」の方程式と導出、#2では「放物線」の方程式と導出について取り扱いました。

#3では「双曲線」の方程式と導出について取り扱います。主に下記を参考に進めます。

高等学校数学C/式と曲線 - Wikibooks

以下当記事の目次になります。
1. 双曲線の方程式とその概要
2. 双曲線の方程式の導出
3. まとめ

1. 双曲線の方程式とその概要
1節では「双曲線」の方程式とその概要に関して確認します。まずは双曲線の方程式について確認します。

$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ ①
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1$ ②
（ $a$ と $b$ は正の定数）

上記が双曲線の方程式です。概要を掴むにあたって①について考えます。具体的に考える方がわかりやすいので、 $y=0$ 、 $y=1$ 、 $y=2$ を考え、これに対応する $x$ の値を計算を行うとします。

・ $y=0$ のとき
$\displaystyle \frac{x^2}{a^2} = 1$
$x^2 = a^2$
$a$ ＞ $0$ より $x = \pm a$

・ $y=1$ のとき
$\displaystyle \frac{x^2}{a^2} - \frac{1}{b^2} = 1$
$\displaystyle \frac{x^2}{a^2} = 1+\frac{1}{b^2}$
$\displaystyle \frac{x^2}{a^2} = \frac{b^2+1}{b^2}$
$\displaystyle x^2 = \frac{a^2(b^2+1)}{b^2}$
$a$ ＞ $0$ より $x = \pm \frac{\sqrt{a^2(b^2+1)}}{b}$

・ $y=2$ のとき
$\displaystyle \frac{x^2}{a^2} - \frac{4}{b^2} = 1$
$\displaystyle \frac{x^2}{a^2} = 1+\frac{4}{b^2}$
$\displaystyle \frac{x^2}{a^2} = \frac{b^2+4}{b^2}$
$\displaystyle x^2 = \frac{a^2(b^2+4)}{b^2}$
$a$ ＞ $0$ より $x = \pm \frac{\sqrt{a^2(b^2+4)}}{b}$

$y$ に具体的な数値を入れて確認しましたが、これでもまだ具体的なイメージがつかめないので $a=b=1$ を代入して値を確認することとします。

・ $y=0$ のとき
$x = \pm 1$

・ $y=1$ のとき
$x = \pm \frac{\sqrt{a^2(b^2+1)}}{b}$
　　 $= \pm \frac{\sqrt{1^2(1^2+1)}}{1}$
　　 $= \pm \sqrt{2}$

・ $y=2$ のとき
$x = \pm \frac{\sqrt{a^2(b^2+4)}}{b}$
　　 $= \pm \frac{\sqrt{1^2(1^2+4)}}{1}$
　　 $= \pm \sqrt{5}$

これより、 $\displaystyle x = \sqrt{y^2+1}$ のようなイメージを持つと良いと思います。

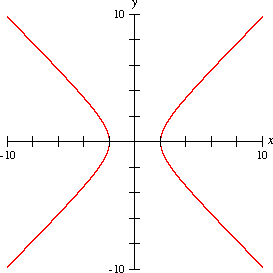
f:id:lib-arts:20210622163617p:plain

（双曲線 - Wikipedia より）
大まかな図は上記のようになります。また、双曲線には2つの漸近線が存在し、それぞれ $bx+ay=0$ 、 $bx-ay=0$ で表すことができます。

双曲線の数式とその概要について大まかに抑えられたので1節はここまでとします。

2. 双曲線の方程式の導出
2節では双曲線の方程式の導出について確認します。双曲線の定義は、「平面状にある2定点(焦点)からの距離の差が一定になるような点の集合からなる曲線」というものです。以下、2つの焦点を $(c,0)$ 、 $(-c,0)$ 、焦点からの距離の差を $2a$ とおき、双曲線の方程式を導出します。

まず、定義より下記が成立します。
$\displaystyle |\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}| = 2a$
$\displaystyle \sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2} = \pm 2a$
$\displaystyle \sqrt{(x-c)^2+y^2} = \sqrt{(x+c)^2+y^2} \pm 2a$
ここで上記の二乗を行います。
$\displaystyle (x-c)^2+y^2 = (x+c)^2+y^2 \pm 4a\sqrt{(x+c)^2+y^2} + 4a^2$
$\displaystyle ((x-c)^2+y^2)-((x+c)^2+y^2+4a^2) = \pm 4a\sqrt{(x+c)^2+y^2}$
$\displaystyle -4(a^2+cx) = \pm 4a\sqrt{(x+c)^2+y^2}$
$\displaystyle -(a^2+cx) = \pm a\sqrt{(x+c)^2+y^2}$
さらに上記の両辺を再度二乗します。
$\displaystyle (a^2+cx)^2 = a^2((x+c)^2+y^2)$
$\displaystyle a^4+2a^2cx+c^2x^2 = a^2(x^2+2cx+c^2+y^2)$
$\displaystyle a^4+2a^2cx+c^2x^2 = a^2x^2+2a^2cx+a^2c^2+a^2y^2$
$\displaystyle a^4+c^2x^2 = a^2x^2+a^2c^2+a^2y^2$
$\displaystyle (c^2-a^2)x^2-a^2y^2 = a^2c^2-a^4$
$\displaystyle (c^2-a^2)x^2-a^2y^2 = a^2(c^2-a^2)$
ここで $b^2=c^2-a^2$ と置き換えます。
$\displaystyle b^2x^2-a^2y^2 = a^2b^2$
さらにここで両辺を $a^2b^2$ で割ります。
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$
上記が楕円の方程式に一致します。

ここまでの議論で双曲線の方程式を導出することができました。ここで、 $b^2=c^2-a^2$ より $c^2=a^2+b^2$ なので、焦点は $(c,0)=(\sqrt{a^2+b^2},0)$ と $(-c,0)=(-\sqrt{a^2+b^2},0)$ となります。

ここまでで双曲線の方程式が導出できたので2節はここまでとします。

3. まとめ
#3では双曲線の方程式と導出について確認を行いました。
#4では下記を参考に解析学基礎から双曲線関数について取り扱います。

解析学基礎/双曲線関数 - Wikibooks

2021-06-22

放物線の方程式とその導出｜式と曲線を把握する #2

Math

f:id:lib-arts:20210618183529p:plain

数学Cなどで取り扱われる「式と曲線」を中心に取り扱うシリーズです。
#1では「楕円」の方程式とその導出について取り扱いました。

#2では「放物線」の方程式とその導出について取り扱います。主に下記を参考に進めます。

高等学校数学C/式と曲線 - Wikibooks

以下当記事の目次になります。
1. 放物線の方程式とその概要
2. 放物線の方程式の導出
3. まとめ

1. 放物線の方程式とその概要
1節では「放物線」の方程式とその概要に関して確認します。まずは放物線の方程式について確認します。

$x^2 = 4cy$ ①
$y^2 = 4cx$ ②

上記が放物線の方程式です。ここで二次関数を表す $y=ax^2$ は①の両辺を $4c$ で割った $\displaystyle y = \frac{1}{4c}x^2$ に対して、 $\displaystyle a = \frac{1}{4c}$ で置き換えることで $y=ax^2$ を導出できます。
二次関数に関する理解より放物線のグラフのイメージはつくと思いますので、放物線の定義からの導出について確認するのが当記事の主目的となります。導出について詳しくは2節で取り扱いますが、放物線の定義は「ある直線（準線）への距離とその直線上にない点（焦点）への距離とが等しい点の集合」というのは抑えることとします。

f:id:lib-arts:20210621192532p:plain

図にすると上記のようなイメージです。
放物線の方程式と大まかな概要についてつかめたので1節はここまでとします。

2. 放物線の方程式の導出
2節では放物線の方程式の導出について確認します。1節でも取り扱いましたが、放物線の定義は「ある直線（準線）への距離とその直線上にない点（焦点）への距離とが等しい点の集合」です。以下、焦点を $(0,c)$ 、 $y=-c$ とおき、放物線の方程式 $x^2 = 4cy$ を導出します。

まず定義より下記が成立します。
$\displaystyle \sqrt{x^2+(y-c)^2} = y-(-c)$
$\displaystyle \sqrt{x^2+(y-c)^2} = y+c$
次に上記の両辺を二乗します。
$\displaystyle x^2+(y-c)^2 = (y+c)^2$
$\displaystyle x^2+y^2+c^2-2cy = y^2+2cy+c^2$
$\displaystyle x^2-2cy = 2cy$
$\displaystyle x^2 = 4cy$
上記が放物線の方程式に一致します。

$x$ と $y$ を入れ替えて同様に考えることで $y^2 = 4cx$ も導出できます。
1節でも確認しましたが、ここで $\displaystyle a = \frac{1}{4c}$ が成立するので、 $c$ (＞ $0$ )の値が大きくなるにつれて、 $x$ の変化に伴って急激に $y$ が変化する放物線になることは抑えておくと良いかと思います。
ここまでで放物線の方程式が導出できたので2節はここまでとします。

3. まとめ
#2では楕円の方程式とその導出について確認を行いました。
#3では双曲線の方程式と導出について取り扱います。

2021-06-21

楕円の方程式とその導出｜式と曲線を把握する #1

Math

f:id:lib-arts:20210618183529p:plain

式と曲線の関係については二次関数などの多項式関数や三角関数など様々ですが、数学Cなどで取り扱われる楕円や放物線、双曲線などのテーマは概要を抑えてはいるもののになりがちではないかと思います。ということで、このシリーズでは数学Cなどで取り扱われる「式と曲線」について取り扱っていければと思います。
#1では「式と曲線」の中でも「二次曲線」の具体例で最初に出てくることが多い「楕円」の方程式とその導出について取り扱います。主に下記を参考に進めます。

高等学校数学C/式と曲線 - Wikibooks

以下当記事の目次になります。
1. 楕円の方程式とその概要
2. 楕円の方程式の導出
3. まとめ

1. 楕円の方程式とその概要
1節では「楕円」の方程式とその概要に関して確認します。まずは楕円の方程式について確認します。

$\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$ ①
（ $a$ と $b$ は正の定数）

上記が楕円の方程式です。この時 $y=0$ を考えると、 $x^2=a^2$ より、 $x = \pm a$ となります。このことは方程式①で表される楕円は $(-a,0)$ と $(a,0)$ を通ることを意味しています。また、同様に $x=0$ を考えると $y^2=b^2$ より、 $y = \pm b$ となり、方程式①の楕円は $(0,-b)$ と $(0,b)$ を通ることを意味します。

f:id:lib-arts:20210620174349p:plain

ここまでの話を元に楕円の図を描くと上記のようになるとすることができます。

楕円の方程式と大まかな概要についてつかめたので1節はここまでとします。

2. 楕円の方程式の導出

2節では楕円の方程式の導出について確認します。方程式の導出の前に楕円の定義から確認します。楕円の定義は、「平面状にある2定点(焦点とする)の距離の和が一定になるような点の集合からなる曲線」というものです。以下、2つの焦点を $(c,0)$ 、 $(-c,0)$ 、焦点からの距離の和を $2a$ とおき、楕円の方程式を導出します。

まず、定義より下記が成立します。
$\displaystyle \sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a$
$\displaystyle \sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}$
次に両辺を二乗し、整理を行います。
$\displaystyle (x-c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2$
$\displaystyle (x-c)^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2$
$\displaystyle 4a\sqrt{(x+c)^2+y^2}=4a^2+4cx$
$\displaystyle a\sqrt{(x+c)^2+y^2}=a^2+cx$
さらに上記の両辺を再度二乗します。
$\displaystyle a^2((x+c)^2+y^2)=(a^2+cx)^2$
$\displaystyle a^2(x^2+2cx+c^2+y^2)=(a^4+2a^2cx+c^2x^2)$
$\displaystyle a^2(x^2+c^2+y^2)=(a^4+c^2x^2)$
$\displaystyle (a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)$
ここで $b^2=a^2-c^2$ と置き換えます。
$\displaystyle b^2x^2+a^2y^2=a^2b^2$
さらにここで両辺を $a^2b^2$ で割ります。
$\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$
上記が楕円の方程式に一致します。

ここまでの話で楕円の方程式を導出することができました。また、 $b^2=a^2-c^2$ 、 $a$ ＞ $0$ 、 $b$ ＞ $0$ より、 $a$ ＞ $b$ を導出することもできます。
さらにここで $(c,0)=(\sqrt{a^2-b^2},0)$ と $(-c,0)=(-\sqrt{a^2-b^2},0)$ は楕円の焦点を表すことも抑えておくと良いと思います。

ここまでで楕円の方程式が導出できたので2節はここまでとします。

3. まとめ
#1では楕円の方程式とその導出について確認を行いました。
#2では放物線について取り扱います。

2021-06-20

sin、cos、tan以外の三角関数(sec、cosec、cot)｜三角関数の公式を完全に理解する #6

Math

f:id:lib-arts:20210618183529p:plain

三角関数の公式は数が多く大変なので、まとめて抑えるにあたってなるべくシンプルな導出について取り扱っていくシリーズです。
#5では「加法定理の図形的理解」について取り扱いました。

#6では $\sin$ や $\cos$ 、 $tan$ 以外の三角関数の $\sec$ 、 $cosec$ 、 $\cot$ について取り扱います。主に下記を参考にします。

三角関数 - Wikipedia

以下当記事の目次になります。
1. 直角三角形による定義
2. 単位円による定義
3. まとめ

1. 直角三角形による定義
1節では直角三角形による三角関数の定義について確認します。

f:id:lib-arts:20210619185254p:plain

( 三角関数 - Wikipedia より)
上図に対応する三角関数の定義はそれぞれ下記になります。

$\displaystyle \sin{\theta} = \frac{a}{h}$
$\displaystyle \sec{\theta} = \frac{h}{b} = \frac{1}{\cos{\theta}}$
$\displaystyle \tan{\theta} = \frac{a}{b} = \frac{\sin{\theta}}{\cos{\theta}}$
$\displaystyle \cos{\theta} = \frac{b}{h}$
$\displaystyle cosec {\theta} = \csc{\theta} = \frac{h}{a} = \frac{1}{\sin{\theta}}$
$\displaystyle \cot{\theta} = \frac{b}{a} = \frac{1}{\tan{\theta}}$

それぞれ上から正弦(sine: サイン)、正割(secant: セカント)、正接(tangent: タンジェント)、余弦(cosine: コサイン)、余割(cosecant: コセカント)、余接(cotangent: コタンジェント)と呼びます。また、 $cosec$ を $\csc$ と表記することも多いので抑えておくと良いと思います

直角三角形を用いた定義について確認できたので1節はここまでとします。

2. 単位円による定義
2節では単位円による三角関数の定義について確認します。

f:id:lib-arts:20210619190409p:plain

( 三角関数 - Wikipedia より)
上図の単位円上の点A $(x,y)$ に対応する三角関数の定義はそれぞれ下記になります。

$\displaystyle \sin{\theta} = y$
$\displaystyle \cos{\theta} = x$
$\displaystyle \tan{\theta} = \frac{y}{x}$
$\displaystyle \csc{\theta} = \frac{1}{y}$
$\displaystyle \sec{\theta} = \frac{1}{x}$
$\displaystyle \cot{\theta} = \frac{x}{y}$

この定義は $0$ ＜ $\theta$ ＜ $\displaystyle \frac{\pi}{2}$ で1節で取り扱った直角三角形の定義に一致することも抑えておくと良いと思います。

3. まとめ
#6では $\sec$ 、 $cosec$ 、 $\cot$ について取り扱いました。
#7以降も引き続き三角関数について取り扱います。

2021-06-19

ド・モアブルの定理の確認｜複素数平面を確認する #2

Math

f:id:lib-arts:20210618183529p:plain

複素数平面の基本的なトピックについて取り扱うシリーズです。
#1では概要の確認について行いました。

#2では「ド・モアブルの定理」について確認します。主に下記などを参考にします。

高等学校数学III/複素数平面 - Wikibooks

以下が目次となります。
1. 「ド・モアブルの定理」の概要
2. 「ド・モアブルの定理」の導出
3. まとめ

1. 「ド・モアブルの定理」の概要
1節では「ド・モアブルの定理」の概要について取り扱います。

$\cos{\theta}+i\sin{\theta} = \cos{n\theta}+i\sin{n\theta}$

まず、数式の確認からですが、「ド・モアブルの定理」は上記のように表します。以下、1節では具体的なイメージを掴むためにこの定理の利用例を確認します。

$z^n=a$

上記において $a$ が実数の時の $z$ に関しての $n$ 次方程式の全ての複素数解を求めることを考えます。ここで $z=r(\cos{\theta}+i\sin{\theta})$ と表せるとすると、「ド・モアブルの定理」より下記が成立します。

$z^n=r^n(\cos{\theta}+i\sin{\theta})^n$
　　 $=r^n(\cos{n\theta}+i\sin{n\theta})$

ここで実数 $a$ の絶対値は $a$ 、偏角は $0$ であることを考慮すると、 $r^n=a$ 、 $n\theta = 2k\pi$ ( $k$ は整数)となることがわかります。

$\displaystyle r = (a)^{\frac{1}{n}}$
$\displaystyle \theta = \frac{2k\pi}{n}$

よって、上記が成立するので、求める解は整数 $k$ を用いて下記のように表すことのできる数となります。

$\displaystyle z = (a)^{\frac{1}{n}} \left( \cos{\frac{2k\pi}{n}} + i\sin{\frac{2k\pi}{n}} \right)$

ここまでの内容で「ド・モアブルの定理」の数式や利用例に関して確認できたので1節はここまでとします。

2. 「ド・モアブルの定理」の導出
2節では「ド・モアブルの定理」の導出について取り扱います。基本的には加法定理を用いることで導出を行います。

$z_1 = \cos{\theta_1}+i\sin{\theta_1}$
$z_2 = \cos{\theta_2}+i\sin{\theta_2}$

上記のように $z_1$ と $z_2$ とおいた際に、 $z_1z_2$ の計算を考えます。

$z_1z_2 = (\cos{\theta_1}+i\sin{\theta_1})(\cos{\theta_2}+i\sin{\theta_2})$
　　 $= \cos{\theta_1}\cos{\theta_2}+i\cos{\theta_1}\sin{\theta_2}+i\sin{\theta_1}\cos{\theta_2}+i^2\sin{\theta_1}\sin{\theta_2}$
　　 $= (\cos{\theta_1}\cos{\theta_2}-\sin{\theta_1}\sin{\theta_2})+i(\sin{\theta_1}\cos{\theta_2}+\cos{\theta_1}\sin{\theta_2})$
　　 $=\cos{(\theta_1+\theta_2)}+i\sin{(\theta_1+\theta_2)}$

上記のように加法定理を考えることによって「ド・モアブルの定理」を導出することができます。途中で $i^2=-1$ を用いたところもポイントです。

3. まとめ
#2では「ド・モアブルの定理」について確認しました。
#3以降でも引き続き複素数平面のトピックについて取り扱います。

2021-06-18

概要と基本的な表記の確認｜複素数平面を確認する #1

Math ComplexPlane

f:id:lib-arts:20210213195311p:plain

複素数平面の基本的なトピックについて取り扱うシリーズです。複素平面と同義で専門的にはcomplex planeの訳語に複素平面とあてることが多いようですが、基本的なトピックを扱う当シリーズでは複素平面と表記することとします。
#1では概要の確認について行います。主に下記などを参考にします。

高等学校数学III/複素数平面 - Wikibooks

複素平面 - Wikipedia

以下が目次となります。
1. 複素平面の概要
2. 基本的な表記の確認
3. まとめ

1. 複素平面の概要
1節では複素平面の概要について確認します。

f:id:lib-arts:20210617195854p:plain

f:id:lib-arts:20210617195914p:plain

複素平面 - Wikipedia

上記がWikipediaの記載ですが、複素数平面は「複素数 $z=x+iy$ を直交座標 $(x, y)$ に対応させた直交座標平面のこと」とされています。

以下ではWikibooksの表記を確認していきます。

f:id:lib-arts:20210617195957p:plain

(高等学校数学III/複素数平面 - Wikibooks より)
上記が複素数平面を考える上で基本的に用いられる図です。横軸を実軸(Realの略でReとされることもある)、縦軸を虚軸(Imaginaryの略でImとされることもある)として、複素数 $z=x+iy$ を平面上で表記しています。また、 $z=x+iy$ に対して、 $z=x-iy$ を共役と呼ぶことも抑えておくと良いと思います。