2020-11-20

線形回帰処理のパフォーマンス比較①（解析解）｜Pythonにおける処理高速化をラフに考える #5

Python SpeedUp scikit-learn

f:id:lib-arts:20201113203327j:plain

このシリーズではPythonの処理高速化についてラフに取り扱っています。
#4ではリストの生成と内包表記について取り扱いました。

#5では単回帰分析の解析解を求める処理について、scikit-learnなどを中心にパフォーマンス比較を行いたいと思います。
以下、目次になります。
1. 問題設定＆サンプル数を変えてscikit-learnを実行する
2. NumPyを用いた実装との処理時間の比較
3. まとめ

1. 問題設定＆サンプル数を変えてscikit-learnを実行する
1節では問題設定と処理のパフォーマンス比較を行います。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
%matplotlib inline

np.random.seed(0)

x = np.arange(-1, 9, 0.1)
x_ = x.reshape(x.shape[0],1)
y = x*2 + 1 + np.random.normal(0, 0.1, x.shape[0])

plt.scatter(x,y)
plt.show()

f:id:lib-arts:20201120182432p:plain
問題設定としては上記のように回帰分析の問題を設定するとします。ここで、上記ではxの区間が10かつ、各サンプルの幅が0.1なので100個のサンプルを生成しています(サンプル数はx.shape[0]で確認が可能)。
まずはこちらについてscikit-learnを用いて回帰分析を計算してみます。

%%time

print(x_.shape[0])
reg = LinearRegression().fit(x_, y)

print(reg.coef_)
print(reg.intercept_)

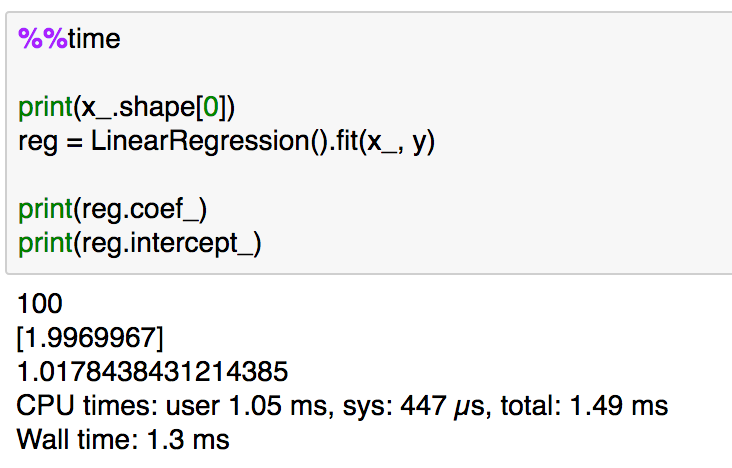
f:id:lib-arts:20201120182611p:plain

処理時間は大体1msとなっていることが確認できます。以下、サンプルを増やすとどうなるかについて実験してみます。

f:id:lib-arts:20201120182921p:plain

f:id:lib-arts:20201120182942p:plain

f:id:lib-arts:20201120183002p:plain

10倍ずつ増やして、1,000、10,000、100,000で実験した結果が上記です。少しずつ処理時間自体は増えていますが、ここまでは100サンプルと比較した際に5倍以内に収まると考えておいて良さそうです。もう少しサンプル数を増やして実験してみます。

f:id:lib-arts:20201120184338p:plain

f:id:lib-arts:20201120184440p:plain

f:id:lib-arts:20201120184457p:plain

同様に10倍ずつ増やして、1,000,000、10,000,000、100,000,000サンプルについてそれぞれ実行を行ってみました。1,000,000サンプルあたりから、サンプルの増加に比例して処理時間が伸びているとある程度考えて良さそうです(さらに10倍の10億サンプルはサンプルの生成がデフォルトだと難しかったので、1億サンプルを最大とし打ち切るものとしました)。

scikit-learnの処理の確認と、サンプルを増やしての実験について概ね確認できたので1節はここまでとします。

2. NumPyを用いた実装との処理時間の比較
2節では1節でscikit-learnを用いて行った実装を他の実装手法を用いて行ってみたいと思います。

上記の記事における実装を用いたパフォーマンス測定を行ってみたいと思います。

f:id:lib-arts:20201120185941p:plain
100サンプルの実行結果としては上記のように、scikit-learnよりも1.5〜2倍程度速い結果となりました。基本的には処理時間の増加の度合いはscikit-learnを用いた際とそれほど変わらなかったため、以下1億サンプルの場合のみをご紹介します。

f:id:lib-arts:20201120190012p:plain

1億サンプルを用いた処理としては、上記のようになりました。1節のscikit-learnを用いた実装と比較すると5倍程度高速化が実現されています。サンプル数はそれほど関係なくNumPyを用いて数式ベースで実装した方が数倍程度速いので、高速化が実現できた理由としてはscikit-learnだとロバストに書かれた処理(エラーチェックなど)を省略しているので、少しばかり高速化できたと考えて良いのではと思います。

3. まとめ
#5では回帰分析に関連して、scikit-learnのlinear_modelと数式をNumPyで実装するパターンで解析解の計算にあたってのパフォーマンス比較を行ってみました。数式をNumPyベースで実装する方が数倍程度速くなったので、理論を理解するメリットについてもわずかながら提示できたのではないかと思います。
引き続き#6では勾配法(Gradient Descent)を用いた回帰モデルについて取り扱っていきます。

2020-11-20

自動微分(Automatic differentiation)の概要｜微分をプログラミングする #1

Math Programming

f:id:lib-arts:20201120163314p:plain

近年の深層学習(DeepLearning)の発展により、プログラミングにおける微分の取り扱いは重要度を増しています。基本的な意味での微分のプログラミング的取り扱いとしてイメージとして挙がりやすいのは、微分した数式を用いる「数式微分(Symbolic differentiation)」と、数値的に関数から近似を行う「数値微分(Numerical differentiation)」ですが、近年では誤差逆伝播における高速化などの必要性から「自動微分(Automatic differentiation)」についても用いられることが多いです。
これらを受け、当シリーズでは「微分をプログラミングする」をテーマに、基本的な内容から発展的な話題まで取り扱っていければと思います。#1では誤差逆伝播などにも用いられている「自動微分(Automatic differentiation)」の概要について確認していきます。
以下、目次になります。
1. 自動微分(Automatic differentiation)の概要
2. 具体例で確認する自動微分
3. まとめ

1. 自動微分(Automatic differentiation)の概要
1節では「自動微分(Automatic differentiation)の概要」について確認します。最初から詳しく確認するのは大変なので、Wikipediaを元に概要をざっくり掴むことを目的とします(https://ja.wikipedia.org/wiki/自動微分)。

f:id:lib-arts:20201120163707p:plain

まず、上記が冒頭の解説ですが、「複雑な関数を基本的な演算の組み合わせとみなし、連鎖律を繰り返し利用することで微分を実現する考え方」とざっくり掴んでおけば十分だと思います。また、ここで比較として提示されている数式微分と数値微分については、「数式微分は手計算をベースに導出した導関数を元にした実装(高校レベルのイメージ)」、「数値微分はコンピュータを用いて差分処理を行うことで実現する実装(工学部3〜4年が取り扱うイメージ)」ということで、把握しておけば良いかと思います。

f:id:lib-arts:20201120164223p:plain

また、自動微分の意義としては上記のように、「解析的な視点が必要な数式微分」と「離散化や桁落ちによる精度が低下する可能性のある数値微分」のどちらにおいても難しい、「高次の微分係数を求める問題」や「入力変数の多い関数の偏微分の計算」などの問題を解決することが挙げられています。

f:id:lib-arts:20201120164618p:plain

自動微分の仕組みとしては上記のように連鎖律(合成関数の微分)を用いた微分の分解を基本原理としています。誤差逆伝播もこちらがベースなので、同様なイメージを持っておくと良いかと思います。ここで、2種類に分けられていますが、連鎖律の右辺において右から計算するか左から計算するかの違いなので、あまり難しく考えないで大丈夫だと思います。

大体の概要は掴めたかと思うので1節はここまでとし、続く2節で具体例を元に自動微分を確認していければと思います。

2. 具体例で確認する自動微分
2節では自動微分について具体例を元に確認していきます。Wikipediaの例を元に $f(x_1, x_2) = x_1 x_2 + \sin{x_1}$ を自動微分的に考えてみます。

$\displaystyle \frac{\partial f}{\partial x_1} = x_2 + \cos{x_1}$

$\displaystyle \frac{\partial f}{\partial x_2} = x_1$

まず、通常の偏微分だと上記のように計算できますが、数式が高次になるとこのような偏微分をベースにすると大変なので、自動微分的な考え方(ここではボトムアップ型の自動微分を考えます)を導入します。

f:id:lib-arts:20201120165718p:plain

f:id:lib-arts:20201120165735p:plain

自動微分をこの問題に適用すると上記のように、中間出力を $w_1$ 〜 $w_5$ で表すことで(Operations to compute value)、連鎖律の適用を行なっています(Operations to compute derivative)。

f:id:lib-arts:20201120163314p:plain

ここで行なった計算を図式化したのが上記です。

f:id:lib-arts:20201120170200p:plain

また、改めて数式で表すと上記のようになります。

$\displaystyle \dot{w}_5 = \frac{\partial f}{\partial x_1} = x_2 + \cos{x_1}$

Wikipediaの記載では少しわかりづらいですが、上記の対応があることは抑えておきましょう。具体例を元に大まかな流れは確認できましたので2節はここまでとします。

3. まとめ
#1では自動微分(Automatic differentiation)の概要について確認を行いました。
続く#2ではWikipediaについてもう少し確認しつつ、論文などを参照しながら応用文脈における自動微分について確認していければと思います。

2020-11-19

リストの生成と内包表記｜Pythonにおける処理高速化をラフに考える #4

Python SpeedUp

f:id:lib-arts:20201113203327j:plain

このシリーズではPythonの処理高速化についてラフに取り扱っています。
#3ではPandasとmapについて取り扱いました。

#4ではリストの生成と内包表記について取り扱います。
以下、目次になります。
1. 内包表記の構文とパフォーマンスの比較
2. timeitを用いた統計による比較
3. まとめ

1. 内包表記の構文とパフォーマンスの比較
1節では内包表記の構文と、パフォーマンスの比較について確認を行います。

[iの式 for i in リスト]

まず、内包表記の構文ですが、上記のようにリストを作成します。

[i*2 for i in range(10)]

たとえば、偶数を0から10個並べたリストだと上記のように実装できます。

大体の構文については把握できたと思うので、具体的に実行しつつパフォーマンスを比較してみましょう。

%%time

a1 = [i*2 for i in range(100000)]
print(a1[:10])

f:id:lib-arts:20201119211707p:plain

偶数のリストを上記のように内包表記を用いて作成を行っています。

次に、for文を用いてappendした実装について確認してみます。

%%time

a2 = list()
for i in range(100000):
a2.append(i*2)
print(a1[:10])

f:id:lib-arts:20201119212054p:plain

内包表記の記載と同じ結果が得られていますが、処理時間としては約2倍となっていることが確認できます。

#2や#3でご紹介したmapについても合わせて比較してみましょう。

%%time

a3 = list(map(lambda x: x*2, range(100000)))
print(a3[:10])

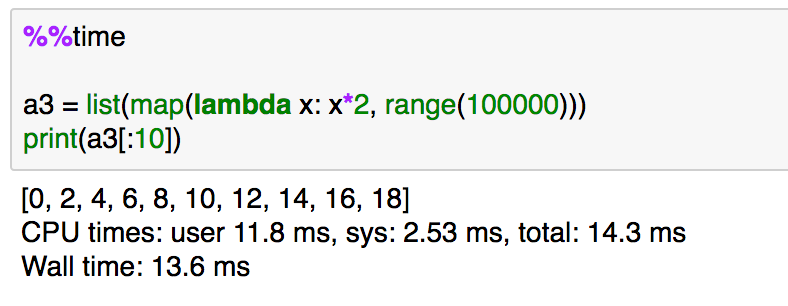
f:id:lib-arts:20201119212328p:plain

上記のように、内包表記よりは遅く、appendを利用したパターンよりは高速であることが確認できます。

ここまで3通りのリストの作成について確認してきましたが、内包表記で作成した場合が一番パフォーマンスがよくなりそうです。とはいえ、処理時間が0.01秒くらいではあるので、誤差についても気になるところです。そこで、2節では%%timeではなく%%timeitを用いることで、処理の実行時間を統計的な視点で確認します。

2. timeitを用いた統計による比較
1節では内包表記を用いたリストの生成にあたっての処理速度を他の2つの方法と比較を行いましたが、2節では%%timeではなく%%timeitを用いることで統計的に実行時間を確認してみれればと思います。実行コードは基本的に同じで、%%timeを%%timeitに変えているだけなので、キャプチャだけのご紹介とします。

f:id:lib-arts:20201119212841p:plain

結果としては上記のように、1節で取り扱ったのとほぼ同様な結果ですが、若干appendを用いた実装が高速であることが読み取れます。1節で用いた%%timeでは1回の実行結果である一方で、2節で用いた%%timeitは複数回の実行結果の平均と標準偏差を計算しています。

f:id:lib-arts:20201119215127p:plain

runsやloopsについては上記のように引数を制御することも可能です。関連のドキュメントがいまいち読み取りづらく一旦詳しくまでは確認していませんが、rについて1を入れた場合は標準偏差が0になるということは確認できました。

3. まとめ
#4では内包表記を用いたリストの生成のパフォーマンスの確認と、timeitを用いた複数回実行の結果について確認しました。
続く#5以降では回帰分析の処理のパフォーマンスの確認を行います。

2020-11-19

ハミルトニアンとエネルギー保存則｜オムニバス形式で確認する解析力学 #1

Physics AnalyticalMechanics

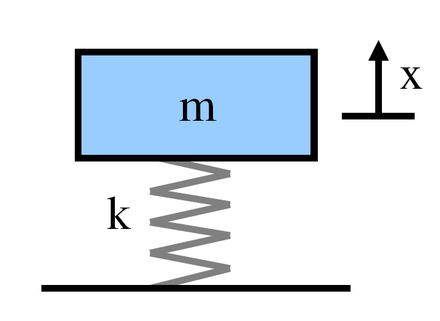
f:id:lib-arts:20201119191424p:plain

時折、解析力学的な話題が上がってくるので、必要に応じてまとめておければということで、オムニバス形式で解析力学について確認していきます。
#1では近年Hamiltonian Monte Carlo法としてMCMCサンプリングで用いられる、ハミルトニアンについて、解析力学の視点から簡単に確認できればと思います。この記事では高校物理のバネの単振動の問題において、運動量 $p$ とハミルトニアン $H(p,x)$ を導入した際のエネルギー保存則について確認していきます。
以下目次になります。
1. 問題設定と運動方程式について
2. エネルギーの保存則と等エネルギー曲線について
3. まとめ

1. 問題設定と運動方程式について
1節では問題設定と運動方程式について確認します。単振動の問題なので、運動方程式は

$F=ma=-kx$

となります。この式は、時刻 $t$ の変位を $x(t)$ とした上で、

$m \ddot{x}(t) = -kx(t)$

のように表すこともできます。この際に $x$ の上のドットは微分を表しており、加速度の $a(t)$ は変位 $x(t)$ の二階微分であることを意味しています。また、速度 $v(t)$ は変位 $x(t)$ の一階微分なので、 $v(t) = \dot{x}(t)$ のように表すことができます。

$v(t) = \dot{x}(t)$
$a(t) = \ddot{x}(t)$

すなわち、上記が成立します。

また、ここで運動量 $p(t)$ についても導入を行います。

$p(t) = mv(t) = m \dot{x}(t)$

運動量は上記のように質量と速度の積として表すことが可能です。

単振動の問題設定や運動方程式の概要については概ねご紹介できたかと思いますので1節はここまでとします。

2. エネルギーの保存則と等エネルギー曲線について
2節ではエネルギーの保存則と等エネルギー曲線について取り扱います。まず、単振動の問題においてエネルギー保存則として下記が成立するというのは高校物理のトピックです。

$\displaystyle \frac{1}{2} mv(t)^2 + \frac{1}{2}kx(t)^2 = Const.$

この式の左辺の速度を運動量に変換すると下記のようになります。

$\displaystyle \frac{1}{2} mv(t)^2 + \frac{1}{2}kx(t)^2 = \frac{1}{2m} p(t)^2 + \frac{1}{2}kx(t)^2$

上記を元にハミルトニアン $H(p,x)$ を下記のように定義します。

$\displaystyle H(p,x) = \frac{1}{2m} p(t)^2 + \frac{1}{2}kx(t)^2$

ここで運動量と変位の時間微分は運動方程式を用いて下記のようにハミルトニアンの偏微分として表記できます。

$\displaystyle \dot{p}(t) = m \ddot{x}(t) = -kx(t) = -\frac{\partial H}{\partial x}$
$\displaystyle \dot{x}(t) = \frac{m \dot{x}(t)}{m} = \frac{p(t)}{m} = \frac{\partial H}{\partial p}$

次にハミルトニアンの時間微分を考えてみます。

$\displaystyle \frac{\partial H}{\partial t} = \frac{\partial H}{\partial p}\frac{dp}{dt} + \frac{\partial H}{\partial x}\frac{dx}{dt} = -\frac{\partial H}{\partial p}\frac{\partial H}{\partial x} + \frac{\partial H}{\partial x}\frac{\partial H}{\partial p} = 0$

上記より、ハミルトニアンは時間によって一定であることが確認できます。

$\displaystyle \frac{1}{2} mv(t)^2 + \frac{1}{2}kx(t)^2 = Const.$

また、エネルギー保存則の式である上記を $x(t)$ と $v(t)$ について見た際に、楕円の方程式である $\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$ の形に整理できることから、 $x(t)$ と $v(t)$ をそれぞれx軸、y軸と考えた際に楕円曲線を描くということがここでわかります。
この曲線のことを等エネルギー曲線と呼び、この曲線は初期値 $x(0)$ と $v(0)$ に依存して楕円軌道を描きます。

3. まとめ
#1では単振動問題において解析力学的な視点からハミルトニアンの導入やエネルギー保存則について確認しました。問題自体は高校物理のレベルですが、運動量やハミルトニアンの導入自体はもう少し高度なトピックなので式変形には慣れておきたいところです。

2020-11-19

Pandasとmap｜Pythonにおける処理高速化をラフに考える #3

Python SpeedUp Pandas

f:id:lib-arts:20201113203327j:plain

このシリーズではPythonの処理高速化についてラフに取り扱っています。
#2ではmapと繰り返し文(for)について簡単に取り扱いました。

#3ではPandasとmapについて取り扱います。
以下、目次になります。
1. mapを用いたPandasのカラムの置換
2. map、lambdaを用いた処理
3. まとめ

1. mapを用いたPandasのカラムの置換
1節ではmapを用いたPandasのカラムの置換について行います。まず、データフレームを用意する必要があるので、scikit-learnにプリインの"iris"を用いることにします。下記を実行してください。

import pandas as pd
from sklearn.datasets import load_iris

iris = load_iris()
iris_data = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_data["target"] = iris.target

f:id:lib-arts:20201119141837p:plain

実行結果にはいくつか内容確認のためのコマンドを入れておきましたので、気になる方は利用して見てください(本題とは違うのでコードは記載しませんでした)。

さて、上記でロードした"iris"を元に目的変数の"target"の置換処理を行ってみようと思います。まずはfor文とif文を組み合わせた基本的なプログラミングとして実装してみます。

%%time

iris = load_iris()
iris_data = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_data["target"] = iris.target

for i in range(iris_data.shape[0]):
if iris_data['target'][i]==0:
iris_data.loc[i, 'target']='setosa'
elif iris_data['target'][i]==1:
iris_data.loc[i, 'target']='versicolor'
elif iris_data['target'][i]==2:
iris_data.loc[i, 'target']='virginica'

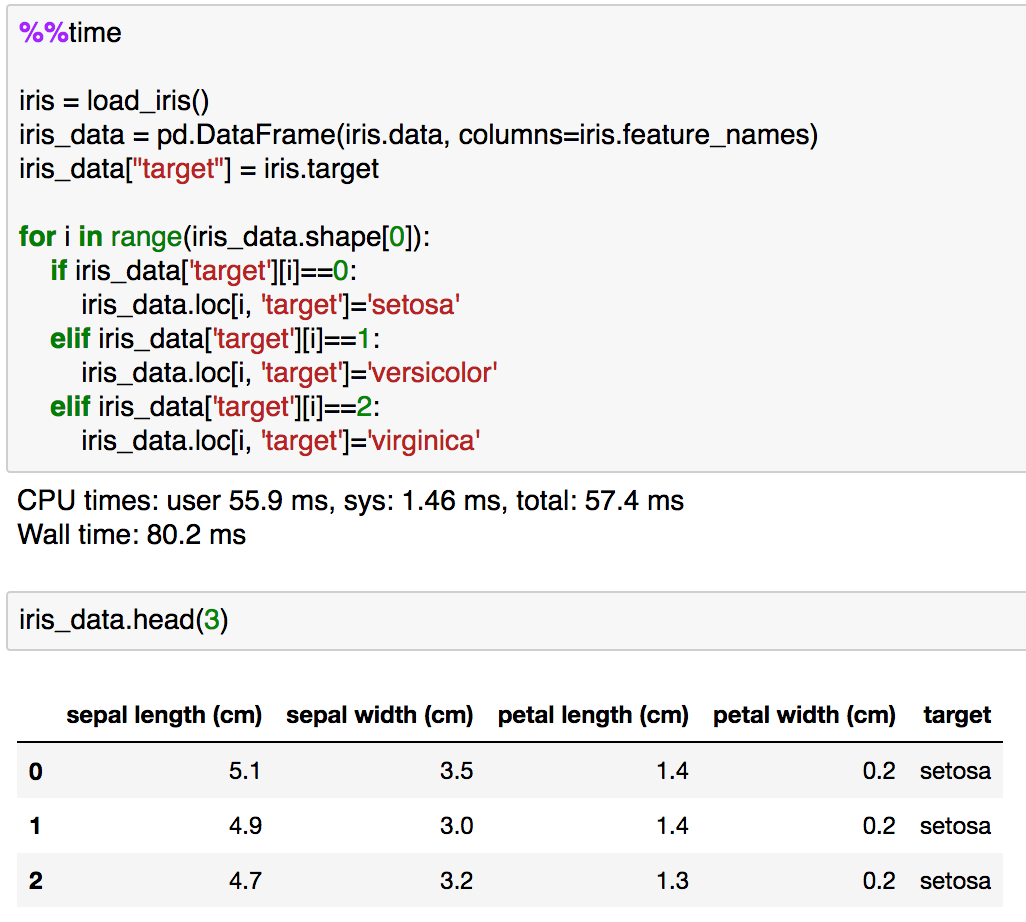
f:id:lib-arts:20201119144722p:plain
実行結果では"target"がインデックスからカテゴリ名に置き換わっているのが確認できるかと思います。ちなみにこの際に"loc"を用いているのは、そのまま代入しようとすると"SettingWithCopyWarning"が生じたためです。この辺はPandasの仕様上の問題でそのうち変わる可能性もあるので単に"Warning"が出ないようにしただけだとご理解いただけたらと思います。
for文とif文の処理が確認できたので、次はmapを用いた置換処理を実行してみます。Pandasのメソッドとしてのmapを用いた処理では辞書型を与えることで置換処理が可能なのでそちらを用いるものとします。

%%time

iris = load_iris()
iris_data = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_data["target"] = iris.target

iris_data['target'] = iris_data['target'].map({0: 'setosa', 1: 'versicolor', 2: 'virginica'})

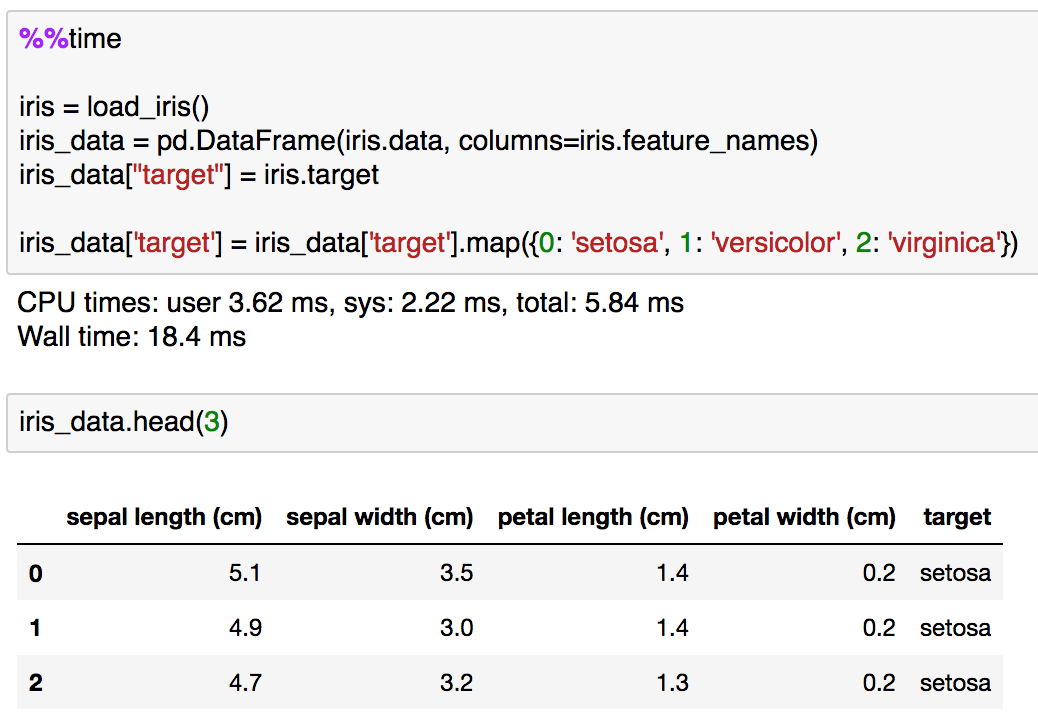
f:id:lib-arts:20201119144652p:plain
実行結果は同じですが、処理速度がかなり高速化されており、15分の1程度で実行が終了しています。高速化の度合いについてはあまりあてにしない方が良さそうですが、ある程度このように記載する方が高速化すると把握しておく分には問題なさそうです。

Pandasの形式におけるmapを用いた置換処理については簡単に確認ができたので、1節はここまでとします。

2. map、lambdaを用いた処理
1節ではmapに辞書型のオブジェクトを与えることで置換処理を記述しましたが、2節ではmap、lambdaを用いて処理を記述してみます。以下、"petal width (cm)"のカラムに値を加える処理について取り扱ってみます。

%%time

iris = load_iris()
iris_data = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_data["target"] = iris.target

for i in range(iris_data.shape[0]):
iris_data.loc[i, 'petal width (cm)'] += 1

f:id:lib-arts:20201119145321p:plain

まず、for文を用いた処理の実行結果は上記のようになります。1節の置換処理と大体同様の処理時間であることが確認できます。

次にmapとlambdaを用いて同様の処理を記述してみます。

%%time

iris = load_iris()
iris_data = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_data["target"] = iris.target

iris_data["petal width (cm)"] = iris_data["petal width (cm)"].map(lambda x: x+2)

f:id:lib-arts:20201119145627p:plain

実行結果は上記のようになります。1節と同様、15分の1程度の処理時間であることが確認できます。

3. まとめ
#3ではPandasのデータフレームにmapやlambdaを適用した例について確認を行いました。今回の例では15倍ほどの差になりましたが、数字そのものよりもある程度高速化したという理解で一旦は良いのではと思います。
#4ではリストの生成と内包表記について確認します。

2020-11-18

mapと繰り返し文｜Pythonにおける処理高速化をラフに考える #2

Python SpeedUp

f:id:lib-arts:20201113203327j:plain

このシリーズではPythonの処理高速化についてラフに取り扱っています。
#1では「%%time」を用いたパフォーマンス測定と、NumPyを用いた簡単な高速化について確認しました。

#2ではmapと繰り返し文(for)について簡単に取り扱います。
以下、目次になります。
1. Pythonの組み込み関数mapについて
2. mapを用いた高速化について
3. まとめ

1. Pythonの組み込み関数mapについて
1節ではPythonの組み込み関数のmapの概要について簡単に確認します。

f:id:lib-arts:20201118213122p:plain

組み込み関数 — Python 3.9.0 ドキュメント

上記の記載では、mapは関数(function)と配列(iterable)を引数に取るとされています。処理については2節で取り扱いますが、関数(function)の処理を配列(iterable)に対して実行するという流れです。これによって、for文の内部で記述するような処理をmapを用いて記載することが可能になります。また、この際に関数にlambdaを用いた無名関数を用いてシンプルに記述するなどの記載例もあります。

mapの簡単な概要はつかめたので1節はここまでとします。

2. mapを用いた高速化について
2節ではmapを用いた高速化について簡単に確認します。

%%time

for i in range(20000):
a = 1
while a<10000:
a += 1
if i%5000==0:
print(a)

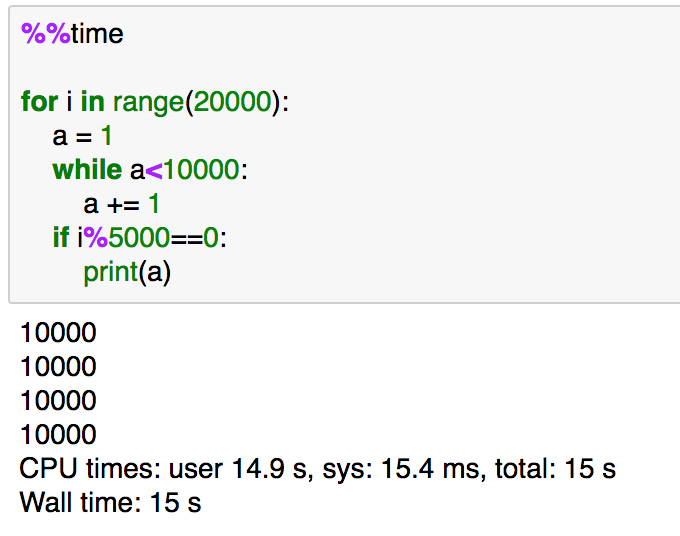
f:id:lib-arts:20201118214043p:plain

上記の処理をmapで置き換えるとします。下記を実行してみましょう。

%%time

import numpy as np
import pandas as pd

def calc_experiment(x):
a=int(x)
while a < 10000:
a += 1
return a

b = np.ones([20000], dtype=np.int)
x = map(calc_experiment, b)

i=0
for z in x:
if i%5000==0:
print(z)

i+=1

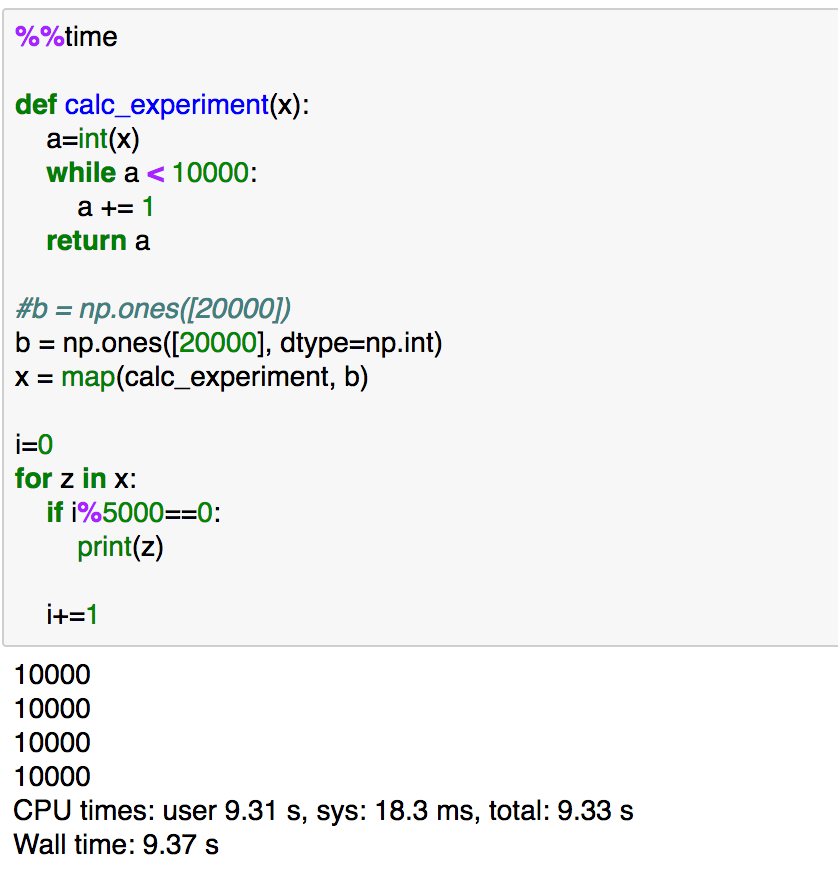
f:id:lib-arts:20201118214427p:plain

実行速度としては、上記のように少しだけ高速化が実現できています。また、mapはnextを用いて下記のように記述することもできます。

%%time

def calc_experiment(x):
a=int(x)
while a < 10000:
a += 1
return a

b = np.ones([20000], dtype=np.int)
x = map(calc_experiment, b)

for i in range(b.shape[0]):
z = next(x)
if i%5000==0:
print(z)

f:id:lib-arts:20201118214755p:plain

こちらの方が処理としては記述しやすいかもしれません。lambdaを使った例も確認できればということで、もう一例確認してみましょう。

%%time

judges = list()
for i in range(10000000):
judge = ""
if i%2==0:
judge="even"
else:
judge="odd"
judges.append(judge)

print(judges[:10])

f:id:lib-arts:20201118221424p:plain

上記をmapとlambdaを用いて記述すると下記のようになります。

%%time

a = range(10000000)
a2 = map(lambda x: 'even' if x % 2 == 0 else 'odd', a)

judges = list(a2)
print(judges[:10])

f:id:lib-arts:20201118221454p:plain

高速化としては、処理速度が2倍ほどになっていることが確認できます。また、処理の記述をシンプルに行えているというのもあります。

3. まとめ
#2では繰り返し文をmapで表現するというのを取り扱いました。今回の例では大体が1.5倍〜2倍の高速化になりましたが、高速化については他の例も確認しつつ改めて議論できればと思います。また、関連でlambdaの記法についても取り扱いました。
#3では今回取り扱ったmapやlambdaをPandasの形式に対して適用してみようと思います。

2020-11-18

Liberal Artsに基づく21世紀型民主主義の実現にあたって｜Liberal Artsを考える #2

LiberalArts Democracy economy Politics Society

f:id:lib-arts:20201118194912p:plain

21世紀は非常に難しい時代です。これまでの人類の歴史は発展の歴史として見ることもできますが、18〜19世紀の産業革命から20世紀を通して「需要」と「供給」の力関係が変わったというのが考察の難しいポイントだと思います。「需要」が大きく「供給」があれば売れるという時代から、「供給」が多過ぎて「需要」が追い付かないという時代に変わってきた、というのが昨今の流れではないでしょうか。
しかし、世の中の関心はいまだに「供給」に向いている印象で、結果デフレが続いていると見て良いのではないでしょうか。デフレ、インフレについては難しい解説が多いですが、単に「需要」＞「供給」がインフレ、「需要」＜「供給」がデフレと考えておけば理解しやすいです。

さて、デフレが続く状況ですが、社会全体が豊かになったはずが、上記で論じたように「自由に選べない」人が増えていないでしょうか。とはいえ、「結果平等」を求めてしまっては社会の停滞にもつながりかねませんし、それを懸念する方も多くおられると思います。

当記事ではこれらの背景を踏まえ、解決策として「Liberal Artsに基づく21世紀型民主主義の実現」を提唱したいと思います。解決策のポイントとしては、「社会」を「経済」ではなく一段高度な「政治」の視点から見るということですが、「政治」の取り扱いは非常に難しいです。「経済」は「売上」や「利益」などでKGIを数値化できますが、「政治」はそもそも「KGIを何にするか」から論じなくてはなりません。「王による圧政」、「エリート主義」、「衆愚政治」など、様々な失敗例があります。
「中間層(ラフに上位20％〜80％を指すものとします)が力を持った状態における、Liberal Artsに基づく民主主義」が「政治」の運用においては最も正統ではないかという考え方に当記事は基づき、21世紀型の民主主義の実現について論じてみようと思います。
以下、目次になります。
1. 民主主義が機能する条件とは
2. なぜ中間層が力を持つ必要があるのか
3. ケインズ経済学による中間層の強化
4. Liberal Artsに基づく民主主義の運用とは
5. まとめ

1. 民主主義が機能する条件とは
1節では民主主義が機能する条件について論じてみようと思います。簡単に列挙してみます。

・有権者の大半(8割以上)がラフなレベルで政策の概要を正確に把握している(詳細を把握することよりも概要を正しく理解する方が重要)
・多様な有権者の意見を反映する制度であること(小選挙区制は少し疑問符)

上記のように列挙しましたが、「概要を正確に把握する」というのが特に重要だと思います。「1人1票」という大原則があるわけですから、いわゆる「知識マウント」のような議論はNGで、「運転免許のように30分〜1時間講習を受ければある程度わかるような粒度」で多数が理解するという状況が望ましいです。
また、「多様な意見を反映する制度であること」、ですが、現行の小選挙区制は「組織票」に脆弱であり、もう少しロバストな制度の方が望ましいかと思います。そういう意味ではかつての「中選挙区制」の方が権力が集中し過ぎず、良い制度だったかもしれません。

さて、二つの条件について見てきましたが、現状「政治」が難しく見えるものになっており、SNSではデマが飛び交ったりすることでさらに正確な情報へアクセスすることが難しくなっています。また、非正規労働などの増加により中間層に余裕がなくなっているというのもよくない傾向で、こちらについては続く2節で考えたいと思います。

2. なぜ中間層が力を持つ必要があるのか
1節では「民主主義が機能する条件」として二つまとめましたが、「有権者の大半(8割以上)が正しく政策の概要について理解する」というのはそれほど簡単なことではありません。投票率についても話題になりますが、興味・関心以前の問題として「内容がよくわからない」というのがあるのではないでしょうか。
ここで注意が必要なのが「正しく理解する」については「選抜試験」ではなく「通過儀礼」的なものであるべきであるということです。そのため、個々人の才覚に可能な限り依存せずに全員が政策に対して同様な「事実認識」を持てるかというのが非常に重要になります。ここで同様な「意見」ではなく「事実認識」としているのも重要な点です。「意見」は多様であっても良いですが、「事実認識」はある程度揃えないと「デマ」が飛び交う原因にもなり「集団における意思決定」は非常に困難になります。
ですが、この「事実認識」をある程度揃えるというのはかなり難しいです。ここで重要になるのが「中間層が力を持ち、豊かである」ということです。中間層がある程度豊かに暮らせているか、それとも周囲にとってマイナスになっても自分のプラスを追求するか、によって多数派の「事実認識」が異なってきます。人はある程度余裕がある時であれば客観的に考えられる話題でも、余裕がなければ「事実認識」に歪みが出ることが多いです。
このように中間層がある程度豊かであれば、「有権者の大半が正しい事実認識に基づいて意思決定」ができるようになると思います。

上記では古代ローマにおけるポエニ戦争を取り扱っていますが、この当時のローマが強かったのは「市民」を中心とした統治に一因があったと考えて良いと思います。

それでは、中間層を豊かにするにはどのようにするのが良いでしょうか。3節ではこの鍵になる考え方としてケインズ経済学について考えます。

3. ケインズ経済学による中間層の強化
経済学は様々な流派があり、詳しく見ていくと大変ですが、概ね下記の3つに分けられるかと思います(出典などはなくいい加減でラフな理解ですが、何も知らないよりは8割わかる方が良いという意味での分類です)。

・古典派経済学(ミクロ経済、セイ、フリードマン、新自由主義、金融政策)
・ケインズ経済学(マクロ経済、有効需要、財政政策)
・マルクス経済学

よく見かけるのが、「フリードマン経済学」と「マルクス経済学」の対比で、「資本主義」と「社会主義」の比較としての議論ですが、これはそれほど有意義な議論にはならないように見ています。「マルクス」はどうしてもかつてのソ連(スターリン)などのイメージも強く、あまり論じない方が良いのではと思います(マルクスについては学術的な論考としては触れる方が望ましいですが、一般向けの解説としては望ましくなさそうです)。
なので、現代社会においては「需要」にフォーカスする「ケインズ経済学」と「供給」にフォーカスする「フリードマン経済学」の対比で考えると良いのではと思います。

上記の5節で論じたように、「ケインズ経済学」の方が基本的に運用しやすい経済学で、「(有効)需要」を中心に考えることで「実体経済」を中心に世の中が周り、結果「中間層」の強化になると思います。この「ケインズ経済学」は「大恐慌」の頃の1930年頃〜1970年代まで世界の中心であり、高度経済成長〜Japan as No.1までの繁栄を実現した、日本と非常に相性の良い経済学だったと思います。ソ連のゴルバチョフが来日時に「日本は最も成功した社会主義国である」と述べたのが関連で非常に興味深い話です。ケインズ経済学は「資本主義」をベースにした考え方でありながら対比される考え方である「社会主義」的な理想も同時に実現できるという非常にロバストな経済学と考えて良いのではないかと思います。（ここでゴルバチョフが言及した「社会主義」はイデオロギーというよりは、中間層が豊かに暮らせる社会をイメージしていたのではないかと思います; https://ja.wikipedia.org/wiki/日本型社会主義）
ゴルバチョフ来日頃の日本社会は一種の理想形であり、これを実現した当時の政治家(特に基盤を構築した1960〜1970年代の政治家)や官僚たちはもっと評価されるべきなのかもしれません。

4. Liberal Artsに基づく21世紀型民主主義の運用とは
3節では「ケインズ経済学による中間層の強化」について論じました。3節では「ケインズ経済学」の良い点を中心に論じましたが、もちろん「ケインズ経済学」も万能ではなく、考え方だけでなく運用も重要です。この辺も含め、豊かになった中間層がどのように「集団的な意思決定」を行っていけば日本国における社会や、国際社会にプラスになるのかを議論せねばなりません。
特に、「環境問題」が「有効需要」をベースとする「ケインズ経済学」における課題になりそうで、「持続可能性」の議論がどうしても必要不可欠になります。「ケインズ経済学」は運用しやすいマクロ経済学である一方で、「持続可能性」はその対極に近いところに存在するのではと思います。「適切な自省」が求められる訳ですが、なかなか多くの人がそれに気づくのは大変かもしれません。
そこで考え方として「Liberal Arts」を基盤にする必要があると、ここでは主張したいと思います。

#1でも論じましたが、大局観を持つには特定の分野だけではなく、様々な分野の知見を組み合わせる必要があり、その基盤として「Liberal Arts」が役に立ちます。
「持続可能性」に限らず、様々な複雑な問題が現代社会では生じますが、「Liberal Arts」的な見方は問題が複雑になればなるほど必要になることを強調しておきたいと思います。

5. まとめ
#2では「Liberal Artsをベースとする21世紀型の民主主義の実現」について論じました。「民主主義」において重要なのが「構成員1人1人が正しい事実認識に基づいて自由に意思決定をする」ということです。また、「1人1人が正しく事実認識をする」上で最も重要なのが、中間層がある程度豊かに暮らせる社会を作るということです。

・ケインズ経済学をベースとする中間層の強化
・Liberal Artsを元にした大局的思考、判断の強化
・持続可能性を実現しつつ豊かな社会を享受する民主主義の実現

上記に基づく社会の実現を考えるのは少し理想論かもしれませんが、こちらが21世紀における望ましい民主主義の運用ではないかというのが筆者の見解です。